Тема: «Производная функции, ее применение к приближенным вычислениям и исследованию функций».
Знания:
- определение дифференцируемости функции;
- приращение функции и приращение аргумента;
- определение производной функции, ее физический и геометрический смыслы;
- правила дифференцирования и таблица производных.
Умения:
- находить производные простых и сложных функций;
- решать задачи с учетом профессиональной направленности;
- применять производные к исследованию функций.
Задание 1.
Найти производные следующих функций.
а) 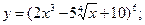 б)
б) 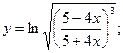 в)
в) 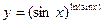
г); 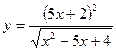 ; д)
; д) 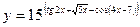 .
.
Решение.
а) 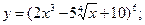
Рассмотрим сложную функцию. Для нахождения ее производной воспользуемся формулой 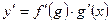 . Внешней функцией является степенная функция, а внутренней – функции находящиеся в скобках.
. Внешней функцией является степенная функция, а внутренней – функции находящиеся в скобках.
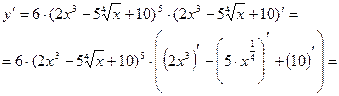
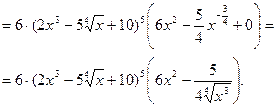
б) 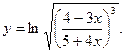
Предварительно преобразуем данную функцию, учитывая свойства степеней и логарифмов:
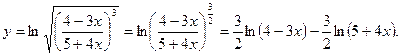
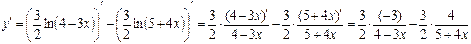
в) 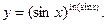
Поскольку основание и показатель степени являются функциями от 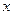 , то применяем логарифмическое дифференцирование. Логарифмируем левую и правую части:
, то применяем логарифмическое дифференцирование. Логарифмируем левую и правую части:
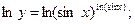
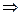
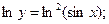
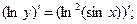
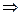
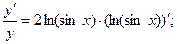
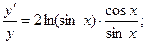
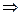
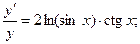
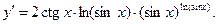
г) 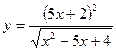
Для нахождения производной данной функции воспользуемся формулой
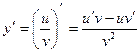
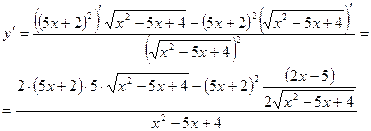
д) 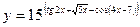
Рассмотрим сложную функцию. Для нахождения ее производной воспользуемся формулой 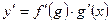 . Внешней функцией является показательная функция, а внутренней – функции находящиеся в скобках в степени.
. Внешней функцией является показательная функция, а внутренней – функции находящиеся в скобках в степени.
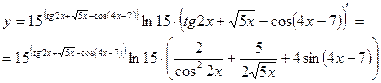
Задание 2.
В питательную среду вносят 10 кроликов. Рост числа кроликов описывается уравнением 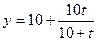 . Найти скорость роста числа кроликов в момент времени
. Найти скорость роста числа кроликов в момент времени 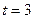 часа.
часа.
Решение.
Т. к. производная определяет скорость течения какого-либо процесса, то найдем 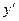 .
.
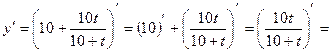
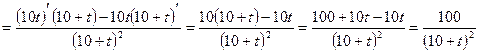
Скорость роста числа кроликов в момент времени 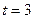 часа найдем, подставив в производную
часа найдем, подставив в производную 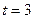 часа
часа
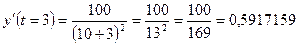 часа.
часа.
Задание 3
Найти угол наклона касательной к графику функции 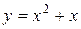 в точке
в точке 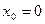 .
.
Решение.
Для нахождения угла наклона касательной к графику функции воспользуемся формулой
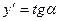 .
.
Получаем 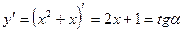 . Найдем значение производной в точке
. Найдем значение производной в точке 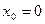 .
.
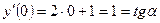
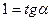
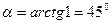 .
.
Т. об., угол наклона касательной к графику функции 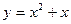 в точке
в точке 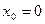 составляет
составляет 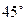 .
.
Задание 4
Вычислить приближенное значение 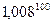 ,
, 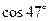 ,
, 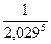 ,
, 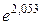 .
.
Решение.
а) Для вычисления приближенного значения 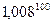 воспользуемся формулой
воспользуемся формулой
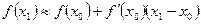 .
.
Введем обозначения: 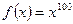 ,
, 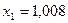 ,
, 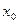 – это ближайшее целое число к числу
– это ближайшее целое число к числу 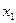 , поэтому
, поэтому 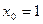 .
.
Далее вычисляем 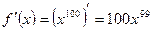 ,
, 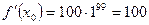 ,
, 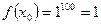 .
.
Т. об., получаем 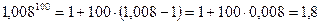 .
.
б) Для вычисления приближенного значения 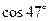 воспользуемся формулой
воспользуемся формулой
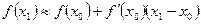 .
.
Введем обозначения: 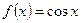 ,
, 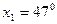 ,
, 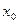 – это ближайшее табличное значение косинуса, поэтому
– это ближайшее табличное значение косинуса, поэтому 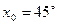 .
.
Далее вычисляем 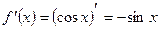 ,
, 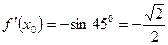 ,
, 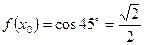 ,
, 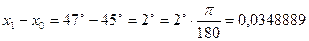 .
.
Т. об., получаем 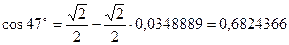 .
.
в) Для вычисления приближенного значения 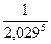 воспользуемся формулой
воспользуемся формулой
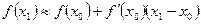 .
.
Введем обозначения: 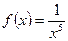 ,
, 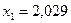 ,
, 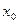 – это ближайшее целое число числу
– это ближайшее целое число числу 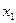 , поэтому
, поэтому 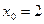 .
.
Далее вычисляем 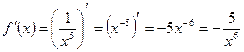 ,
, 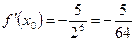 ,
, 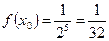 ,
, 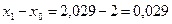 .
.
Т. об., получаем 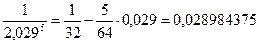 .
.
г) Для вычисления приближенного значения 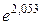 воспользуемся формулой
воспользуемся формулой
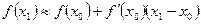 .
.
Введем обозначения: 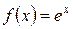 ,
, 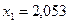 ,
, 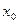 – это ближайшее целое число числу
– это ближайшее целое число числу 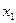 , поэтому
, поэтому 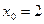 .
.
Далее вычисляем 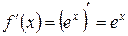 ,
, 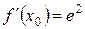 ,
, 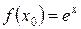 ,
, 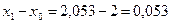 .
.
Т. об., получаем 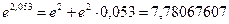 .
.
Задание 5
а) Найти интервалы возрастания и убывания функции, точки экстремума 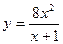 .
.
б) Найти наименьшее и наибольшее значение функции 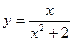 на отрезке
на отрезке 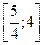
Решение.
а) Найти интервалы возрастания и убывания функции, точки экстремума 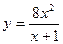 .
.
1. Найдем область определения функции 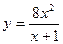 . Известно, что дробь определена, если ее знаменатель отличен от нуля. Поэтому получаем,
. Известно, что дробь определена, если ее знаменатель отличен от нуля. Поэтому получаем,
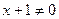
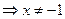 .
.
Т. об., получаем 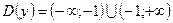 .
.
2. Вычисляем производную функции
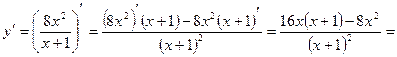
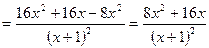
3. Решим уравнение 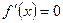 .
.
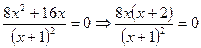
Дробь равна нулю тогда и только тогда, когда ее числитель равен нулю, а знаменатель отличен от нуля. Поэтому получаем систему вида
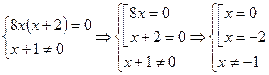 .
.
4. Рисуем числовую ось, расставляем числа в порядке возрастания и определяем знаки над промежутками.


5. Т. об., функция возрастает при 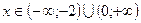 и функция убывает при
и функция убывает при 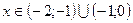 . Т. к. в точке
. Т. к. в точке 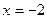 происходит смена знаков с «+» на «-», то данная точка является точкой максимума и т. к. в точке
происходит смена знаков с «+» на «-», то данная точка является точкой максимума и т. к. в точке 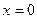 происходит смена знаков с «-» на «+», то данная точка является точкой минимума функции.
происходит смена знаков с «-» на «+», то данная точка является точкой минимума функции.
б) Найти наименьшее и наибольшее значение функции 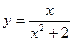 на отрезке
на отрезке 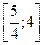 .
.
1. Найдем производную функции
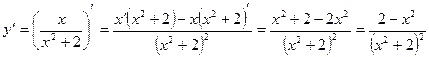
2. . Решим уравнение 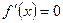 .
.
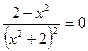
Дробь равна нулю тогда и только тогда, когда ее числитель равен нулю, а знаменатель отличен от нуля. Поэтому получаем систему вида
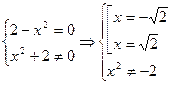 .
.
Значение 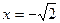 не принадлежит отрезку
не принадлежит отрезку 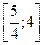 . Далее вычисляем значение функции в точке
. Далее вычисляем значение функции в точке 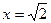 и на концах отрезка.
и на концах отрезка.
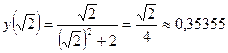 ;
; 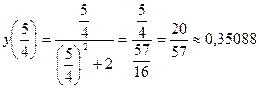 ;
;
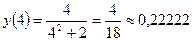 .
.
Т. об., 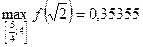 ,
, 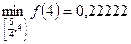 .
.
Приднестровский государственный университет
им. Т.Г. Шевченко
Физико-математический факультет
Кафедра «Алгебры, геометрии и методики преподавания математики»
Лабораторная работа №3
Вариант №___
Тема: «Применение производных к исследованию функций».
Выполнил(а) студент(ка)
медицинского факультета,
гр. ______
специальность «_________________»
Ф.И.О.
Проверил преподаватель
Ф.И.О.
| Дата сдачи | Дата возврата | Дата сдачи | Дата возврата | |
Тирасполь, 2017 г.
