Наибольшее и наименьшее значение функции
Наибольшим значением функции называется самое большее, наименьшим значением – самое меньшее из всех ее значений.
Функция может иметь только одно наибольшее и только одно наименьшее значение или может не иметь их совсем. Нахождение наибольшего и наименьшего значений непрерывных функций основывается на следующих свойствах этих функций:
1) Если в некотором интервале (конечном или бесконечном) функция y=f(x) непрерывна и имеет только один экстремум и если это максимум (минимум), то он будет наибольшим (наименьшим) значением функции в этом интервале.
2) Если функция f(x) непрерывна на некотором отрезке [a, b], то она обязательно имеет на этом отрезке наибольшее и наименьшее значения. Эти значения достигаются ее или в точках экстремума, лежащих внутри отрезка, или на границах этого отрезка.
Для отыскания наибольшего и наименьшего значений на отрезке рекомендуется пользоваться следующей схемой:
1. Найти производную 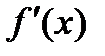 .
.
2. Найти критические точки функции, в которых 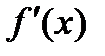 =0 или не существует.
=0 или не существует.
3. Найти значения функции в критических точках и на концах отрезка и выбрать из них наибольшее fнаиб и наименьшее fнаим.
При решении прикладных задач, в частности оптимизационных, важное значение имеют задачи на нахождение наибольшего и наименьшего значений (глобального максимума и глобального минимума) функции на промежутке Х. Для решения таких задач следует, исходя из условия, выбрать независимую переменную и выразить исследуемую величину через эту переменную. Затем найти искомое наибольшее или наименьшее значение полученной функции. При этом интервал изменения независимой переменной, который может быть конечным или бесконечным, также определяется из условия задачи.
Пример. Найти наибольшее и наименьшее значения функции 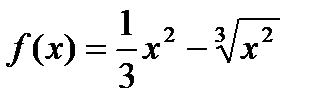 на промежутке
на промежутке 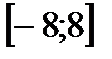 .
.
Решение: Заданная функция непрерывна на всей числовой оси. Производная функции
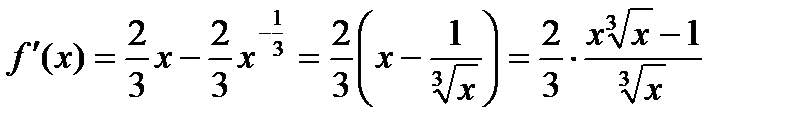 .
.
Производная 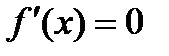 при
при 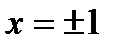 и
и 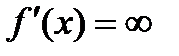 при
при 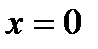 . Вычислим значения функции в этих точках:
. Вычислим значения функции в этих точках:
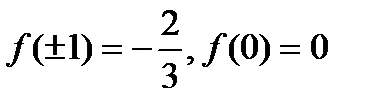 .
.
Значения функции на концах заданного промежутка равны 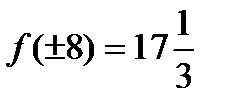 . Следовательно, наибольшее значение функции равно
. Следовательно, наибольшее значение функции равно 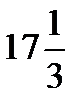 при
при 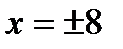 , наименьшее значение функции равно
, наименьшее значение функции равно 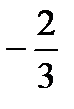 при
при 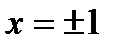 .
.
Раздел 2 Интегральное исчисление
Понятие неопределенного интеграла
Функция F(x)называется первообразной функции f(x) на интервале (а; b), если для любого
х ? (а; b) выполняется равенство
F’(x) = f(x) (или dF(x) = f(x) dx).
Множество всех первообразных функций F(x) + С для f(x) называется неопределенным интеграломот функции f(x) и обозначается символом 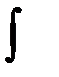 f(x)dx.
f(x)dx.
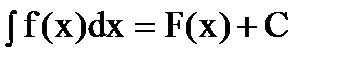 |
Здесь f(x) называется подынтегральной функцией,f(x)dx — подынтегральным выражением,х – переменной интегрирования, 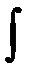 – знаком неопределенного интеграла.
– знаком неопределенного интеграла.
Операция нахождения неопределенного интеграла от функции называется интегрированием этой функции.
