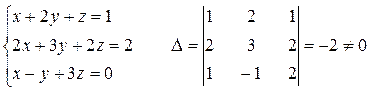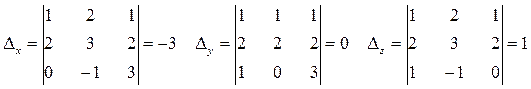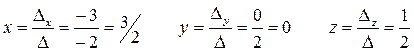Свойства операций над матрицами
1. 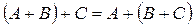 4.
4. 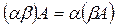
2. 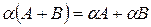 5.
5. 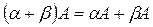
3. 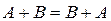 6.
6. 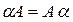
Возведение в степень
Можно возводить в степень только квадратные матрицы.
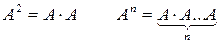
Пример: 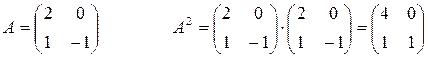
! Д/з: Рассмотреть все случаи, возникающие при умножении матрицы и привести примеры:
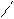 а)
а) 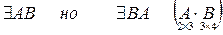
б) 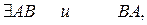 но разных размерностей
но разных размерностей 
в) ∃АВ и ВА одинаковых размерностей, АВ ≠ ВА
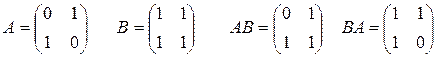
г) произведение двух ненулевых матриц может быть равно 0, т.е.
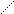
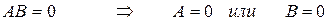
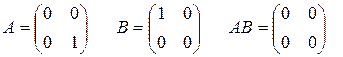
Транспонирование матриц
Если в матрице поменять местами строки и столбцы, получим транспонированную матрицу.
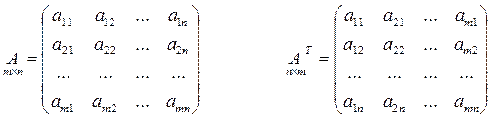
Пример: 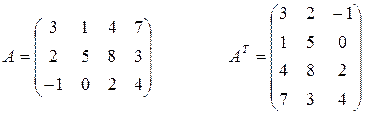
Свойства транспонирования:
1) 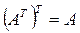
2) 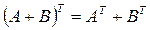
3) 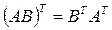
Определители и способы их вычисления
Каждая квадратная матрица имеет числовую характеристику, которая называется определителем матрицы.
Обозначение: матрица А определитель матрицы 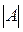
Если матрица А – первого порядка, то ее определителем является элемент а11
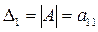
Если 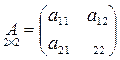 , то определителем матрицы А называется число
, то определителем матрицы А называется число
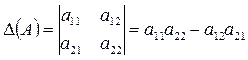
Пример:
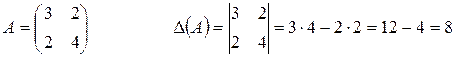
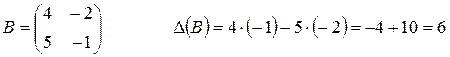
Определитель третьего порядка – число, получено по формуле:
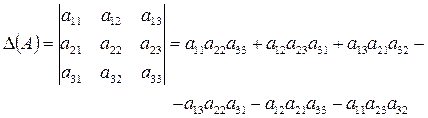
Для вычисления определителей 3-го порядка обычно пользуются 2-мя правилами:
1. Правило треугольника

















2. Правило Сарруса










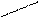
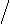
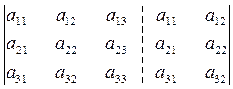
– – – + + +
Определитель 3-го порядка – это число, которое представляет собой алгебраическую сумму, состоящую из 6-ти слагаемых (т.е. 6-ти членов определителя). В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца.
Для вычисления определителей более высокого порядка необходимы дополнительные понятия.
Свойства определителей
1. Определитель не изменится при замене строк столбцами, т.е. транспонировании 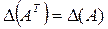
2. При перестановке двух строк (столбцов) матрицы ее определитель меняет знак на противоположный
3. Если все элементы строки (или столбца) матрицы умножить на число λ, то и определитель тоже умножится на λ.
4. Если квадратная матрица содержит две одинаковых строки или столбца, то ее определитель = 0.
Доказательство: Действительно, с одной стороны, если мы поменяем местами одинаковые строки (столбцы), то Δ не изменится, т.к. не изменится матрица, но по свойству (2) определитель меняет знак, т.е. Δ = –Δ ⇒ Δ = 0.
5. Если элементы двух строк или столбцов матрицы пропорциональны, то ее Δ = 0.
6. Если матрица содержит нулевую строку или столбец, то ее Δ = 0.
7. Определитель матрицы не изменяется, если к элементам какой-либо строки (столбца) матрицы прибавить элементы другой строки (столбца), уменьшенные на одно и то же число.
8.Если элементы какой-либо строки (столбца) определителя представляют собой сумму двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.
9. Определитель произведения матриц равен произведению определителей этих матриц:
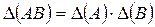
Общие понятия СЛУ
Опр.: Система m линейных уравнений с n неизвестными имеет вид:
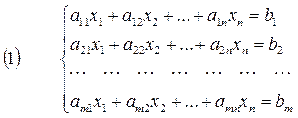
где aij, bi – произвольные числа;
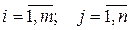 ;
;
aij – коэффициенты при неизвестных;
bi – свободные элементы;
i – номер уравнения;
j – номер неизвестного.
В матричном виде: 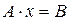 , где
, где
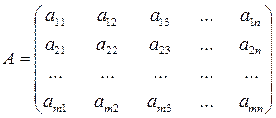 – матрица системы.
– матрица системы.
 – столбец неизвестных.
– столбец неизвестных. 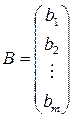 – столбец свободных элементов.
– столбец свободных элементов.
Опр.: Решением СЛУ (1) называется набор (массив) n чисел 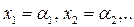
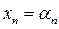 , при подстановке которых в эту систему каждое уравнение этой системы превращается в тождество.
, при подстановке которых в эту систему каждое уравнение этой системы превращается в тождество.
Опр.: СЛУ (1) называется совместной, если она имеет хотя бы одно решение; если система не имеет решений, она называется несовместной.
Совместная система имеет либо 1 решение и в таком случае она называется определенной, либо, если у нее больше 1 решения, она неопределенной.
Опр.: СЛУ вида (1) называется эквивалентными, если они имеют одно и то же множество решений.
Элементарные преобразования исходной системы приводит к эквивалентной системе.
Опр.: Матрица 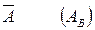
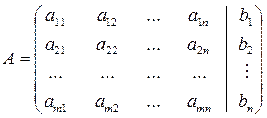
размерность m х (n+1) называется расширенной матрицей системы.
Теорема Кронекера-Канелли:
СЛУ совместна ⇔ когда ранг матрицы системы равен рангу расширенной матрицы системы.
Методы решения СЛУ
Матричный метод
Пусть m = n, тогда А – квадратная
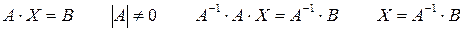
Пример:
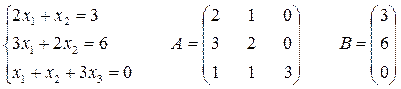
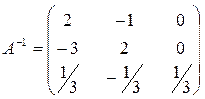 см. лекцию об обратной матрице.
см. лекцию об обратной матрице.
Тогда 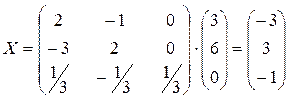
Ответ: 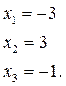
Метод Крамера
Опр.: Определитель 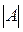 матрицы СЛУ называется определителем СЛУ и обозначается Δ.
матрицы СЛУ называется определителем СЛУ и обозначается Δ.
Заменим в этом определителе j-тый столбец на столбец свободных элементов В, получим другой определитель (обозначается Δj или Δxj).
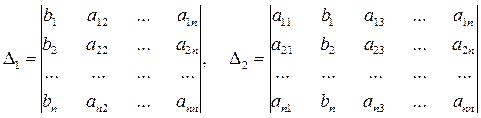 и т.д.
и т.д.
Теорема Крамера: Пусть Δ – определитель матрицы А СЛУ, Δj – определитель матрицы полученной из определителя Δ заменой j-того столбца на столбец B. Тогда, если Δ ≠ 0, то СЛУ имеет единственное решение:
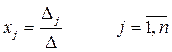
! Д/з: Доказательство самостоятельно (учебник Крамера, Красса).
Пример: