Имитационный виртуальный эксперимент.

Воспользуемся датчиком случайных чисел:

Теперь необходимо получить правую часть матрицы планирования, составленной на первом этапе исследования, содержащую значения функции отклика. Так как нам аналитически заданы математическое ожидание и дисперсия, то есть возможность получить два набора функции отклика. Затем сравнить их между собой и с искомой моделью. Пусть, сначала, функцией отклика будут значения математического ожидания, затем значения дисперсии. Полученные значения функций отклика выпишем в отдельную матрицу DE, в первый столбец по математическому ожиданию, во второй по дисперсии.

Проанализируем поверхность отклика для экспериментальной модели. Рассчитаем коэффициенты математической модели:

Зададим массивы изменения значений факторов от минимального к максимальному, с шагом 0,1 и определим количество шагов:

Рассчитаем массивы со значениями факторов:

Найдем значения функции отклика:

По экспериментальной модели:

По математическому ожиданию:

Получили матрицы размерности 40х30, именно на столько частей были разбиты диапазоны изменения значений факторов.

Сравним рассчитанные поверхности на графике:

Рисунок 8 – Экспериментальная и теоретическая (по мат. ожиданию) поверхности

Визуально характеризовать, адекватность полученной модели сложно. Получим характеристики, численно характеризующие схожесть полученных моделей.

Рассчитаем коэффициент корреляции, характеризующий тесноту связи экспериментальной и теоретической моделей.

Рассчитаем значение функции отклика по дисперсии:

На рисунке 2 представлена найденная поверхность в сравнении с экспериментальной.

Рисунок 9 – Экспериментальная и теоретическая (по дисперсии) поверхности

Рассчитаем численные характеристики, как для предыдущего случая:

Коэффициент корреляции:

Вывод

В ходе планирования эксперимента были построены математические модели: экспериментальная и теоретическая (по математическому ожиданию и по дисперсии). По моделям были получены функции отклика, которые мы сравнили с экспериментальной функцией отклика (графически и численно). По рассчитанным коэффициентам корреляции видно, что функция отклика, построенная по математическому ожиданию, является точнее, т.е. воспроизводит результаты эксперимента лучше, ближе к реальному эксперименту. Следовательно, ее можно взять за основу проведения виртуального эксперимента.

Лабораторная работа 3. Рассмотрение методики диагностики оборудования на примере электроприводной арматур

Теоретическая часть.

Диагностические параметры сигналов активной мощности и токовых сигналов ЭПА

Анализ неисправностей электрических машин, опыт эксплуатации ЭПА показывает, что для определения вида технического состояния (оценки работоспособности) электроприводной арматуры, находящейся в составе технологических систем энергоблоков ТЭС и АЭС, достаточно информативным является токовый сигнал (сигнал активной мощности) электродвигателя, рассчитанный для одной и/или трех фаз.

В результате анализа кинематических схем приводов и данных измерений сигналов тока и активной мощности была принята за эталон циклограмма сигналов активной мощности «открытие-закрытие» идеальной модели ЭПА, где координаты точек и геометрические параметры отрезков циклограмм используются для расчета диагностических параметров технического состояния арматуры.

Циклограммы содержат необходимые признаки, характеризующие динамику перемещения и кинематические особенности передаточных звеньев исполнительных механизмов арматуры, электропривода и электродвигателя.

На рисунках 10 и 11 приведена типичная форма токового сигнала (сигнала активной мощности), регистрируемого при выполнении операции «Открытие» и «Закрытие» при отсутствии расхода рабочей среды. Под формой токового сигнала понимается огибающая переменной составляющей исходного токового сигнала. Приведенная форма сигналов характерна для задвижек. Для регулирующих клапанов и вентилей форма сигнала может отличаться от формы, приведенной на рисунках 3 и 4 (например, отсутствием тока срыва и уплотнения).

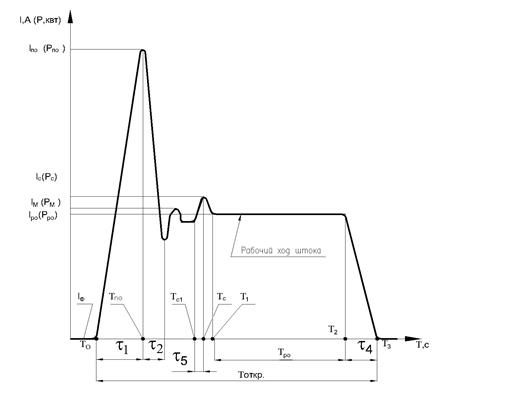
Рисунок 10 – Циклограмма токового сигнала (сигнала активной мощности) при выполнении операции «Открытие»

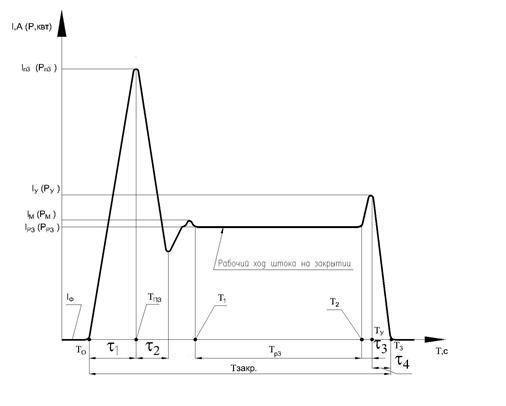
Рисунок 11 – Циклограмма токового сигнала (сигнала активной мощности) при выполнении операции «Закрытие»