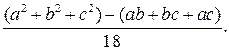Основные статистические распределения

Нормальное распределение

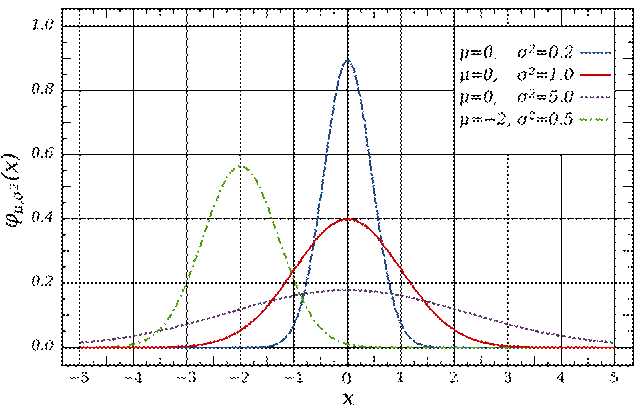
Нормальное распределение (рис. 2) является теоретической моделью случайной величины, представляющей собой сумму константы с бесконечно большим количеством независимых случайных величин (помех), распределённых по произвольным законам на интервале (–¥; ¥). Данная константа равна математическому ожиданию нормально распределённой случайной величины.

Функция плотности вероятности нормального распределения:

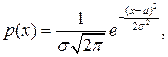
где x — значение случайной величины, m — её математическое ожидание, s — среднее квадратическое отклонение, e » 2,7182818 — основание натурального логарифма.

Функция нормального распределения не выражается через элементарные функции и вычисляется с использованием численных методов интегрирования (например, метода трапеций). Математическая запись:

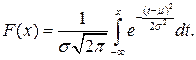
В Excel плотность распределения вероятности нормального распределения для значения, хранящегося в ячейке Значение, вычисляется с помощью формулы

=НОРМРАСП(Значение;Средняя;Корень(Дисперсия);0),

где Средняя и Дисперсия — имена ячеек, содержащих соответствующие значения. Значение функции нормального распределения (вероятности того, что нормально распределённое случайное значение не превысит указанную величину) вычисляется с помощью формулы

=НОРМРАСП(Значение;Средняя;Корень(Дисперсия);1).

Определить величину, которую с заданной вероятностью не превысит нормально распределённое случайное значение, можно с помощью формулы

=НОРМОБР(Вероятность;Средняя;Корень(Дисперсия)),

где Вероятность — имя ячейки, содержащей требуемое значение вероятности.

Источник: http://ru.wikipedia.org

Рис. 2. Графики нормального распределения.

Равномерное распределение

Равномерное распределение (рис. 3) не характерно для случайных величин, описывающих экономические, социальные и природные процессы[11]. Однако оно может оказаться подходящим приближением к реальному (неизвестному) распределению при следующих условиях:

¨ диапазон вариации случайной величины x заключён между значениями a и b, каждое из которых имеет интерпретацию в терминах исследуемого процесса (подобно тому, как температура воды при атмосферном давлении может быть распределена между 0 и 100°C);

¨ среднее и модальное значения отличаются от медианы (a+b)/2 несущественно;

¨ дисперсия исследуемой случайной величины отличается от величины (b–a)2/12 несущественно;

¨ на гистограмме эмпирического распределения отсутствуют выраженные вершины.

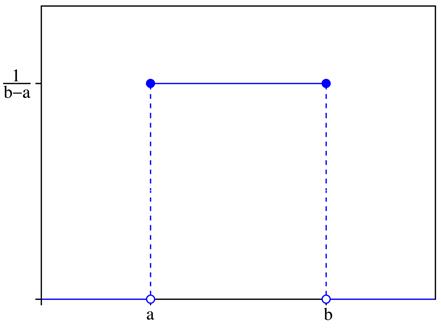
Источник: http://ru.wikipedia.org

Рис. 3. График равномерного распределения.

Обычно равномерное распределение оказывается приемлемой моделью только при малом числе наблюдений случайной величины. Принятие гипотезы о равномерном распределении, как правило, означает недостаточную степень изученности моделируемой случайной величины, но может оказаться лучшей гипотезой из всех, которые не могут быть отвергнуты на имеющихся опытных данных.

Функция плотности вероятности равномерного распределения:

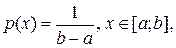
где x — значение случайной величины, a и b — границы множества её значений.

Функция равномерного распределения:

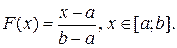
Математическое ожидание равномерно распределённой случайной величины равно (a+b)/2; дисперсия — (b–a)2/12.

Треугольное распределение

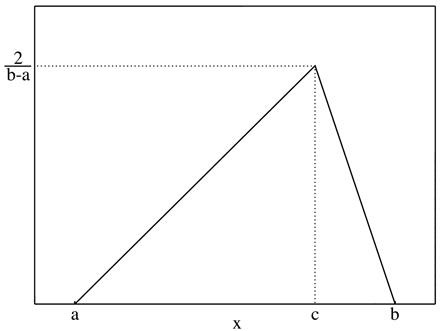
Треугольное распределение (рис. 4) не характерно для случайных величин, описывающих экономические, социальные и природные процессы[12]. Однако оно может оказаться подходящим приближением к реальному распределению при следующих условиях:

¨ диапазон вариации случайной величины x заключён между значениями a и b, каждое из которых имеет интерпретацию в терминах исследуемого процесса (подобно тому, как температура воды при атмосферном давлении может быть распределена между 0 и 100°C);

¨ есть основания считать, что при x ® a и при x ® b плотность вероятности стремится к нулю;

¨ известно модальное значение случайной величины, равное c;

¨ среднее значение отличается от величины (а+b+c)/3 несущественно;

¨ дисперсия исследуемой случайной величины отличается от величины

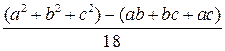
несущественно.

Обычно треугольное распределение оказывается приемлемой моделью только при малом числе наблюдений случайной величины. Принятие гипотезы о треугольном распределении, как правило, означает недостаточную степень изученности моделируемой случайной величины, но может оказаться лучшей гипотезой из всех, которые не могут быть отвергнуты на имеющихся опытных данных.

Источник: http://en.wikipedia.org

Рис. 4. График треугольного распределения.

Функция плотности вероятности равномерного распределения:

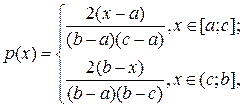
где x — значение случайной величиныˆ, a и b — границы множества её значений, c — модальное (наиболее часто встречающееся) значение.

Функция треугольного распределения:

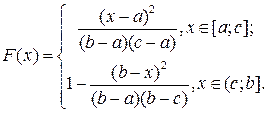
Математическое ожидание случайной величины, распределённой по треугольному закону, равно (a+b+с)/3; дисперсия составляет