Линейные, билинейные и квадратичные функции в линейном пространстве.
8.1. Линейная функция в линейном пространстве и ее представление в заданном базисе.
8.2. Билинейная функция в линейном пространстве и соответствующая ей билинейная форма в заданном базисе. Векторно-матричная запись билинейной формы. Матрица билинейной формы, закон ее изменения при переходе к новому базису и инвариантность ранга этой матрицы.
8.3. Квадратичная функция в линейном пространстве. Симметричные билинейные функции и соответствующие им квадратичные функции. Квадратичные функции и соответствующие им квадратичные формы. Матрица квадратичной формы и закон ее изменения при переходе к новому базису.
Приведение квадратичной формы к каноническому и нормальному виду.
9.1. Канонический и нормальный вид квадратичной формы.
9.2. Метод Лагранжа приведения квадратичной формы к каноническому и нормальному виду.
9.3. Положительный и отрицательный индексы, ранг квадратичной формы. Закон инерции. Три инварианта квадратичной формы.
Знакопеременные, знакопостоянные и знакоопределенные квадратичные формы.
10.1. Знакопеременные, знакопостоянные квадратичные формы (определения, примеры). Их канонический и нормальный вид, индексы и ранг.
10.2. Знакоопределенные (положительно и отрицательно определенные) квадратичные формы. Их канонический и нормальный вид. Индексы и ранг знакоопределенной формы.
10.3. Критерий Сильвестра положительной (отрицательной) определенности квадратичной формы.
Евклидово пространство.
11.1. Определение евклидова пространства. Евклидово скалярное произведение. Примеры евклидовых пространств.
11.2. Неравенство Коши-Буняковского.
11.3. Длина вектора и угол между векторами в евклидовом пространстве.
11.4. Неравенство треугольника.
Матрица Грама.
12.1. Координатная и векторно-матричная запись скалярного произведения в заданном базисе. Матрица Грама и ее свойства. Примеры матриц Грама.
12.2. Преобразование матрицы Грама при переходе к новому базису.
12.3. Нахождение матрицы Грама скалярного произведения в базисе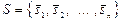 
пространства 
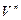геометрических векторов в случае, когда скалярное произведение в каноническом (ортонормированном) базисе 
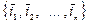этого пространства задается стандартным образом.
Ортонормированный базис.
13.1. Ортогональная система векторов, ее линейная независимость.
13.2. Ортогональный и ортонормированный базисы. Матрица Грама, запись скалярного произведения векторов и длин векторов в этих базисах. Теорема Пифагора в произвольном и ортонормированном базисах евклидова пространства.
13.3. Метод ортогонализации базиса.
Ортогональные операторы в евклидовом пространстве.
14.1. Ортогональные матрицы и их свойства.
14.2. Ортогональный оператор и его свойства.
14.3. Связь ортогональных операторов с ортогональными матрицами.