Математические модели на микроуровне
Математическими моделями на микроуровне являются дифференциальные уравне- ния в частных производных или интегральные уравнения, описывающие поля физических величин. Другими словами, на микроуровне используются модели с распределенными па- раметрами. В качестве независимых переменных в моделях могут фигурировать про- странственные переменные и время.
Характерными примерами моделей могут служить уравнения математической физи- ки вместе с заданными краевыми условиями.
В САПР решение дифференциальных или интегро-дифференциальных уравнений с частными производными выполняется численными методами. Эти методы основаны на дискретизации независимых переменных — их представлении конечным множеством значений в выбранных узловых точках исследуемого пространства. Эти точки рассматри- ваются как узлы некоторой сетки, поэтому используемые в САПР методы — это сеточ- ные методы.
Среди сеточных методов наибольшее распространение получили два метода: метод конечных разностей (МКР) и МКЭ [2, 4, 9]. Обычно выполняют дискретизацию простран- ственных независимых переменных, т. е. используют пространственную сетку. В этом случае результатом дискретизации является СОДУ для задачи нестационарной или систе- ма алгебраических уравнений для стационарной.
Поскольку МКЭ представляет собой один из методов дискретизации, то число сте- пеней свободы конечно-элементной модели необходимо конечно. Обычно, все степени свободы собираются в матричный вектор, обозначаемый Uи называемый вектором сте- пеней свободы или вектором состояния. Термин вектор узловых перемещений обычно используется в механических приложениях.
В аналитической механике каждой степени свободы соответствует сопряженная пере- менная, представляющая собой обобщенную силу. В немеханических приложениях также существует подобное множество сопряженных переменных, которые для универсальности называются силами или силовыми переменными. Эти силы объединяются в матричный
вектор, обозначаемый F. Отметим, что внутреннее произведение вектора сил на вектор степеней свободы имеет смысл внешней энергии или работы.
Предполагается, что соотношение между Uи Fявляется линейным и однородным. Последнее означает, что если Uстремится к нулю, то и Fстремится к нулю, в этом случае соотношение между ними выражается следующим основным уравнением:
KU=F
Kдля универсальности называется матрицей жесткости, даже в случае нечисто ме- ханических приложений, поскольку к настоящему времени нет общего соглашения по обозначению этой матрицы в различных дисциплинах.
Физический смысл векторов Uи Fизменяется в зависимости от области приложения МКЭ, как это показано в таблице 1.1.
Таблица 1.1. Физический смысл векторов U и F в различных приложениях
| Область приложения | Вектор состояния U | Сопряженный вектор F |
| Механика твердых тел | Перемещение | Механическая сила |
| Теплопроводность | Теплопроводность | Тепловой поток |
| Механика жидкости и газа | Скорость | Поток |
| Электростатика | Электрический потенциал | Плотность заряда |
| Магнитостатика | Магнитный потенциал | Интенсивность магнитного поля |
Основные шаги МКЭ
Основные шаги МКЭ показаны на рис. 1.2. Схематично их можно назвать следующим образом:
· Идеализация
· Дискретизация
· Решение.
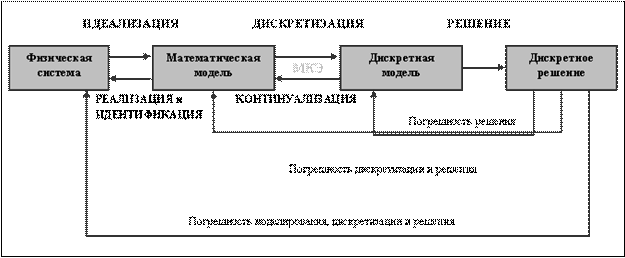
Рис.1.2. Основные шаги МКЭ
Идеализация. Под идеализацией понимают процесс перехода от исходной физиче- ской системы к математической модели. Этот процесс является наиболее важным шагом при решении технической или инженерной задачи.
Ключевым пунктом в этом процессе является понятие модели, которую можно опре- делить как символическое устройство, построенное для моделирования и предсказания поведения системы. Математическое моделирование, или идеализация, есть процесс, с помощью которого инженер переходит от реальной физической системы к математиче- ской модели системы. Данный процесс называется идеализацией, поскольку математиче- ская модель необходимо абстрагируется от физической реальности.
В качестве примера реальной физической системы рассмотрим инженерную конст- рукцию в виде плоской пластины, нагруженную поперечными силами. Математические модели данной системы, которые инженер может использовать для анализа напряжений в пластине, могут быть следующими [7, 17]:
1. Модель очень тонкой пластины, основанная на теории изгиба мембран.
2. Модель тонкой пластины, основанная на классической теории Кирхгоффа.
3. Модель достаточно толстой пластины, основанная, например, на теории Миндлина-Рейсснера.
4. Модель очень толстой пластины, основанная на трехмерной теории упруго-
сти.
Очевидно, инженер должен обладать достаточными теоретическими знаниями, чтобы правильно выбрать соответствующую математическую модель системы (конструкции), которую ему необходимо исследовать.
Дискретизация области, т.е. замена континуальной среды совокупностью КЭ задан- ной формы, соединенных между собой в узлах конечным числом связей.
Этот этап, несмотря на видимую простоту, имеет важное значение, хотя он и не обу- словлен строгими теоретическими рекомендациями и во многом определяется интуитив- но. Обычно при построении конечно-элементной модели руководствуются предваритель- ными представлениями о характере ожидаемого результата, и в местах высоких градиен- тов искомых величин сетку конечных элементов сгущают.
Решение
