Математические модели элементарных

Измерительных сигналов

К элементарным измерительным сигналам относятся постоянный во времени сигнал и сигналы, описываемые единичной и синусоидальной функциями, а также дельта-функцией.

Постоянный сигнал — самый простой из элементарных сигналов, описываемый математической моделью вида Y = А, где А — единственный параметр сигнала. Графики временной и частотной моделей постоянного сигнала приведены на рис. 10.4.

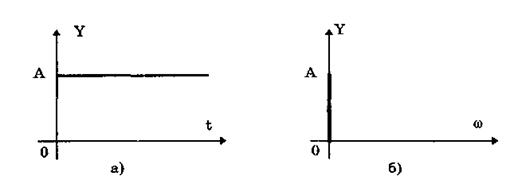
Рис. 10.4. Графики временной (а) и частотной (б) моделей

постоянного сигнала

Единичная функция, называемая иногда функцией Хевисайда, описывается уравнением

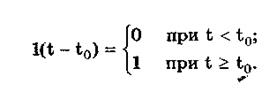
Она имеет один параметр — момент времени t₀. Ее временная и частотная модели представлены на рис. 10.5,а.

Дельта-функция описывается уравнением

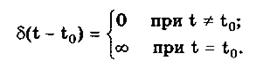
Она также имеет один параметр — момент времени t₀. Графики временной и частотной моделей дельта-функции d(t) показаны на рис. 10.5, б. Из них видно, что дельта-функция имеет спектр бесконечной ширины.

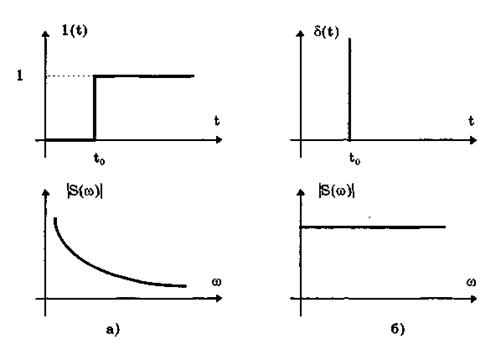
Рис. 10.5. График моделей единичной (а) и дельта-функции(б)

Дельта-функция обладает следующим свойством:

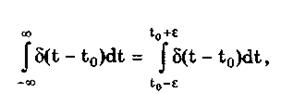
где e — любое, сколь угодно малое число. Она может рассматриваться как предельная функция однопараметрического семейства непрерывных функций, например нормального распределения с бесконечно малым СКО s:

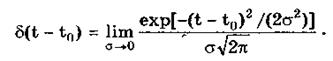
Единичная и дельта-функции связаны между собой следующими выражениями:

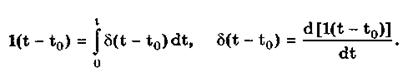
Важной особенностью дельта-функции является стробирующее действие, которое описывается уравнением

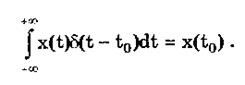
Оно используется для представления дискретизированной во времени функции с шагом дискретизации Dt:

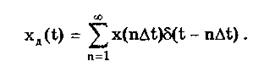
Гармонический сигнал описывается уравнением

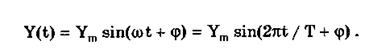(10.5)

Параметрами такого сигнала являются: амплитуда Y_m, период Т (или частота f=l/T, или круговая частота w) и начальная фаза j. График временной модели общеизвестен, а график частотной модели такого сигнала показан на рис. 10.6

.

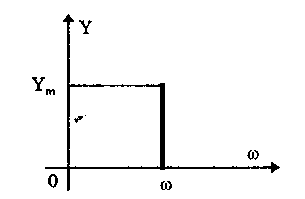
Рис. 10.6. Спектр гармонического сигнала

Математические модели сложных

Измерительных сигналов

В средствах измерений используется большое число измерительных сигналов, имеющих самые разнообразные формы. Рассмотрим некоторые из них, наиболее часто встречающиеся на практике.

Прямоугольные импульсы. Одиночный идеальный прямоугольный импульс (рис. 10.7,а) описывается уравнением

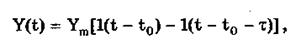
т.е. он формируется как разность двух единичных функций, сдвинутых во времени на величину т — длительность импульса.

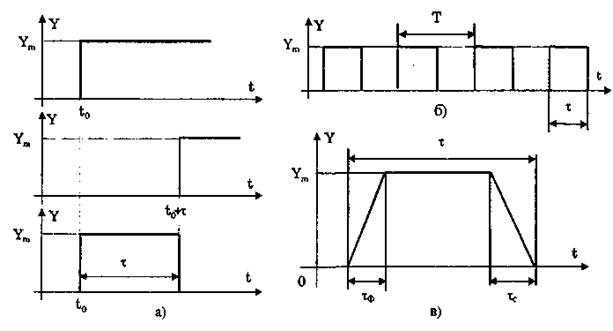
Рис. 10.7. Формирование идеального прямоугольного импульса (а),

последовательность прямоугольных импульсов (б) и

трапецеидальный импульс (в)

Последовательность прямоугольных импульсов есть сумма одиночных импульсов:

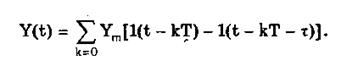
Для ее описания необходимо знать три параметра: амплитуду Y_m, длительность Т и период Т (рис. 10.7, б). Отношение периода к длительности прямоугольного импульса называется скважностью, а обратная величина — коэффициентом заполнения. При скважности, равной двум, последовательность импульсов называют меандром (см. рис. 10.7, б).

Идеальные прямоугольные импульсы в природе не встречаются. В реальных импульсах время изменения сигнала от нулевых до амплитудных значений (и обратно) всегда имеет конечную длительность, т.е. фронт Т_ф и спад Т_с (рис. 10.7, в). Следовательно, у реальных импульсов будет трапецеидальная форма.

Трапецеидальный импульс также является идеализации реальных импульсов, которые имеют гораздо более сложную форму. Она отличается от трапеции спадом вершины импульса, выбросами на вершине и в паузе и другими особенностями, учтенными в системе параметров реального прямоугольного импульса по ГОСТ 16465-70.

Сигналы с линейными участками. При построении средств измерительной техники широкое применение находят периодические сигналы с линейными участками. Это прежде всего линейный знакопеременный и однополярный линейно изменяющийся (пилообразный) сигналы (рис. 10.8). Линейный знакопеременный сигнал описывается уравнением

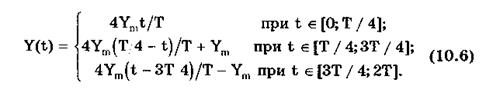
Пилообразный сигнал

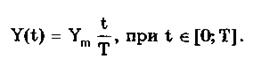
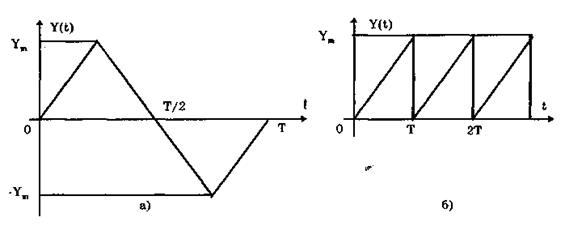
Рис. 10.8. Линейный знакопеременный (а) и однополярный

линейно изменяющийся (пилообразный) (б) сигналы

Пример 10.1. Оценить нижнюю и верхнюю частоты полосы пропускания измерительного канала средства измерений, используемого для определения параметров трех сигналов одинаковой частоты <й и амплитуды Y_m=A:

Yj(t) — синусоидального, описываемого формулой (10.5) при j = 0;

Y₂(t) — линейного знакопеременного, описываемого формулой (10.6);

Y₃(t) — знакопеременного меандра, описываемого формулой

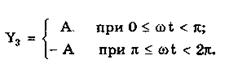
Чтобы средство измерений позволяло точно определять параметры сигнала, оно не должно искажать его форму в процессе преобразований. Для этого все гармоники сигнала должны проходить через измерительный канал без искажений. Выполнение данного условия нереально, так как полоса пропускания СИ конечна, а число гармоник в спектре бесконечно. Поэтому в качестве критерия выбора максимальной частоты полосы пропускания измерительного канала примем следующее условие: для внесения минимальных искажений в форму измеряемого сигнала канал должен пропускать без искажений его гармоники, амплитуда которых превышает, например, 1% амплитуды первой гармоники. Это не очень строгая постановка вопроса, однако она позволит решить поставленную задачу.

Определим спектральный состав измеряемых сигналов, разложив их в ряд Фурье:

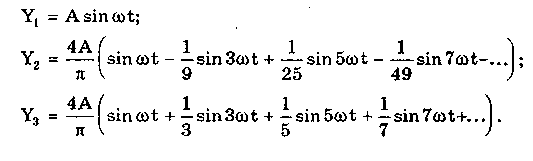
Спектр первого сигнала содержит только первую гармонику с амплитудой А. Спектры второго и третьего сигналов содержат только нечетные гармоники, амплитуда которых затухает с разной интенсивностью: у сигнала Y₂ — пропорционально 1/n², где n — номер гармоники, а у сигнала Y₂ — пропорционально 1/n. Соответственно номер гармоники второго сигнала, после которой их амплитуда становится меньше 0,01A₁, равен 11 (100/11²=0,83%). Для третьего сигнала это номер 101 (100/101=0,99%).

Таким образом, при измерении синусоидального сигнала минимальная и максимальная частоты полосы пропускания канала одинаковы и равны со. При измерении линейного знакопеременного сигнала они соответственно составят w и 11w. Полоса пропускания равна 10w. Для знакопеременного меандра экстремальные частоты равны w и 101w, а полоса пропускания — 100w.

Модулированные сигналы. Модулированным называется сигнал, являющийся результатом взаимодействия двух или более сигналов, т.е. модуляции. Модуляция — это воздействие измерительного сигнала X(t) на какой-либо параметр стационарного сигнала Y(t), обладающего такими физической природой и характером изменения во времени, при которых удобны его дальнейшие преобразования и передача. В качестве стационарного сигнала, именуемого несущим, обычно выбирают синусоидальное (гармоническое) колебание

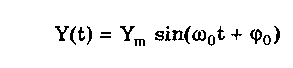(10.7)

или последовательность импульсов.

Физический процесс, обратный модуляции, называется демодуляцией, или детектированием, и заключается в получении из модулированного сигнала другого сигнала, пропорционального модулирующему. Задача демодуляции — по возможности полное восстановление информации, содержащейся в модулирующем сигнале X(t).

Вид модуляции и способ детектирования зависят от требований, предъявляемых к точности передачи информации. Наиболее простым модулированным гармоническим сигналом является ам-плитудно-модулированный сигнал, в котором измерительная информация содержится в амплитуде несущего синусоидального сигнала (рис. 10.9).

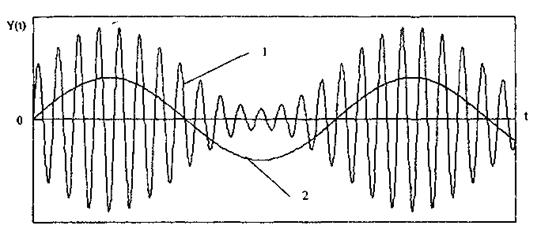
Рис. 10.9. Амплитудно-модулированный (1) и

модулирующий (2) сигналы

Амплитудно-модулированные сигналы описываются формулой

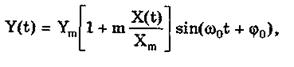(10.8)

где m — глубина амплитудной модуляции (всегда меньше единицы). При частотной модуляции (рис. 10.10) измерительная информация содержится в частоте модулированного сигнала, т.е.

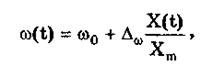
где D_w — наибольшее изменение частоты модулированного сигнала, т.е. девиация частоты, пропорциональная амплитуде модулирующего сигнала.

При фазовой модуляции (рис. 10.11) модулирующий сигнал X(t) воздействует на фазу несущего колебания:

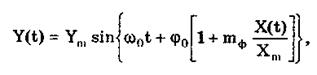
где m_ф — коэффициент фазовой модуляции.

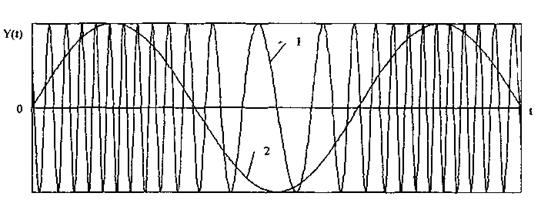
Рис. 10.10. Частотно-модулированный (1) и модулирующий (2) сигналы

Для того чтобы при детектировании можно было восстановить модулирующий сигнал, необходимо иметь сигнал вида (10.7), называемый опорным. Относительно него наблюдают, как меняется фаза модулированного сигнала. Модулирующий, модулированный и опорный сигналы показаны на рис. 10.11.

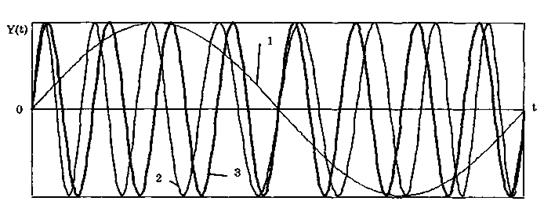
Рис. 10.11. Модулирующий (1), фазомодулированный (2) и

опорный (3) сигналы

Если модулируемым сигналом является периодическая последовательность прямоугольных импульсов, уо возможны три вида модуляции (рис. 10.12):

• амплитудно-импульсная (АИМ);

• частотно-импульсная (ЧИМ);

• широтно-импульсная (ШИМ).

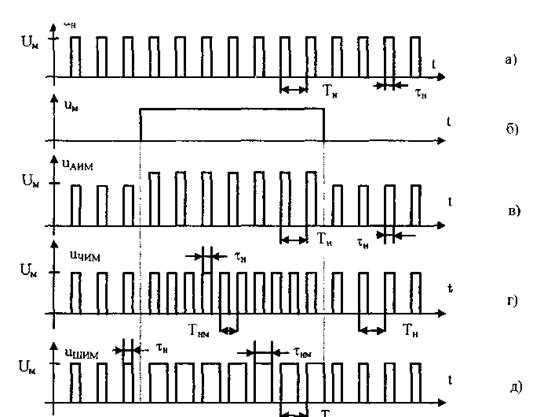
Рис. 10.12. Несущая последовательность прямоугольных импульсов (а), модулирующий (б), амплитудно-модулированный (в), частотно-модулированный (г) и широтно-модулированный (д) сигналы

При этом параметром, несущим измерительную информацию, соответственно являются амплитуда, частота и длительность импульсов.