Численное решение обыкновенных дифференциальных

Уравнений

Многие задачи физики, химии, экологии, механики и других разделов науки и техники при их математическом моделировании сводятся к дифференциальным уравнениям. Поэтому решение дифференциальных уравнений является одной из важнейших математических задач. В вычислительной математике изучаются численные методы решения дифференциальных уравнений, которые особенно эффективны в сочетании с использованием персональных компьютеров.

Среди множества численных методов решения дифференциальных уравнений наиболее простые – это явные одношаговые методы. К ним относятся различные модификации метода Рунге-Кутта.

Постановка задачи:

Требуется найти функцию у = у(х), удовлетворяющую уравнению

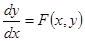(2.3)

и принимающую при х = х₀ заданное значение у₀:

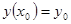. (2.4)

При этом решение необходимо получить в интервале х₀ £ х £ х_к. Из теории дифференциальных уравнений известно, что решение у(х) задачи Коши (2.3), (2.4) существует, единственно и является гладкой функцией, если правая часть F(x, y) удовлетворяет некоторым условиям гладкости. Численное решение задачи Коши методом Рунге-Кутта 4-го порядка заключается в следующем. На заданном интервале [х₀, х_к] выбираются узловые точки. Значение решения в нулевой точке известно у(х₀) = у₀. В следующей точке у(х₁) определяется по формуле

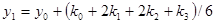, (2.5)

здесь

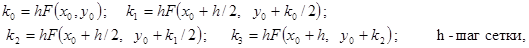(2.6)

т. е. данный вариант метода Рунге-Кутта требует на каждом шаге четырехкратного вычисления правой части уравнения (2.3). Этот алгоритм реализован в программе ode45.Кроме этой программы MATLAB располагает обширным набором аналогичных программ, позволяющих успешно решать обыкновенные дифференциальные уравнения.

Пример 5. Решить задачу Коши

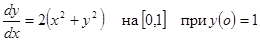. (2.7)

Точное решение имеет вид

.

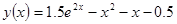Выполним решение данной задачи с помощью программы ode45. Вначале в М-файл записываем правую часть уравнения (2.7), сам М-файл оформляется как файл – функция, даем ему имя F:

function dydx = F(x, y)

dydx = zeros(1,1);

dydx(1) = 2*(x^2+y(1));

Для численного решения задачи Коши в окне команд набираются следующие операторы.

Протокол программы.

>>[X Y] = ode45 ( @ F , [0 1] , [1] ) ;

% Дескриптор @ обеспечивает связь с файлом – функцией правой части

% [0 1] – интервал на котором необходимо получить решение

% [1] – начальное значение решения

>> рlot (X,Y) ;

>> % Построение графика численного решения задачи Коши (2.7)

>> hold on; gtext ( ¢ y(x) ¢)

% Команда позволяет с помощью мышки нанести на график надпись у(х)

>> [X Y]

>> % Последняя команда выводит таблицу численного решения задачи.

Результаты решения. График решения задачи Коши (2.7) показан на рис. 2.3. Численное решение представлено в таблице 2.4, где приведены только отдельные узловые точки. В программе ode45по умолчанию интервал разбивается на 40 точек с шагом h = 1/40 = 0.025.

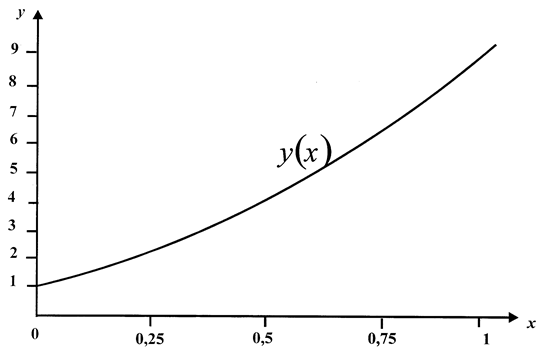Рис. 2.3

Таблица 2.4

хi	Метод Рунге-Кутта	Точное решение
0.0	1.0	1.0
0.1	1.2221	1.2221
0.2	1.4977	1.4977
0.3	1.8432	1.8432
0.4	2.2783	2.2783
0.5	2.8274	2.8274
0.6	3.5202	3.5202
0.7	4.3928	4.3928
0.8	5.4895	5.4895
0.9	6.8645	6.8645
1.0	8.5836	8.5836

Как следует из таблицы 2.4 численное решение программой ode45является точным.

Варианты заданий. Построить график и вывести в виде таблицы решение задачи Коши на интервале [0; 1] методом Рунге-Кутта 4-го порядка. Данные взять из таблицы 2.5.

Таблица 2.5

№ п/п	f(x,y)	y0
1.		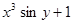0.0
2.		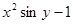0.1
3.		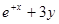2.0
4.		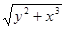0.3
5.		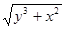0.4
6.		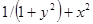0.0
7.		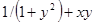0.1
8.		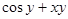0.2
9.		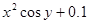0.3
10.		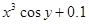0.4
11.		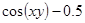0.5
12.		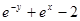0.0
13.		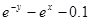0.5
14.		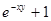0.4
15.		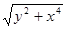0.3
16.		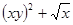0.2
17.		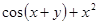0.1
18.		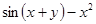0.0
19.		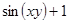0.1
20.		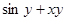0.2
21.		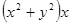0.3
22.		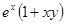0.4
23.		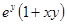0.5
24.		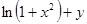0.6
25.		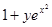0.7
26.		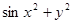0.0
27.		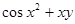0.1
28.		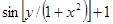0.2
29.		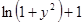0.3
30.		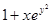0.4