Телеграфные уравнения. Решение телеграфных уравнений для случая установившегося гармонического режима

Для описания изменений тока и напряжения вдоль длинной линии составим уравнения электрического равновесия для бесконечно малого участка длинной линии (рис. 1) по законам Кирхгофа с использованием компонентных соотношений для сосредоточенных элементов. Будем при этом полагать, что длинная линия является однородной.

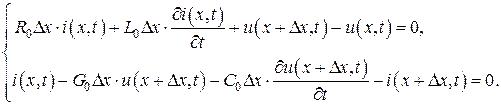(1)

Перегруппируем уравнения системы (1) в следующем виде:

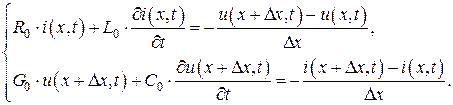(2)

Правые части уравнений системы (2) при предельном переходе 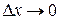есть ни что иное как производные напряжения и тока по пространственной координате, взятые со знаком минус:

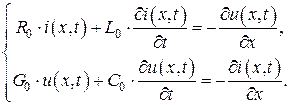(3)

Система уравнений (3) носит название телеграфных уравнений, поскольку впервые была получена именно для этого вида цепей с распределенными параметрами.

В дальнейшем будем рассматривать установившийся гармонический режим вдоль всей длинной линии. Это обусловлено тем, что большинство радиотехнических устройств преимущественно работает с гармоническими сигналами. С этой целью перейдем от мгновенных значений токов и напряжений к их комплексным мгновенным значениям вида:

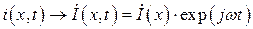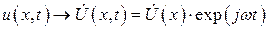, . (4)

Тогда производные по времени могут быть легко вычислены:

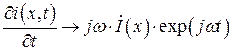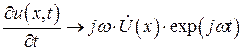, , (5)

и после подстановки замен (4), (5) в систему телеграфных уравнений (3) и сокращения всех членов уравнений системы на общий множитель 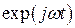она принимает вид:

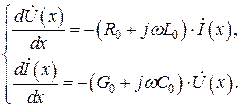(6)

Эта система связанных дифференциальных уравнений первого порядка может быть сведена к дифференциальному уравнению второго порядка относительно комплексной амплитуды либо тока 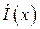, либо напряжения 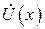путем исключения второй неизвестной. Для рассматриваемых далее однородных линий эти уравнения имеют вид:

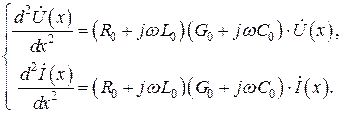(3)

Входящая в уравнения (3) комплексная величина 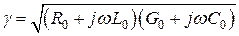носит название комплексного коэффициентом распространения волны в линии.

Рассмотрим одно из дифференциальных уравнений системы (3), например, для напряжения. Общее решение данного линейного однородного дифференциального уравнения второго порядка может быть записано с помощью корней характеристического уравнения ( ):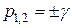

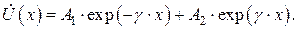(4)

Подставляя данное решение в первое уравнение системы (2), получим:

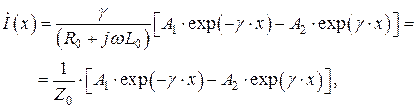(5)

где 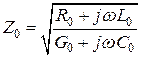- волновое сопротивление длинной линии.

Как видно из полученных выражений, напряжение и ток в любом сечении можно трактовать как суперпозицию двух волн: падающей и отраженной. Первое слагаемое, пропорциональное 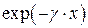, описывает падающую волну, распространяющуюся от генератора к нагрузке (в сторону увеличения координаты 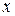). Второе слагаемое, пропорциональное 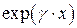, описывает отраженную волну, распространяющуюся от нагрузки к генератору (в сторону уменьшения координаты ).

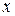Представление комплексного коэффициента распространения в алгебраической форме записи 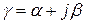приводит к понятиям коэффициента затухания 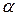и коэффициента фазы 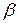. Коэффициент затухания описывает уменьшение амплитуды волны по мере ее распространении в линии, а коэффициент фазы – изменение начальной фазы волны по мере ее распространении в линии.[9]

Из выражения (5) следует, что величина 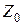описывает связь между амплитудами тока и напряжения, как в падающей, так и в отраженной волнах. Именно поэтому данная величина называется волновым сопротивлением[10].

Величины 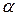, 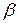и 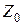носят называние вторичных параметров длинной линии.

Введем параметры волны, распространяющейся в длинной линии. Для этого запишем мгновенное значение напряжения в падающей и отраженной волнах:

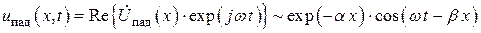, (6а)

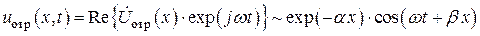, (6б)

где 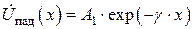и 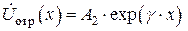- комплексные амплитуды напряжения в падающей и отраженной волнах в сечении длинной линии с координатой .

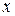Тогда длина волны 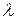в линии, определяемая как расстояние между двумя сечениями линии, фаза волны в которых отличается на 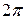рад:

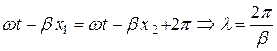. (7)

Введем понятие фазовой скорости. Фазовой скоростью[11] 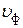назовем скорость движения фронта волны, фаза которого остается постоянной. Тогда, исходя из того, что 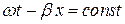для падающей волны и 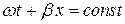для отраженной волны, получаем:

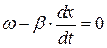, или 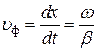; (8а)

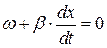, или 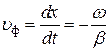. (8б)

Из полученных выражений видно, что падающая и отраженная волны характеризуются одной и той же фазовой скоростью (знак минус указывает лишь на направление движения фронта волны).

Длинная линия без искажений

Гармонический сигнал представляет собой лишь простейший вид переменных сигналов, передаваемых по линиям электропередачи. Часто оказывается, что форма передаваемого сигнала сложнее и сигнал может быть представлен суммой множества гармонических составляющих. При передаче такого сигнала вдоль длинной линии могут наблюдаться нелинейные искажения сигнала. Если амплитуда каждой из составляющих будет уменьшаться с различной интенсивностью, то возникнут так называемые амплитудные искажения, а если будут различаться временные сдвиги гармонических составляющих, то возникнут фазовые искажения.

Для того чтобы при передаче сигнала сложной формы посредством длинной линии отсутствовали нелинейные искажения достаточно, чтобы коэффициент затухания не зависел от частоты, а коэффициент фазы был бы прямо пропорционален частоте:

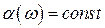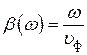, , (9)

где 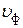не зависит от частоты. Ограничения (9) представляют собой условия неискаженной передачи сигнала.

Данные условия будут автоматически выполняться, если для первичных параметров длинной линии справедливо соотношение[12]:

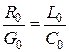. (10)

Действительно, в этом случае комплексный коэффициент распространения волны в линии:

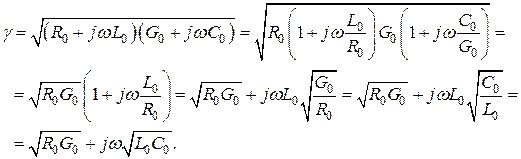(11)

Таким образом, коэффициент затухания равен 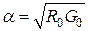и не зависит от частоты, а коэффициент фазы равен 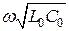и прямо пропорционален частоте. Длинные линии, для которых выполняется условие (10) носят название линий без искажений.

На практике условие (10) без принятия специальных мер не выполняется и всегда:

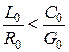. (12)

Для того чтобы неравенство (12) перешло в равенство (9) на практике, обычно, искусственно увеличивают параметр 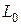, включая через определенные промежутки в линию катушки индуктивности.