Тема 1.2. парная линейная регрессия
И КОРРЕЛЯЦИЯ
План лекции
1. Модель линейной парной регрессии. Метод наименьших квадратов.
2. Коэффициент корреляции.
3. Основные положения регрессионного анализа. Теорема Гаусса – Маркова.
4. Оценка значимости уравнения регрессии. Коэффициент детерминации.
5. Построение интервальных прогнозов по модели парной регрессии.
Введение
В экономике в большинстве случаев между переменными величинами существуют зависимости, когда каждому значению одной переменной соответствует множество возможных значений другой переменной. Иначе говоря, каждому значению одной переменной соответствует определенное (условное) распределение другой переменной. Такая зависимость получила название статистической.
В силу неоднозначности статистической зависимости между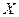 
и 
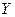для исследователя, в частности, представляет интерес усредненная по 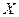схема зависимости. Если зависимость между двумя переменными такова, что каждому значению одной переменной соответствует определенное условное математическое ожидание (среднее значение) другой, то такая статистическая зависимость называется корреляционной. Корреляционная зависимость может быть представлена в виде
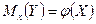или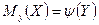 
.
В регрессионном анализе рассматриваются односторонняя зависимость случайной переменной 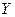от одной (или нескольких) неслучайной независимой переменной 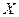. Такая зависимость может возникнуть, например, в случае, когда при каждом фиксированном значении 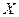соответствующие значения 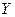подвержены случайному разбросу за счет действия ряда неконтролируемых факторов.
Зависимость такого типа, выражаемая соотношением
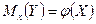(2.1)
называется функцией регрессии 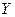на 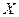. При этом 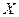называется независимой (объясняющей) переменной (регрессором), 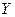– зависимой (объясняемой) переменной. При рассмотрении зависимости двух случайных величин говорят о парной регрессии.
В статистической практике исследователь располагает лишь выборкой пар значений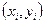 
ограниченного объема п. В этом случае речь может идти об оценке (о приближенном выражении) по выборке функции регрессии. Такой оценкой является выборочное уравнение регрессии:
,
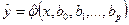где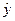 
– условная (групповая) средняя переменной 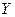при фиксированном значении переменной 
; 
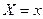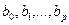– параметры регрессии.
При правильно определенной аппроксимирующей функции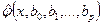 
с увеличением объема выборки 
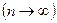она будет сходиться по вероятности к функции регрессии 
.
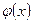Модель линейной парной регрессии.
Метод наименьших квадратов
Если функция регрессии линейна, то говорят, о линейной регрессии.
Линейная регрессия находит широкое применение в эконометрике ввиду четкой экономической интерпретации ее параметров.
Линейная регрессия сводится к нахождению уравнения вида
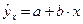или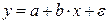 
. (2.2)
Уравнение вида 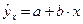позволяет по заданным значениям фактора 
иметь теоретические знания результативного признака подстановкой в него фактических значений фактора .
Построение линейной регрессии сводится к оценке ее параметров – 
и 
. Оценки параметров линейной регрессии могут быть найдены разными методами.
Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).
Метод наименьших квадратов позволяет получить такие оценки параметров и , при которых сумма квадратов отклонений фактических значений результативного признака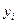 
от расчетных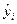 
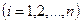минимальна:
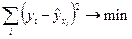(2.3)
Иными словами, из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной:
,
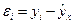следовательно,
.
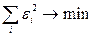Для того чтобы найти минимум функции (2.3), надо вычислить частные производные по каждому из параметров и и приравнять их к нулю.
Обозначим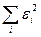 
через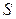 
, тогда:
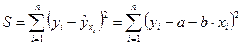
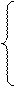
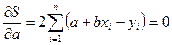
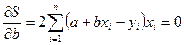(2.4)
Преобразуя формулу (2.4), получим следующую систему нормальных уравнений для оценки параметров и :
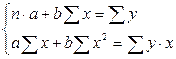(2.5)
Теперь, разделив обе части уравнений (2.5) на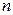 
, получим систему нормальных уравнений в виде:
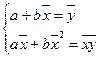, (2.6)
где соответствующие средние определяются по формулам:
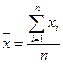, (2.7)
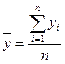, (2.8)
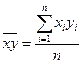, (2.9)
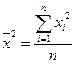. (2.10)
Подставляя значение
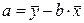(2.11)
из первого уравнения системы (2.6) в уравнение регрессии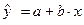 
, получим
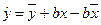
или
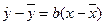. (2.12)
Решая систему нормальных уравнений (2.5) либо методом последовательного исключения переменных, либо по формулам Крамера, найдем искомые оценки параметров и .
Поскольку ковариация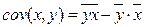 
, а дисперсия признака Х 
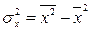, получим следующую формулу расчета оценки параметра :
= 
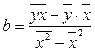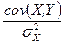(2.13)
Параметр называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Так, если функция издержек (У, тыс. руб.) выражается как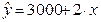 
, ( – количество единиц продукции), то, следовательно, с увеличением объема продукции на одну единицу издержки производства возрастают в среднем на 2 тыс. руб., т.е. дополнительный прирост продукции на одну единицу потребует увеличения затрат в среднем на 2 тыс. руб.
Знак при коэффициенте регрессии показывает направление связи: при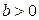 
– связь прямая, а при 
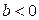– связь обратная.
Параметр может не иметь экономического содержания.
Пример 1.
По группе предприятий выпускающих один и тот же вид продукции, рассматривается функция издержек 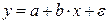. Необходимая для расчета оценок параметров и информация представлена в таблице.
| Расчетная таблица | ||||||
| Номер предприятия | Выпуск продукции, тыс. ед. | Затраты на производство, млн. руб.  |  |  |  |  |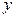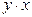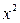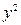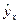
| 31,1 | ||||||
| 67,9 | ||||||
| 141,6 | ||||||
| 104,7 | ||||||
| 178,4 | ||||||
| 104,7 | ||||||
| 141,6 | ||||||
| Итого |
Система нормальных уравнений будет иметь вид:
.
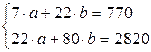Решив ее, получим:
.
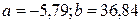Запишем уравнение регрессии:
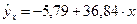
Подставив в уравнение значения , найдем теоретические значения 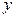(см. последнюю графу таблицы). В данном случае величина параметра не имеет экономического смысла.
В рассматриваемом примере имеем:
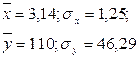
Коэффициент корреляции
Перейдем к оценке тесноты корреляционной зависимости. Рассмотрим наиболее важный для практики и теории случай линейной зависимости вида .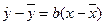
Представим уравнение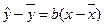 
в эквивалентном виде:
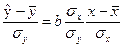
В этой системе величина
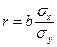(2.14)
показывает, на сколько величин sу изменится в среднем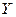 
, когда 
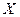увеличится на одно sх.
Величина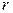 
является показателем тесноты линейной связи и называется выборочным коэффициентом корреляции (или просто коэффициентом корреляции).
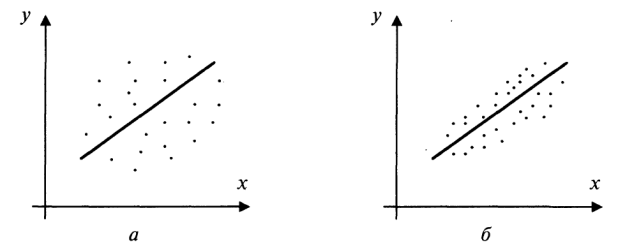
Две корреляционные зависимости переменной 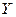от 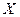приведены на рис. Очевидно, что в случае а) зависимость между переменными менее тесная и коэффициент корреляции должен быть меньше, чем в случае б), так как точки корреляционного поля а) дальше отстоят от линии регрессии, чем точки поля б).
Если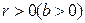 
, то корреляционная связь между переменными называется прямой, если 
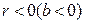, - обратной. При прямой (обратной) связи увеличение одной из переменных ведет к увеличению (уменьшению) условной (групповой) средней другой.
Учитывая (2.13), формулу для 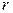представим в виде:
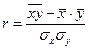(2.15)
Отметим другие модификации формулы 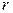, полученные из формулы (2.15):
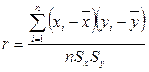(2.16)
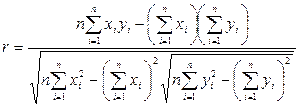(2.17)
Для практических расчетов наиболее удобна формула (2.17), так как по ней 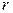находится непосредственно из данных наблюдений и на значении 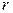не скажутся округления данных, связанные с расчетом средних и отклонений от них.
Выборочный коэффициент корреляции 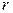(при достаточно большом объеме выборки 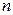) так же, как и коэффициент корреляции двух случайных величин, обладает следующими свойствами.
1. Коэффициент корреляции принимает значения на отрезке [– 1;1], т.е.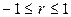 
. Чем ближе 
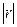к единице, тем теснее связь.
2. При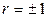 
корреляционная связь представляет линейную функциональную зависимость. При этом все наблюдаемые значения располагаются на прямой линии.
3. При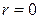 
линейная корреляционная связь отсутствует. при этом линия регрессии параллельна оси Ох.