Основные положения регрессионного анализа.

Теорема Гаусса – Маркова

В силу воздействия неучтенных случайных факторов и причин отдельные наблюдения переменной 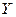будут в большей или меньшей мере отклоняться от функции регрессии .

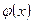Рассмотрим линейный регрессионный анализ, для которого линейная парная регрессионная модель имеет вид:

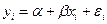. (2.18)

Отметим основные предпосылки регрессионного анализа.

1. В модели 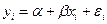возмущение 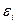(или зависимая переменная 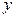) есть величина случайная, а объясняющая переменная 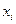- величина неслучайная.

2. Математическое ожидание возмущения 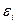равно нулю:

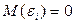(2.19)

(или математическое ожидание зависимой переменной 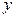равно линейной функции регрессии: ).

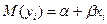3. Дисперсия возмущения 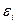(или зависимой переменной 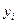) постоянна для любого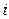

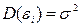(2.20)

(или 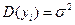) – условие гомоскедастичности или равноизменчивости возмущения (зависимой переменной )).

4. Возмущения 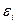и (и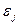ли переменные 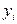и 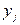) не коррелированы:

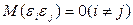(2.21)

5. Возмущение 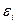(или зависимая переменная 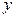) есть нормально распределенная случайная величина.

В этом случае модель 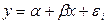называется классической нормальной линейной регрессионной моделью.

Для получения уравнения регрессии достаточно предпосылок 1 – 4. Требование выполнения предпосылки 5 (т.е. рассмотрение «нормальной регрессии») необходимо для оценки точности уравнения регрессии и его параметров.

Оценкой модели 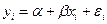по выборке является уравнение регрессии 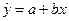. Параметры этого уравнения и определяются на основе метода наименьших квадратов.

Воздействие неучтенных случайных факторов и ошибок наблюдений в модели 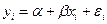определяется с помощью дисперсии возмущений (ошибок) или остаточной дисперсии 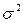. Несмещенной оценкой этой дисперсии является выборочная остаточная дисперсия.

S ² 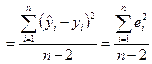, (2.22)

где 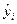– групповая средняя, найденная по уравнению регрессии; 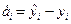– выборочная оценка возмущения 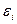или остаток регрессии.

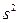Возникает вопрос, являются ли оценки , и параметров 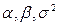«наилучшими»? Ответ на этот вопрос дает следующая теорема.

Теорема Гаусса – Маркова. Если регрессионная модель 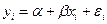удовлетворяет предпосылкам 1 – 4, то оценки , имеют наименьшую дисперсию в классе всех линейных несмещенных оценок.

Таким образом, оценки , в определенном смысле являются наиболее эффективными линейными оценками параметров , .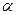

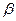Оценка значимости уравнения регрессии.

Коэффициент детерминации

Проверить значимость уравнения регрессии – значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной.

Проверка значимости уравнения регрессии производится на основе дисперсионного анализа.

В математической статистике дисперсионный анализ рассмотрен как самостоятельный инструмент (метод) статистического анализа. Здесь же он применяется как вспомогательное средство для изучения качества регрессионной модели.

Согласно основной идее дисперсионного анализа общая сумма квадратов отклонений зависимой переменной от средней 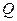представляется в виде:

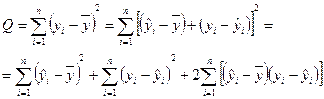(2.23)

или 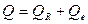, (2.24)

где 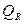и 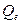– соответственно сумма квадратов, обусловленная регрессией, и остаточная сумма квадратов, характеризующая влияние неучтенных факторов и

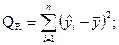
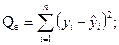(2.24)

Легко убедиться в том, что в (2.23) третье слагаемое 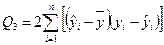равно 0 (см. [1], с.70).

Схема дисперсионного анализа имеет вид, представленный в таблице.

Компоненты регрессии	Сумма квадратов	Число степеней свободы	Средние квадраты
Регрессия		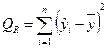m – 1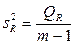
Остаточная		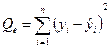n – m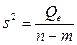
Общая		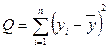n – 1

Средние квадраты 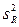, 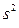представляют собой несмещенные оценки дисперсий зависимой переменной, обусловленных соответственно регрессией или объясняющей переменной 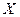и воздействием неучтенных случайных факторов и ошибок; m – число оцениваемых параметров уравнения регрессии; n – число наблюдений.

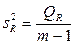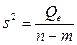При отсутствии линейной зависимости между зависимой и объясняющими(ей) переменными случайные величины и имеют 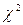– распределение соответственно с m – 1 и n – m степенями свободы, а их отношение – 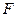-распределение с теми же степенями свободы. Поэтому уравнение регрессии значимо на уровне 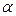, если фактически наблюдаемое значение статистики

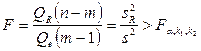, (2.24)

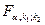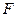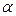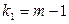где – табличное значение -критерия Фишера-Снедекора, определенное на уровне значимости при и 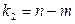степенях свободы.

Учитывая смысл величин 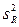и 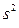, можно сказать, что значение 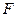показывает, в какой мере регрессия лучше оценивает значение зависимой переменной по сравнению с ее средней.

В случае линейной парной регрессии 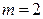, и уравнение регрессии значимо на уровне 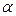, если

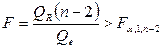. (2.25)

Иначе, гипотеза 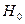о равенстве параметра нулю, т.е. 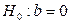, отвергается.

Одной из наиболее эффективных оценок адекватности регрессионной модели, мерой качества уравнения регрессии, (или, как говорят, мерой качества подгонки регрессионной модели к наблюденным значениям 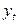), характеристикой прогностической силы анализируемой регрессионной модели является коэффициент детерминации, определяемый по формуле:

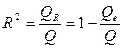. (2.26)

Величина 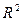показывает, какая часть (доля) вариации зависимой переменной обусловлена вариацией объясняющей переменной.

Так как 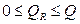, то .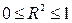

Чем ближе 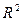к единице, тем лучше регрессия аппроксимирует эмпирические данные, тем теснее наблюдения примыкают к линии регрессии. Если 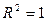, то эмпирические точки 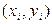лежат на линии регрессии и между переменным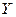и и 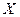существует линейная функциональная зависимость. Если 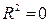, то вариация зависимой переменной полностью обусловлена воздействием неучтенных в модели переменных, и линия регрессии параллельна оси абсцисс.

Если известен коэффициент детерминации 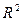, то критерий значимости (2.24) уравнения регрессии или самого коэффициента детерминации может быть записан в виде:

.

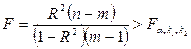В случае парной линейной регрессионной модели коэффициент детерминации равен квадрату коэффициента корреляции, т.е. 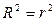.