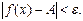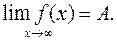Линейные операции над векторами.
Суммой a + b векторовa и b называется вектор, идущий из начала вектора а в конец вектора b, если начало вектора b совпадает с концом вектора а.
Такое правило сложения векторов называют правилом треугольника.
Рис.3. Сложение векторов по правилу треугольника.
Существует еще одно правило сложения векторов – правило параллелограмма: суммавекторов a и b есть диагональ параллелограмма, построенного на них как на сторонах, выходящая из их общего начала.
Рис.4. Сложение векторов по правилу параллелограмма.
Разностью а – bвекторов а и bназывается такой вектор с, который в сумме с вектором bдает вектор а.
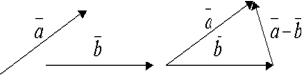
Рис.4. Вычитание векторов.
Произведениемkaвектора а на число k называется вектор b, коллинеарный векторуа, имеющий модуль, равный |k||a|, и направление, совпадающее с направлением апри k>0 и противоположное а при k<0.
Если векторы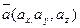 
и 
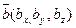заданы своими координатами, то их сумма и разность определяются по формулам:
;
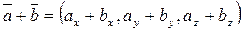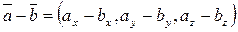
Произведение вектора на число определяется формулой
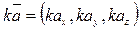
Вектор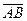 
, имеющий начало в точке 
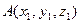и 
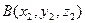, определяется через координаты точек А и В:
.
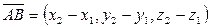Скалярное произведение векторов Скалярным произведением двух векторов называется произведение их модулей на косинус угла между ними:ab = |a||b| cosφ. Обозначается скалярное произведение: ab, (ab), a·b .
Свойства скалярного произведения:
1. ab = ba .
2. (ka)b = k(ab).
3. (a + b)c = ac + bc .
4. a2 = aa = |a|2 , где а2 называется скалярным квадратом вектора а.
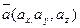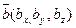Если векторы а и b определены своими координатами и ,то
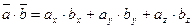
Отметим условия коллинеарности и перпендикулярности двух не нулевых векторов:
|| 
┴ 
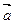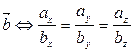
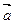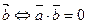
Пример 1. Найти длину вектора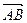 
по заданным координатам его концов 
, 
.
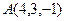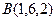Решение:
Находим координаты вектора :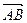 
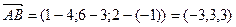, а теперь найдем модуль этого вектора: 
.
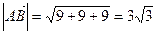Пример 2.Даны векторы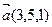 
, 
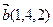и 
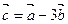. Определить длину вектора 
.
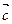Решение:
Найдем координаты вектора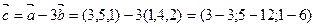 
. Итак, 
.
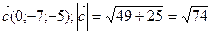Пример 3.Найти косинус угла между векторам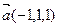и 
и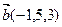 
.
Решение:
Из определения скалярного произведения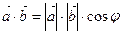 
следует, что 
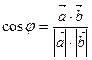. По координатам векторов находим: 
,
; 
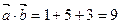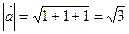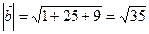, поэтому 
.
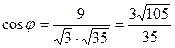Пример 4.Доказать, что диагонали четырехугольника, заданного координатами вершин А(-4;-4;4), В(-;2;2), С(2;5;1), D(3;-2;2), взаимно перпендикулярны.
Решение:
Составим вектора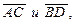 
лежащие на диагоналях данного четырёхугольника. Имеем:
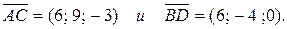
Проверим, ортогональны ли эти вектора. Для этого найдём их скалярное произведение:
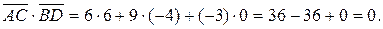
Отсюда следует, что вектора, лежащие на диагоналях четырёхугольника ортогональны, а значит, диагонали взаимно перпендикулярны и данный четырёхугольник является параллелограммом
Задания для самостоятельной работы
1. Вычислите скалярное произведение векторов:
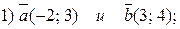
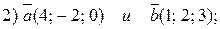
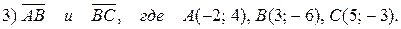
2. Ортогональны ли векторы (проверить с помощью скалярного произведения):
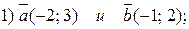
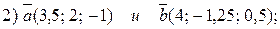
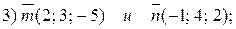
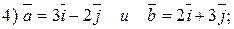
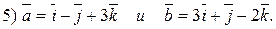
3. Найдите угол между векторами, используя таблицу Брадиса:
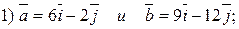
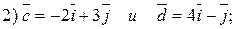
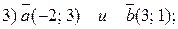
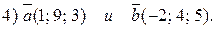
Рекомендуемая литература: 1.1[с. 228-229], 1.2[с. 268-283], 2.1[с. 44-45].
Самостоятельная работа №4
Тема: Кривые второго порядка
Цель: формирование умения составления уравнений кривых второго порядка.
Время выполнения: 6 часов.
Теоретический материал
Если Р(х; у) многочлен второй степени, то линии, определяемые уравнением.
Р(х; у)=0 (1),
называются линиями второго порядка, а уравнение (1) может быть записано в виде
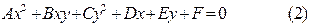
Линия второго порядка, задаваемая уравнением (2) в зависимости от коэффициентов А, В, С, D, Е, F, определяет эллипс, гиперболу или параболу, а при некоторых значениях коэффициентов - точку или две прямые (последние случаи называют вырожденными).
Окружностью радиуса R с центром в точке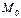 
называется множество всех точек М плоскости, удовлетворяющих условию 
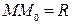(см. рис.5).
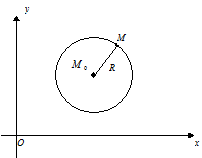
Рис. 5. Окружность со смещенным центром.
Каноническое уравнение окружности имеет вид:
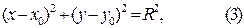
где х и у – текущие координаты,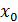 
и 
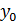- координаты центра окружности, R – радиус окружности.
В частности, если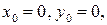 
получим каноническое уравнение окружности с центром в начале координат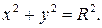 
Как было сказано выше, окружность является линией второго порядка, следовательно, её уравнение тоже можно рассматривать как частный случай уравнения (2).
Если мы раскроем скобки в уравнении (3), то после некоторых преобразований мы получим уравнение вида
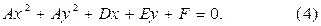
Мы видим, что уравнение (4) отличается от уравнения (2) только тем, что член, содержащий произведение ху, отсутствует.
Таким образом, окружность определяется общим уравнением второй степени с двумя переменными, если в нём коэффициенты при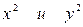 
равны между собой и отсутствует член с произведением ху.
Эллипсом называется множество точек плоскости, декартовы координаты которых удовлетворяют уравнению:
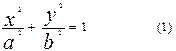
Числа а и b - полуоси эллипса.
Эллипс - это линия, симметричная относительно осей Ох и Оу.
Точки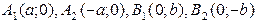 
называются вершинами эллипса.
Из канонического уравнения эллипса мы можем вывести формулы для вычисления х и у:
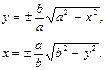
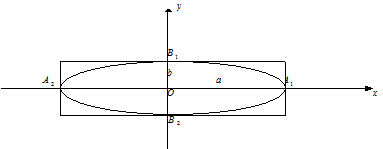
Рис. 6. Эллипс.
Гиперболой называется множество точек плоскости, декартовы координаты, которых удовлетворяют уравнению:
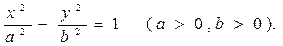
Из канонического уравнения гиперболы выводим уравнения х и у:
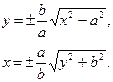
Гипербола состоит из двух частей, называемых ветвями.
При a=b гипербола называется равносторонней (равнобочной) и её уравнение имеет вид
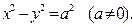
Гипербола, заданная уравнением вида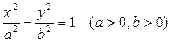 
имеет вид: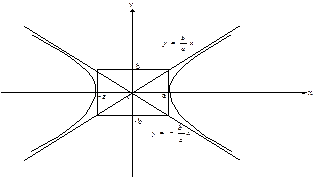 
Рис.7. Гипербола.
Гипербола, заданная уравнением вида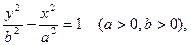 
называется сопряжённой гиперболе 
.
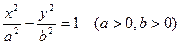Центром гиперболы является начало координат. Точки пересечения гиперболы с осями симметрии называются вершинами гиперболы.
Числа a ,b –полуосями.
Прямые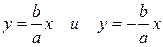 
являются асимптотами гиперболы.
Задания для самостоятельной работы
Таблица 1
| Номер задачи | Текст задачи |
1. Составить уравнение гиперболы с фокусами на оси Ох, если расстояние между ее фокусами равно 20, а уравнение ее асимптот 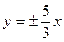 . 2. Составить уравнение директрисы параболы у2-4у-12х+16=0. | |
| 1. Составить уравнение эллипса с фокусами на оси Ох, если расстояние между фокусами равно16, а эксцентриситет равен ½. 2. Составить уравнение оси параболы у2-6у-12х-15=0. | |
| 1. Составить уравнение эллипса с фокусами на оси Ох, если расстояние между фокусами равно12, а эксцентриситет равен 3/10. 2. Составить уравнение оси параболы у2+6у-8х+1=0. | |
1. Составить уравнение эллипса с фокусами на оси Ох, проходящего через точки А(6;4) и В( 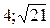 ). 2. Составить уравнение директрисы параболы у2+8у+28х+72=0. | |
1. Составить уравнение эллипса с фокусами на оси Ох, проходящего через точк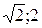и (  ) и ( 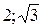 ). 2. Составить уравнение оси параболы у2-4у-16х+52=0. | |
1. Найти эксцентриситет эллипса 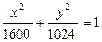 . 2. Составить уравнение оси параболы Х 2 +8х+16у+48=0. | |
1. Найти эксцентриситет гиперболы 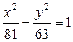 . 2. Составить уравнение директрисы параболы Х 2 +8х-28у+44=0. | |
1. Дан эллипс 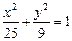 . Найти его полуоси и расстояние между фокусами. 2. Написать уравнение гиперболы, проходящей через точку (2;1) , асимптоты которой  . | |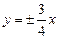
1. Дана гипербола 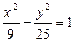 . Найти ее оси и расстояние между фокусами. 2. Написать уравнение параболы с вершиной в начале координат, если координаты фокуса равны F(0;-5). | |
| 1. Найти эксцентриситет эллипса 4х2+9у2=180. 2. Написать уравнение директрисы и найти координаты фокуса параболы У2=4х. |
Рекомендуемая литература: 1.1[с. 309-317], 1.2[с. 304-326], 2.1[с. 25-30].
Самостоятельная работа №5
Тема: Теория пределов
Цель: формирование умения доказывать основные положения и теоремы теории пределов.
Время выполнения:6 часов (для 09.02.03, 09.02.04), 10 часов для (09.02.01)
Теоретический материал
Пусть функция f(x) определена в некоторой окрестности точки х=а, кроме, может быть самой точки а.
Число А называется пределом функции f(x) при стремлении х к а (или в точке а), если для любого числа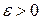 
существует такое число 
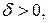что для всех 
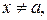удовлетворяющих условию 
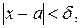имеет место неравенство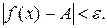 
Обозначают: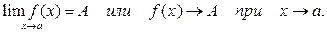 
Из определения следует, что, если число А есть предел функции f(x) в точке х=а, то для всех х, достаточно близких к числу а и отличных от него соответствующие им значения функции f(x) оказываются сколь угодно близкими к числу А.
Число А называется пределом функции f(x) при стремлении х к бесконечности, если для любого числа 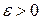существует такое положительное число N, что для всех х удовлетворяющих условию 
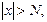имеет место неравенство 
