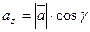Решение систем линейных уравнений методом Гаусса
Элементарные преобразования матриц:
- перестановка местами двух параллельных рядов матрицы;
- умножение всех элементов ряда матрицы на число, отличное от нуля;
- прибавление к элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.
Две матрицы А и В называются эквивалентными, если одна из них получается из другой с помощью элементарных преобразований. Записывается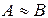 
.
Расширенной матрицей назовём следующую матрицу:
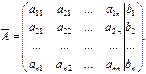
С помощью элементарных преобразований матрицу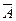 
по методу Гаусса можно привести к виду:
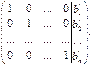Тогда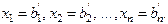 
Для формализации преобразования матрицы 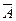введём правило прямоугольника.
Рассмотрим прямоугольник из 4-ёх элементов матрицы :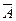
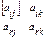
Назовём элемент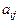 
ведущим, строку, в которой он стоит - ведущей строкой. По правилу прямоугольника пересчитывается элемент, стоящий по диагонали от ведущего элемента по следующей формуле:
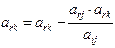
Очевидно, что формула упростится, если ведущий элемент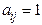 
. Поэтому, если в системе есть элементы равные 1, то их рекомендуется выбирать ведущими.
Для проверки верности счёта к расширенной матрице приписывается столбец сумм, элементы которого равны построчным суммам матрицы 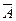. Над элементами контрольного столбца производятся те же операции, что и над элементами матрицы 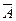. Если сумма строки равна соответствующему элементу контрольного столбца, рассчитанного по правилу прямоугольника, то счёт ведётся верно, в противном случае следует искать ошибку в счёте.
Пример 3.Решить систему уравнений:
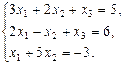
Решение:
Выпишем матрицу 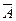; припишем к ней контрольный столбец.
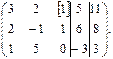
За ведущий элемент примем 1, стоящую в первой строке и 3–ем столбце (Ведущими можно выбирать только элементы основной матрицы, т.е. матрицы без столбца свободных членов). Ведущую строку перепишем без изменения, в ведущем столбце запишем нули, все остальные элементы пересчитаем по правилу прямоугольника:
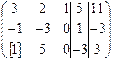, т.е.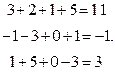 
Пример пересчёта элемента 2, стоящего во второй строке и первом столбце:
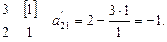
Пример пересчёта элемента -1, стоящего во второй строке и втором столбце:
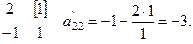
Далее примем за ведущий элемент единицу, стоящую в третьей строке и первом столбце. Третью строку и третий столбец перепишем без изменения, в первом столбце запишем нули, остальные элементы пересчитаем по правилу прямоугольника:
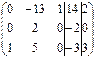, т.е.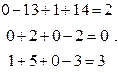 
Разделим вторую строку на 2 (это равносильно делению обеих частей уравнения на 2), получим
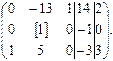
Выбираем ведущей 1, стоящую во второй строке и втором столбце (заметим, что строка и столбец могут быть ведущими только 1 раз).
Вторую строку, первый и третий столбцы переписываем без изменения, во втором столбце записываем нули, остальные элементы пересчитываем по правилу прямоугольника.
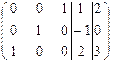, т.е.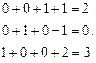 
Таким образом, получили ответ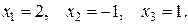 
Задания для самостоятельной работы
1. Решить систему линейных уравнений используя правило Крамера и матричный способ
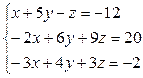
2. Решить систему линейных уравнений используя метод Гаусса:
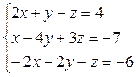
Рекомендуемая литература: 1.1[с.7-10], 1.2[с.11-12], 2.1[с. 88-89].
Самостоятельная работа №3
Тема: Операции над векторами. Вычисление скалярного произведения через координаты векторов
Цель:закрепление умения производить действия над векторами в координатной и геометрической форме. Находить координаты вектора, модуль вектора, скалярное произведение векторов через координаты
Время выполнения: 4 часа
Теоретический материал
Вектором называется направленный отрезок. Обозначения: a,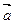 
, 
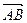
Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Вектор называется нулевым, если его начальная и конечная точки совпадают. Нулевой вектор не имеет определенного направления.
Два вектора называются равными, если они коллинеарны, имеют одинаковую длину (модуль) и одинаковое направление.
Проекциейвектора АВ на ось OX (OY) называется длина направленного отрезка А/В/ оси OX (OY), где А/ и В/ - основания перпендикуляров, опущенных из точек А и В на ось OX (OY).
Проекции вектора на координатные оси – координаты вектора: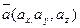 
. Длина вектора находится по формуле
.
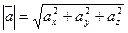Пусть α, β, γ – углы, образованные вектором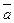 
с осями координат (Ox, Oy, Oz соответственно), тогда
, 
, 
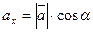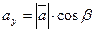