Бесконечно малые и бесконечно большие величины
Бесконечно малая величина
Функция 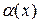 называется бесконечно малой при
называется бесконечно малой при 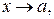 если
если 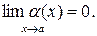
Свойства бесконечно малой величины
1. Если функции 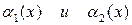 являются бесконечно малыми, то
являются бесконечно малыми, то 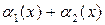 также есть бесконечно малая.
также есть бесконечно малая.
2. Произведение ограниченной при 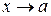 функции на бесконечно малую есть бесконечно малая.
функции на бесконечно малую есть бесконечно малая.
3. Произведение постоянной на бесконечно малую есть бесконечно малая.
4. Произведение двух бесконечно малых есть бесконечно малая.
Бесконечно большая величина
Функция f(x) называется бесконечно большой при 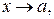 если
если 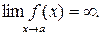
Свойства бесконечно больших величин
1. Если функция f(x) бесконечно большая, то 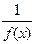 бесконечно малая.
бесконечно малая.
2. Если функция 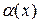 бесконечно малая и не обращается в нуль, то
бесконечно малая и не обращается в нуль, то 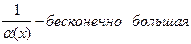
Основные теоремы о пределах
Теорема 1. Предел постоянной равен самой постоянной.
Теорема 2. Если функции f(x) u g(x)имеют пределы при 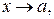 то при
то при 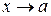 имеют пределы также их сумма f(x) + g(x), произведение
имеют пределы также их сумма f(x) + g(x), произведение 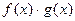 и при условии, что
и при условии, что
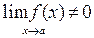 частное
частное 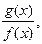 причём
причём
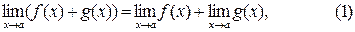
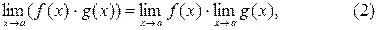
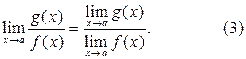
Следствие 1. Если функция f(x) имеет предел при 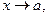 то
то
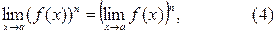 где n – натуральное число.
где n – натуральное число.
Следствие 2. Постоянный множитель можно выносить за знак предела:
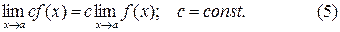
Задание для самостоятельной работы
Самостоятельная работа выполняется по вариантам. Каждый обучащийся вместо букв n и k ставит свои числа, где n – количество букв фамилии, k – количество букв полного имени. (Например: Иванов Федор – n=6, k=5)
Задание. Вычислить пределы
1. 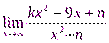 2.
2. 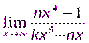 3.
3. 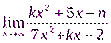 4.
4. 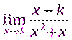
5. 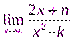 6.
6. 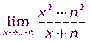 7.
7. 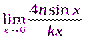 8.
8. 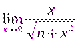
9. 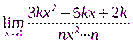
Рекомендуемая литература: 1.1[с. 193-208], 1.2[с. 71-87], 2.1[с.142-149].
Самостоятельная работа №6
Тема: Дифференциальное исчисление функции одной действительной переменной.
Цель: закрепление и систематизация знаний по теме «Производная и дифференциал функции».
Время выполнения: 6 часов (для 09.02.03, 09.02.04),10 часов для (09.02.01)
Теоретический материал
Пусть функция y=f(x) определена в промежутке (a;b). Возьмём какое-нибудь значение х из (a;b). Затем возьмём новое значение аргумента 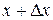 из этого промежутка, придав первоначальному значению х приращение
из этого промежутка, придав первоначальному значению х приращение 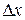 (положительное или отрицательное).
(положительное или отрицательное).
Этому новому значению аргумента соответствует и новое значение функции
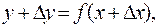 где
где 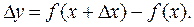
Теперь составим отношение
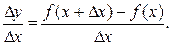 Оно является функцией от
Оно является функцией от 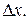
Если существует предел отношения 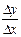 приращения функции
приращения функции 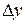 к вызвавшему его приращению аргумента
к вызвавшему его приращению аргумента 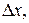 когда
когда 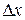 стремится к нулю, то этот предел называется производной от функции y=f(x) в данной точке х и обозначается через y’ или f’(x) (читается «игрек штрих» или «эф штрих от икс»):
стремится к нулю, то этот предел называется производной от функции y=f(x) в данной точке х и обозначается через y’ или f’(x) (читается «игрек штрих» или «эф штрих от икс»):
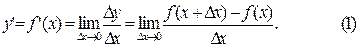
Для обозначения производной принят также и следующий символ 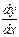 (читается «дэ игрек по дэ икс»). Эту запись надо рассматривать пока как целый символ, а не как частное.
(читается «дэ игрек по дэ икс»). Эту запись надо рассматривать пока как целый символ, а не как частное.
Действие нахождение производной называется дифференцированием, а функцию, имеющую производную в точке х, называют дифференцируемой в этой точке.
Функция, дифференцируемая в каждой точке промежутка, называется дифференцируемой в этом промежутке.
Задание для самостоятельной работы
Подготовить презентацию или сообщение на тему:
1) Задачи, приводящие к понятию производной.
2) Производная, ее геометрический и механический смысл.
Рекомендуемая литература: 1.1[с. 250-254], 1.2[с.180-184].
Самостоятельная работа №7
Тема: Вычисление собственных и несобственных интегралов
Цель: формирование умения вычислять несобственные интегралы с помощью формулы Ньютона-Лейбница.
Время выполнения: 5 часов (для 09.02.03, 09.02.04), 6 часов для (09.02.01)
Теоретический материал
При рассмотрении определённых интегралов мы предполагали, что область интегрирования ограничена (более конкретно, является отрезком [a,b]); для существования определённого интеграла 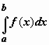 необходима ограниченность подынтегральной функции на [a,b].
необходима ограниченность подынтегральной функции на [a,b].
Будем называть определённые интегралы, для которых выполняются оба эти условия собственными; интегралы, для которых нарушаются эти требования (т.е. неограниченна либо подынтегральная функция, либо область интегрирования, либо и то, и другое вместе) несобственными.
