Преподаватель высшей квалификационной категории
Колледж информатики и связи
Отделение информационных технологий
и вычислительной техники
ЭЛЕМЕНТЫ ВЫСШЕЙ МАТЕМАТИКИ
Методические указания по выполнению самостоятельных работ
по дисциплине «Элементы высшей математики»
для студентов, обучающихся по специальностям:
09.02.01 Компьютерные системы и комплексы
09.02.03 Программирование в компьютерных системах
09.02.04 Информационные системы (по отраслям)
Составитель Т.А.Петрова,
Преподаватель высшей квалификационной категории
Тюмень
ТюмГНГУ
2016
Элементы высшей математики: метод. указ. по выполнению самостоятельных работ для студентов, обучающихся по спец. 09.02.01 Компьютерные системы и комплексы, 09.02.03 Программирование в компьютерных системах, 09.02.04 Информационные системы (по отраслям)/ сост. Т.А.Петрова; Тюменский государственный нефтегазовый университет.– 1-е изд.– Тюмень: Издательский центр БИК, ТюмГНГУ, 2016.– 48 с.
Методические указания рассмотрены и рекомендованы к изданию на заседании цикловой комиссии отделения информационных технологий и вычислительной техники
«20» января 2016 года, протокол № 6
Аннотация
Методические указания по дисциплине «Элементы высшей математики» предназначены для студентов, обучающихся по специальностям: 09.02.01 Компьютерные системы и комплексы, 09.02.03 Программирование в компьютерных системах, 09.02.04 Информационные системы (по отраслям). Данная дисциплина изучается в трех семестрах.
Методические указания состоят из пояснительной записки, описания самостоятельных работ, которые снабжены общими теоретическими сведениями, контрольными вопросами и заданиями в соответствии с программой дисциплины и списка рекомендуемой литературы.
Методические указания по выполнению самостоятельных работ окажут помощь преподавателям в организации самостоятельных работ, а также могут пригодиться обучающимся при повторении изученного материала и подготовке к зачету и экзамену.
СОДЕРЖАНИЕ
  Пояснительная записка Пояснительная записка | |
| Общие требования к оформлению и выполнению самостоятельных работ | |
| Критерии оценки самостоятельных работ | |
| Самостоятельная работа №1. Вычисление определителей матрицы | |
| Самостоятельная работа №2. Решение систем линейных уравнений | |
| Самостоятельная работа №3. Векторы. Координаты векторов | |
| Самостоятельная работа №4. Кривые второго порядка | |
| Самостоятельная работа №5. Теория пределов | |
| Самостоятельная работа №6. Производная и дифференциал функции | |
| Самостоятельная работа №7. Несобственные интегралы | |
| Самостоятельная работа №8. Частные производные функций нескольких действительных переменных | |
| Самостоятельная работа №9. Вычисление двойных интегралов | |
| Самостоятельная работа №10. Решение дифференциальных уравнений | |
| Самостоятельная работа №11. Разложение функций в степенные ряды | |
| Самостоятельная работа №12. Действия над комплексными числами | |
| Список литературы |
Пояснительная записка
 Методические указания по выполнению самостоятельных работ составлены в соответствии с рабочей программой дисциплины «Элементы высшей математики» для специальностей: 09.02.01 Компьютерные системы и комплексы, 09.02.03 Программирование в компьютерных системах, 09.02.04 Информационные системы (по отраслям).
Методические указания по выполнению самостоятельных работ составлены в соответствии с рабочей программой дисциплины «Элементы высшей математики» для специальностей: 09.02.01 Компьютерные системы и комплексы, 09.02.03 Программирование в компьютерных системах, 09.02.04 Информационные системы (по отраслям).
Самостоятельные работы занимают важное место при изучении дисциплины «Элементы высшей математики». Цель выполнения работ – систематизация и закрепление теоретических знаний, формирование умений решения математических задач при помощи различных методов, развитие познавательных способностей и активности обучающихся, ответственности и организованности, формирование самостоятельности мышления.
В результате освоения учебной дисциплины Элементы высшей математики обучающийся должен обладать предусмотренными ФГОС по специальностям: 09.02.01 Компьютерные системы и комплексы, 09.02.03 Программирование в компьютерных системах, 09.02.04 Информационные системы (по отраслям) базовой подготовки следующими умениями, знаниями, которые формируют профессиональные компетенции, и общими компетенциями:
У1 Умение выполнять операции над матрицами и решать системы линейных уравнений.
У2 Умение решать задачи, используя уравнения прямых и кривых второго порядка на плоскости (только для 09.02.03).
У3 Умение применять методы дифференциального и интегрального исчислений.
У4 Умение решать дифференциальные уравнения.
У5 Умение пользоваться понятиями теории комплексных чисел (только для 09.02.03).
З1 Знание основ математического анализа, линейной алгебры и аналитической геометрии.
З2 Знание основ дифференциального и интегрального исчислений.
З3 Знание основ теории комплексных чисел (только для 09.02.03).
В процессе освоения учебной дисциплины обучающийся получит возможность повысить уровень сформированности общих и профессиональных компетенций:
Для 09.02.03:
ПК 1.1 Выполнять разработку спецификаций отдельных компонент
ПК 1.2. Осуществлять разработку кода программного продукта на основе готовых спецификаций на уровне модуля
ПК 2.4 Реализовывать методы и технологии защиты информации в базах данных
ПК 3.4 Осуществлять разработку тестовых наборов и тестовых сценариев
Для 09.02.04*:
ПК 1.1*. Собирать данные для анализа использования и функционирования информационной системы, участвовать в составлении отчетной документации, принимать участие в разработке проектной документации на модификацию информационной системы.
ПК 1.2*. Взаимодействовать со специалистами смежного профиля при разработке методов, средств и технологий применения объектов профессиональной деятельности.
ПК 1.4*. Участвовать в экспериментальном тестировании информационной системы на этапе опытной эксплуатации, фиксировать выявленные ошибки кодирования в разрабатываемых модулях информационной системы.
ПК 2.3*. Применять методики тестирования разрабатываемых приложений.
Для 09.02.01**:
ПК 1.2**. Разрабатывать схемы цифровых устройств на основе интегральных схем разной степени интеграции.
ПК 1.4**. Проводить измерения параметров проектируемых устройств и определять показатели надежности.
ПК 2.2**. Производить тестирование, определение параметров и отладку микропроцессорных систем.
ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.
ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.
ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.
ОК 5. Использовать информационно-коммуникационные технологии в профессиональной деятельности.
ОК 6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.
ОК 7. Брать на себя ответственность за работу членов команды (подчиненных), результат выполнения заданий.
ОК 8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.
ОК 9. Ориентироваться в условиях частой смены технологий в профессиональной деятельности.
Методические указания для самостоятельных работ состоят из пояснительной записки, общих требований к оформлению работ, критериев оценки, описания каждой работы, которые снабжены общими теоретическими сведениями, примерами решения задач и заданиями для самостоятельного решения, ссылками на рекомендуемую литературу.
Видами заданий для внеаудиторной самостоятельной работы в методических указаниях являются в основном решение математических задач, а также подготовка сообщений и презентаций.
Сроки выполнения самостоятельных работ определяются в соответствии с календарно – тематическими планами дисциплины «Элементы высшей математики». На выполнение каждой работы отводится определенное количество часов в соответствии с тематическими планами рабочих программ дисциплин.
Методические указания для самостоятельной работыокажут помощь преподавателям в организации занятий, а также будут необходимы обучающимся при повторении изученного материала и подготовке к зачетам и экзамену.
Общие требования к оформлению и выполнению самостоятельных работ
Форма отчетности:
1) самостоятельные работы требуется выполнять в отдельной тетради для самостоятельных работ;
2) каждая работа должна содержать:
- номер и название самостоятельной работы;
- цель работы;
- условия заданий;
- подробное решение заданий;
- список используемой литературы;
- вывод по цели работы.
Технические требования к оформлению сообщений:
форма листа А 4, шрифт – Times New Roman, размер шрифта основного текста – 14, размер шрифта заголовков – 14, межстрочный интервал – одинарный, поля: левое – 3 см, правое – 2 см, верхнее – 2 см, нижнее – 2 см, нумерация страниц – снизу справа; рекомендуемый объем – 2-3 страницы.
Критерии оценки самостоятельных работ
Для оценки качества успеваемости обучающихся большое значение имеет проверка выполнения ими самостоятельных работ. Выполнение самостоятельных работ позволяет преподавателю определить отношение обучающегося к учебной деятельности, качество усвоения изучаемого материала, наличие пробелов в знаниях, а также степень самостоятельности при выполнении работ.
Самостоятельные работы оцениваются по пятибальной системе:
- оценка «отлично» выставляется тогда, когда из работы ясно, что обучающийся глубоко и прочно освоил программный материал, умеет тесно связывать теорию с практикой, владеет разносторонними навыками и приемами решения предложенных заданий, а содержание работы изложено исчерпывающе полно, последовательно, четко и логически стройно, без каких-либо неточностей;
- оценка «хорошо» выставляется тогда, когда из работы ясно, что обучающийся твердо знает программный материал, правильно применяет теоретические положения при решении предложенных заданий, владеет необходимыми навыками и приемами их выполнения, а содержание работы изложено грамотно, без существенных неточностей;
- оценка «удовлетворительно» выставляется тогда, когда из работы ясно, что обучающийся имеет знания основного программного материала, но не усвоил его деталей, испытывает затруднения при решении предложенных заданий, в работе допущены неточности, недостаточно правильные формулировки, нарушения логической последовательности в изложении;
- оценка «неудовлетворительно» выставляется тогда, когда из работы ясно, что обучающийся не знает значительной части программного материала, неуверенно и с большими затруднениями выполняет работы, а в изложении работы допущены существенные ошибки.
Самостоятельная работа №1
Тема: Вычисление определителей матрицы
Цель: закрепление умения вычислять, миноры, алгебраические дополнения и определители четвертого порядка разложением по элементам строки (столбца).
Время выполнения: 6 часов (для 09.02.03, 09.02.04), 8 часов для (09.02.01)
Теоретический материал
Квадратной матрице А порядка n можно сопоставить число det A (или 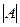 , или
, или 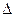 ), называемое её определителем, следующим образом:
), называемое её определителем, следующим образом:
1. если 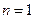 , то
, то 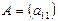 и
и 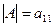 ;
;
2. если 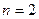 , то
, то 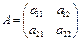 и
и 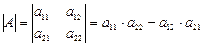 ;
;
3. если 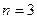 , то
, то 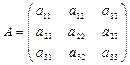 и
и
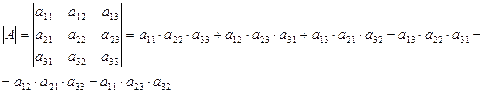
Определитель матрицы А также называют её детерминантом.
Вычисление определителя 2-го порядка иллюстрируется схемой:
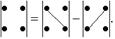
Рис.1. Схема вычисления определителя 2-го порядка.
Пример 1.Найти определители матриц: 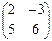 и
и 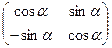 .
.
Решение: 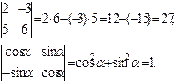
При вычислении определителя 3-го порядка удобно пользоваться правилом треугольников (или Саррюса),которое схематически можно записать так:
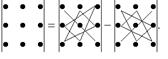
Рис.2. Схема вычисления определителя 3-го порядка (или Саррюса).
Пример 2.Вычислить определитель матрицы
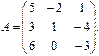
Решение:
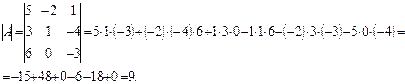
Для вычисления определителей более высоких порядков используются понятия минора и алгебраического дополнения.
Минором некоторого элемента 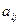 определителя n-го порядка называется определитель (n – 1)-го порядка, полученный из данного путём вычёркивания строки и столбца, на пересечении которых находится выбранный элемент. Минор каждого элемента обозначается символом
определителя n-го порядка называется определитель (n – 1)-го порядка, полученный из данного путём вычёркивания строки и столбца, на пересечении которых находится выбранный элемент. Минор каждого элемента обозначается символом 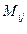
Так, если 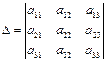 , то
, то 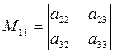 ,
, 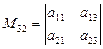 .
.
Алгебраическим дополнением элемента 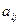 определителя называется его минор, умноженный на
определителя называется его минор, умноженный на 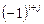 , т.е.
, т.е.
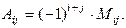 Так,
Так, 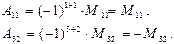
Теорема Лапласа. Определитель матрицы равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения.
Например, 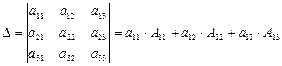
Данное свойство содержит в себе способ вычисления определителей высоких порядков.
Пример 3.Вычислите определитель 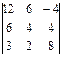 .
.
Решение:
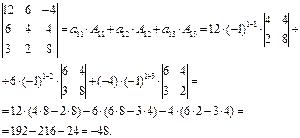
Задание для самостоятельной работы
Вычислить определители: 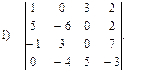
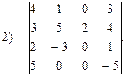
Рекомендуемая литература: 1.1[с.5], 1.2[с.7-10], 2.1[с.70-78].
Самостоятельная работа №2
Тема: Решение систем линейных уравнений различными методами
Цель: закрепление умений решения систем линейных уравнений по правилу Крамера, матричным методом и методом Гаусса.
Время выполнения: 6 часов.
Теоретический материал
Пусть дана система из n линейных уравнений с n неизвестными 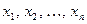
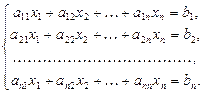 (1)
(1)
Числа 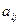 называются коэффициентами системы(1), а числа
называются коэффициентами системы(1), а числа 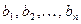 - свободными членами.
- свободными членами.
Система линейных уравнений называется однородной, если 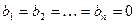 .
.
Матрица 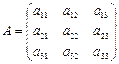 называется матрицей системы(1), а её определитель
называется матрицей системы(1), а её определитель 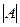 - определителем системы (1).
- определителем системы (1).
Решением системы(1) называется совокупность чисел, 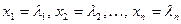 , которые обращают все уравнения системы в тождества.
, которые обращают все уравнения системы в тождества.
Система, у которой число неизвестных равно числу уравнений, называется совместной. В противном случае система называется несовместной.
Самостоятельная работа №3
Тема: Операции над векторами. Вычисление скалярного произведения через координаты векторов
Цель:закрепление умения производить действия над векторами в координатной и геометрической форме. Находить координаты вектора, модуль вектора, скалярное произведение векторов через координаты
Время выполнения: 4 часа
Теоретический материал
Вектором называется направленный отрезок. Обозначения: a, 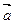 ,
, 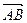
Векторы называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Вектор называется нулевым, если его начальная и конечная точки совпадают. Нулевой вектор не имеет определенного направления.
Два вектора называются равными, если они коллинеарны, имеют одинаковую длину (модуль) и одинаковое направление.
Проекциейвектора АВ на ось OX (OY) называется длина направленного отрезка А/В/ оси OX (OY), где А/ и В/ - основания перпендикуляров, опущенных из точек А и В на ось OX (OY).
Проекции вектора на координатные оси – координаты вектора: 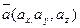 . Длина вектора находится по формуле
. Длина вектора находится по формуле
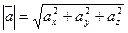 .
.
Пусть α, β, γ – углы, образованные вектором 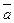 с осями координат (Ox, Oy, Oz соответственно), тогда
с осями координат (Ox, Oy, Oz соответственно), тогда
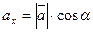 ,
, 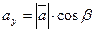 ,
, 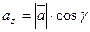
Самостоятельная работа №4
Тема: Кривые второго порядка
Цель: формирование умения составления уравнений кривых второго порядка.
Время выполнения: 6 часов.
Теоретический материал
Если Р(х; у) многочлен второй степени, то линии, определяемые уравнением.
Р(х; у)=0 (1),
называются линиями второго порядка, а уравнение (1) может быть записано в виде
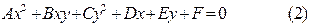
Линия второго порядка, задаваемая уравнением (2) в зависимости от коэффициентов А, В, С, D, Е, F, определяет эллипс, гиперболу или параболу, а при некоторых значениях коэффициентов - точку или две прямые (последние случаи называют вырожденными).
Окружностью радиуса R с центром в точке 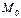 называется множество всех точек М плоскости, удовлетворяющих условию
называется множество всех точек М плоскости, удовлетворяющих условию 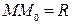 (см. рис.5).
(см. рис.5).
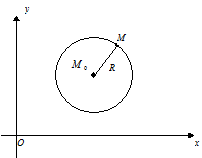
Рис. 5. Окружность со смещенным центром.
Каноническое уравнение окружности имеет вид:
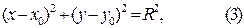
где х и у – текущие координаты, 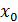 и
и 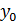 - координаты центра окружности, R – радиус окружности.
- координаты центра окружности, R – радиус окружности.
В частности, если 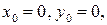 получим каноническое уравнение окружности с центром в начале координат
получим каноническое уравнение окружности с центром в начале координат 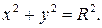
Как было сказано выше, окружность является линией второго порядка, следовательно, её уравнение тоже можно рассматривать как частный случай уравнения (2).
Если мы раскроем скобки в уравнении (3), то после некоторых преобразований мы получим уравнение вида
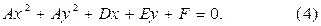
Мы видим, что уравнение (4) отличается от уравнения (2) только тем, что член, содержащий произведение ху, отсутствует.
Таким образом, окружность определяется общим уравнением второй степени с двумя переменными, если в нём коэффициенты при 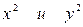 равны между собой и отсутствует член с произведением ху.
равны между собой и отсутствует член с произведением ху.
Эллипсом называется множество точек плоскости, декартовы координаты которых удовлетворяют уравнению:
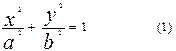
Числа а и b - полуоси эллипса.
Эллипс - это линия, симметричная относительно осей Ох и Оу.
Точки 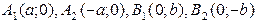 называются вершинами эллипса.
называются вершинами эллипса.
Из канонического уравнения эллипса мы можем вывести формулы для вычисления х и у:
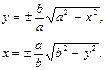
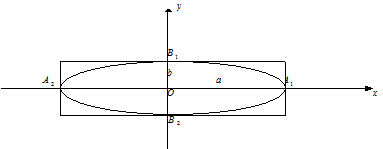
Рис. 6. Эллипс.
Гиперболой называется множество точек плоскости, декартовы координаты, которых удовлетворяют уравнению:
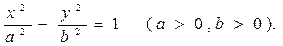
Из канонического уравнения гиперболы выводим уравнения х и у:
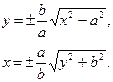
Гипербола состоит из двух частей, называемых ветвями.
При a=b гипербола называется равносторонней (равнобочной) и её уравнение имеет вид
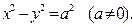
Гипербола, заданная уравнением вида 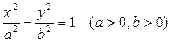 имеет вид:
имеет вид: 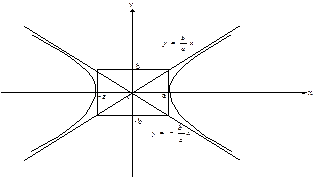
Рис.7. Гипербола.
Гипербола, заданная уравнением вида 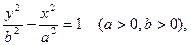 называется сопряжённой гиперболе
называется сопряжённой гиперболе 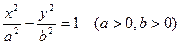 .
.
Центром гиперболы является начало координат. Точки пересечения гиперболы с осями симметрии называются вершинами гиперболы.
Числа a ,b –полуосями.
Прямые 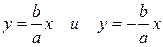 являются асимптотами гиперболы.
являются асимптотами гиперболы.
Задания для самостоятельной работы
Таблица 1
| Номер задачи | Текст задачи |
1. Составить уравнение гиперболы с фокусами на оси Ох, если расстояние между ее фокусами равно 20, а уравнение ее асимптот 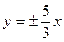 . 2. Составить уравнение директрисы параболы у2-4у-12х+16=0. . 2. Составить уравнение директрисы параболы у2-4у-12х+16=0. | |
| 1. Составить уравнение эллипса с фокусами на оси Ох, если расстояние между фокусами равно16, а эксцентриситет равен ½. 2. Составить уравнение оси параболы у2-6у-12х-15=0. | |
| 1. Составить уравнение эллипса с фокусами на оси Ох, если расстояние между фокусами равно12, а эксцентриситет равен 3/10. 2. Составить уравнение оси параболы у2+6у-8х+1=0. | |
1. Составить уравнение эллипса с фокусами на оси Ох, проходящего через точки А(6;4) и В( 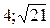 ). 2. Составить уравнение директрисы параболы у2+8у+28х+72=0. ). 2. Составить уравнение директрисы параболы у2+8у+28х+72=0. | |
1. Составить уравнение эллипса с фокусами на оси Ох, проходящего через точки ( 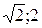 ) и ( ) и ( 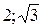 ). 2. Составить уравнение оси параболы у2-4у-16х+52=0. ). 2. Составить уравнение оси параболы у2-4у-16х+52=0. | |
1. Найти эксцентриситет эллипса 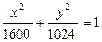 . 2. Составить уравнение оси параболы Х 2 +8х+16у+48=0. . 2. Составить уравнение оси параболы Х 2 +8х+16у+48=0. | |
1. Найти эксцентриситет гиперболы 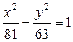 . 2. Составить уравнение директрисы параболы Х 2 +8х-28у+44=0. . 2. Составить уравнение директрисы параболы Х 2 +8х-28у+44=0. | |
1. Дан эллипс 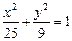 . Найти его полуоси и расстояние между фокусами. 2. Написать уравнение гиперболы, проходящей через точку (2;1) , асимптоты которой . Найти его полуоси и расстояние между фокусами. 2. Написать уравнение гиперболы, проходящей через точку (2;1) , асимптоты которой 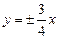 . . | |
1. Дана гипербола 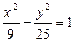 . Найти ее оси и расстояние между фокусами. 2. Написать уравнение параболы с вершиной в начале координат, если координаты фокуса равны F(0;-5). . Найти ее оси и расстояние между фокусами. 2. Написать уравнение параболы с вершиной в начале координат, если координаты фокуса равны F(0;-5). | |
| 1. Найти эксцентриситет эллипса 4х2+9у2=180. 2. Написать уравнение директрисы и найти координаты фокуса параболы У2=4х. |
Рекомендуемая литература: 1.1[с. 309-317], 1.2[с. 304-326], 2.1[с. 25-30].
Самостоятельная работа №5
Тема: Теория пределов
Цель: формирование умения доказывать основные положения и теоремы теории пределов.
Время выполнения:6 часов (для 09.02.03, 09.02.04), 10 часов для (09.02.01)
Теоретический материал
Пусть функция f(x) определена в некоторой окрестности точки х=а, кроме, может быть самой точки а.
Число А называется пределом функции f(x) при стремлении х к а (или в точке а), если для любого числа 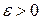 существует такое число
существует такое число 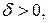 что для всех
что для всех 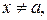 удовлетворяющих условию
удовлетворяющих условию 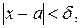 имеет место неравенство
имеет место неравенство 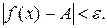
Обозначают: 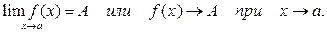
Из определения следует, что, если число А есть предел функции f(x) в точке х=а, то для всех х, достаточно близких к числу а и отличных от него соответствующие им значения функции f(x) оказываются сколь угодно близкими к числу А.
Число А называется пределом функции f(x) при стремлении х к бесконечности, если для любого числа 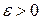 существует такое положительное число N, что для всех х удовлетворяющих условию
существует такое положительное число N, что для всех х удовлетворяющих условию 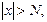 имеет место неравенство
имеет место неравенство 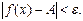
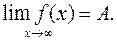
Бесконечно малая величина
Функция 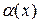 называется бесконечно малой при
называется бесконечно малой при 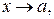 если
если 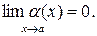
Бесконечно большая величина
Функция f(x) называется бесконечно большой при 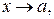 если
если 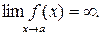
Основные теоремы о пределах
Теорема 1. Предел постоянной равен самой постоянной.
Теорема 2. Если функции f(x) u g(x)имеют пределы при 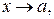 то при
то при 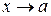 имеют пределы также их сумма f(x) + g(x), произведение
имеют пределы также их сумма f(x) + g(x), произведение 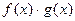 и при условии, что
и при условии, что
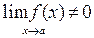 частное
частное 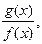 причём
причём
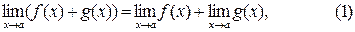
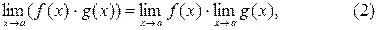
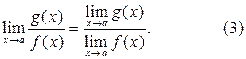
Следствие 1. Если функция f(x) имеет предел при 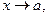 то
то
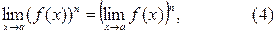 где n – натуральное число.
где n – натуральное число.
Следствие 2. Постоянный множитель можно выносить за знак предела:
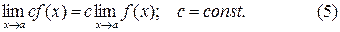
Задание для самостоятельной работы
Самостоятельная работа выполняется по вариантам. Каждый обучащийся вместо букв n и k ставит свои числа, где n – количество букв фамилии, k – количество букв полного имени. (Например: Иванов Федор – n=6, k=5)
Задание. Вычислить пределы
1. 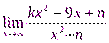 2.
2. 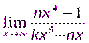 3.
3. 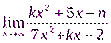 4.
4. 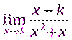
5. 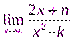 6.
6. 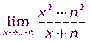 7.
7. 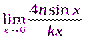 8.
8. 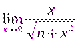
9. 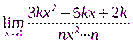
Рекомендуемая литература: 1.1[с. 193-208], 1.2[с. 71-87], 2.1[с.142-149].
Самостоятельная работа №6
Тема: Дифференциальное исчисление функции одной действительной переменной.
Цель: закрепление и систематизация знаний по теме «Производная и дифференциал функции».
Время выполнения: 6 часов (для 09.02.03, 09.02.04),10 часов для (09.02.01)
Теоретический материал
Пусть функция y=f(x) определена в промежутке (a;b). Возьмём какое-нибудь значение х из (a;b). Затем возьмём новое значение аргумента 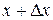 из этого промежутка, придав первоначальному значению х приращение
из этого промежутка, придав первоначальному значению х приращение 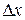 (положительное или отрицательное).
(положительное или отрицательное).
Этому новому значению аргумента соответствует и новое значение функции
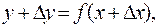 где
где 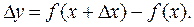
Теперь составим отношение
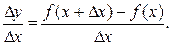 Оно является функцией от
Оно является функцией от 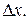
Если существует предел отношения 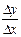 приращения функции
приращения функции 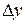 к вызвавшему его приращению аргумента
к вызвавшему его приращению аргумента 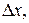 когда
когда 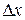 стремится к нулю, то этот предел называется производной от функции y=f(x) в данной точке х и обозначается через y’ или f’(x) (читается «игрек штрих» или «эф штрих от икс»):
стремится к нулю, то этот предел называется производной от функции y=f(x) в данной точке х и обозначается через y’ или f’(x) (читается «игрек штрих» или «эф штрих от икс»):
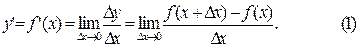
Для обозначения производной принят также и следующий символ 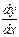 (читается «дэ игрек по дэ икс»). Эту запись надо рассматривать пока как целый символ, а не как частное.
(читается «дэ игрек по дэ икс»). Эту запись надо рассматривать пока как целый символ, а не как частное.
Действие нахождение производной называется дифференцированием, а функцию, имеющую производную в точке х, называют дифференцируемой в этой точке.
Функция, дифференцируемая в каждой точке промежутка, называется дифференцируемой в этом промежутке.
Задание для самостоятельной работы
Подготовить презентацию или сообщение на тему:
1) Задачи, приводящие к понятию производной.
2) Производная, ее геометрический и механический смысл.
Рекомендуемая литература: 1.1[с. 250-254], 1.2[с.180-184].
Самостоятельная работа №7
Тема: Вычисление собственных и несобственных интегралов
Цель: формирование умения вычислять несобственные интегралы с помощью формулы Ньютона-Лейбница.
Время выполнения: 5 часов (для 09.02.03, 09.02.04), 6 часов для (09.02.01)
Теоретический материал
При рассмотрении определённых интегралов мы предполагали, что область интегрирования ограничена (более конкретно, является отрезком [a,b]); для существования определённого интеграла 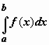 необходима ограниченность подынтегральной функции на [a,b].
необходима ограниченность подынтегральной функции на [a,b].
Будем называть определённые интегралы, для которых выполняются оба эти условия собственными; интегралы, для которых нарушаются эти требования (т.е. неограниченна либо подынтегральная функция, либо область интегрирования, либо и то, и другое вместе) несобственными.
Пример 1.
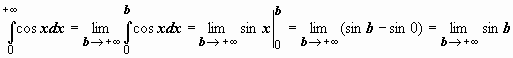 ;
;
этот предел не существует; следовательно, исследуемый интеграл расходится.
Пример 2. 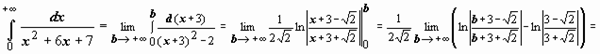
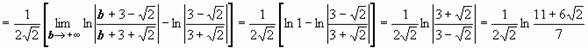 ; следовательно, интеграл сходится и равен
; следовательно, интеграл сходится и равен 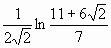 .
.
Аналогично интегралу с бесконечным верхним пределом интегрирования определяется интеграл в пределах от 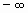 до b :
до b : 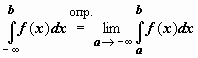 и в пределах от
и в пределах от 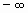 до
до 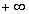 :
: 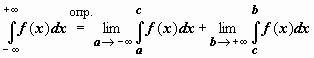 . В последнем случае f(x) определена на всей числовой оси, интегрируема по любому отрезку; c - произвольная (собственная) точка числовой оси; интеграл называется сходящимся, если существуют и конечны оба входящих в определение предела. Существование конечных пределов и их сумма не зависят от выбора точки c.
. В последнем случае f(x) определена на всей числовой оси, интегрируема по любому отрезку; c - произвольная (собственная) точка числовой оси; интеграл называется сходящимся, если существуют и конечны оба входящих в определение предела. Существование конечных пределов и их сумма не зависят от выбора точки c.
Пример 3.
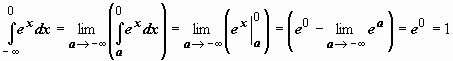 . Интеграл сходится.
. Интеграл сходится.
Пример 4. 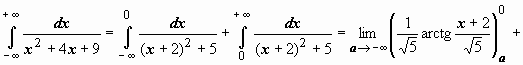
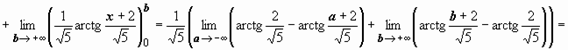
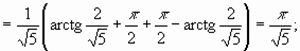 следовательно, интеграл сходится и равен
следовательно, интеграл сходится и равен 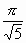 .
.
Формула Ньютона-Лейбница для несобственного интеграла.
Символом 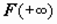 будем обозначать
будем обозначать 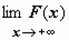 ; символом
; символом 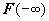 - соответственно,
- соответственно, 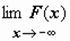 ; тогда можно записать
; тогда можно записать
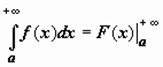 ,
, 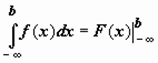 ,
, 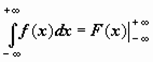 ,
,
подразумевая в каждом из этих случаев существование и конечность соответствующих пределов.
Теперь решения примеров выглядят более просто: 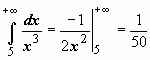 - интеграл сходится;
- интеграл сходится; 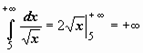 - интеграл расходится.
- интеграл расходится.
Для несобственных интегралов применимы формулы интегрирования по частям и замены переменной:
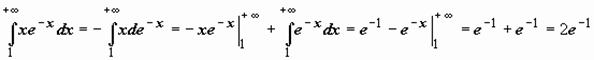
при замене переменной несобственный интеграл может преобразовываться в собственный.
Пример 6.
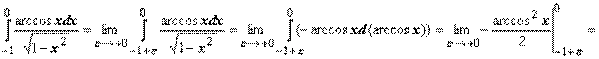
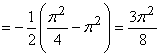 - интеграл сходится.
- интеграл сходится.
Применение формулы Ньютона-Лейбница.
Если для функции f(x) на полуинтервале (a, b] существует первообразная F(x), то
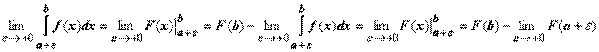 , и сходимость интеграла определяется наличием или отсутствием конечного предела
, и сходимость интеграла определяется наличием или отсутствием конечного предела 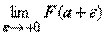 . Будем писать просто
. Будем писать просто 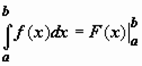 , имея в виду, что если соответствующий предел конечен, то интеграл сходится, в противном случае - расходится.
, имея в виду, что если соответствующий предел конечен, то интеграл сходится, в противном случае - расходится.
Пример 7. 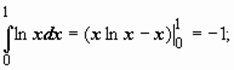 интеграл сходится.
интеграл сходится.
Пример 8. 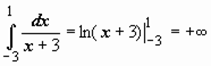 ; интеграл расходится.
; интеграл расходится.
Задание для самостоятельной работы
Вычислите несобственные интегралы:
1. 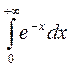 2.
2. 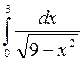 3.
3. 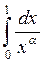 4.
4. 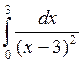 5.
5. 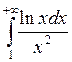
6. 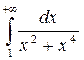 7.
7. 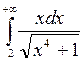 8.
8. 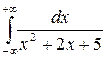
Рекомендуемая литература: 11.1[с. 271-282], 1.2[с. 205-212], 2.2<
