Оценка надежности по результатам испытаний

Подтверждение надежности при испытаниях типа «успех-отказ»

В общем случае отработку можно представить как процесс обнаружения неисправностей и их устранения. Он продолжается до тех пор, пока не будут удовлетворены требования, предъявляемые к надежности изделия. Расчетные соотношения для оценки надежности будут определяться особенностями функционирования объекта испытаний и возможностями измерительных средств. В одних случаях в процессе отработки фиксируется только факт отказа или успешного функционирования изделия, в других – в каждом испытании производят измерение целой группы параметров, характеризующих работоспособность изделия. При проведении испытаний по первой схеме (схеме «отказ-успех») в качестве точечной оценки надежности принимается вероятность безотказного функционирования изделия, рассчитываемая по соотношению

Ĥ = d / k,

где k – общее число испытаний, d – число безотказных испытаний.

Для иллюстрации в табл. 1.1 представлены статистические данные по результатам пусков зарубежных ракет-носителей. При ограниченных объемах испытаний эта оценка не даст гарантированный результат. В частности при проведении безотказных испытаний (k = d) точечная оценка будет равна 1 для всех k, в том числе и для k = 1. Очевидно, доверие к этой оценке мало. Поэтому для получения гарантированного результата необходимо переходить к интервальным оценкам. Согласно определению доверительного интервала, имеем

Р = { |Ĥ - Н| < ε } = γ

При подтверждении надежности нас, в основном, интересует вероятность того, что истинное значение надежности Н будет не ниже некоторого уровня Н_н, то есть

Р = { Н_н < Н} = γ

Это соотношение определяет одностороннюю нижнюю границу Н_н. Можно показать, что односторонняя нижняя граница Н_н является корнем уравнения

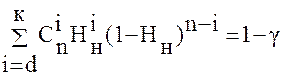
(3.1)

Для упрощения расчетов по соотношениям (3.1) были рассчитаны таблицы позволяющие по заданным значениям d, k и γ определять значения Н_н , являющиеся корнями уравнения (3.1). Фрагмент таблицы представлен ниже

Значения нижней границы доверительного интервала надежности для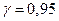

Число испытаний k	Число отказов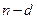
	0,55	0,34	0,19	0,08	0,01
	0,74	0,61	0,50	0,40	0,30	0,22
	0,82	0,72	0,64	0,56	0,49	0,42	0,40
	0,86	0,78	0,72	0,66	0,60	0,54	0,50	0,44

.

Аналитическое решение для Н_н удается получить только в случае безотказных испытаний. Тогда, полагая d = k , из соотношения (3.1) получим

Н^к = 1 – γ.

Отсюда

Н_Н = ^к√1 – γ. (3.2)

Эта формула находит широкое применение на практике при подтверждении работоспособности высоконадежных систем, так как в этом случае испытания, как правило, безотказные. Результаты расчета показывают, что для подтверждения высоких уровней надежности Н требуется очень большое число испытаний. Для примера ниже представлены объемы испытаний k и соответствующие им значения нижней границы Н_Н при безотказных испытаниях (γ = 0,95).

K				104
НН	0,74	0,97	0,997	0,9997

Очевидно, проведение большого количества испытаний для целого ряда уникальных дорогостоящих объектов не представляется возможным. Для указанных систем объем испытаний, как правило, предопределен возможностями технологической базы, стоимостью или сроками отработки. В связи с этим возникает задача подтверждения высоких уровней надежности при малом числе испытаний, рассматриваемая ниже.

Трудность статистического подтверждения высокого уровня надежности изделий при малом числе испытаний типа «успех – отказ» заключается в том, что в этом случае в процессе испытания используется минимальная информация о вероятностных свойствах изучаемого объекта и этот недостаток информации нужно компенсировать увеличением количества самих испытаний. В связи с этим возникает задача повышения информативности испытаний. В частности при измерении параметров, определяющих работоспособность устройства, объем испытаний может быть существенно сокращен. В этом случае для каждого из измеряемых параметров на основе анализа функционирования изделия можно определить области допустимых значений, соответствующие безотказной работе устройства. Тогда условие работоспособности будет определяться принадлежностью измеряемых параметров допустимой области.

В дальнейшем условие работоспособности по каждому из параметров представим в виде неравенства

η > 1

где η = х_доп / х_д – коэффициент запаса по рассматриваемому параметру;

х_д , х_доп – соответственно действующее и допустимое значение параметра.

Тогда вероятность отказа по данному параметру можно представить в виде

Q = Р{η < 1} (3.3)