Аналитическое дифференцирование

Операция дифференцирования реализована в Mathcad как в численной, так и в аналитической форме и обозначается при помощи традиционного оператора, т.е. соответствующими математическими символами (подобно сложению или умножению). ЕС помощью Mathcad можно вычислять производные скалярных функций любого количества аргументов, причем как функции, так и аргументы могут быть и действительными, и комплексными.

Для того чтобы аналитически найти производную функции f (х) в Mathcad:

1. Задайте функцию f (х).

2. Введите оператор дифференцирования нажатием кнопки Derivative (Производная) на панели Calculus (Вычисления) или введите с клавиатуры вопросительный знак <?>.

3. В появившихся местозаполнителях оператора дифференцирования введите функцию, зависящую от аргумента х, т.е. f(х), и имя самого аргумента х.

4. Введите оператор символьного вычисления для получения ответа.

Практическое задание!

Вычислите производные следующих функци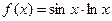й: ; . Для первой функции и ее производной постройте графики.

Численное дифференцирование

Для того чтобы численно продифференцировать функцию f (х) в некоторой точке, следует использовать оператор численного вывода (вместо символьного):

1. Определите точку х, в которой будет вычислена производная, например, х:=1.

2. Введите оператор дифференцирования и обычным образом введите имена функции и аргумента в местозаполнители.

3. Введите оператор = численного вывода результата.

Практическое задание!

Произведите численное дифференцирование функции 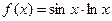в точках х=0,1; 0,5.

Производные высших порядков

Mathcad позволяет численно определять производные высших порядков, от 3-го до 5-го включительно. Чтобы вычислить производную функции f (х) N-го порядка, нужно проделать те же самые действия, что и при взятии первой производной, за тем исключением, что вместо оператора производной необходимо применить оператор м-й производной (Nth Derivative). Этот оператор вводится с той же панели Calculus (Вычисления), либо с клавиатуры нажатием клавиш <Ctrl>+<?>, и содержит еще два дополнительных местозаполнителя, в которые следует поместить число N.

Практическое задание!

Вычислите третью производную функции .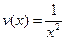

Интегрирование

Определенный интеграл

Интегрирование в Mathcad реализовано в виде вычислительного оператора. Допускается вычислять интегралы от скалярных функций в пределах интегрирования, которые также должны быть скалярными. Несмотря на то, что пределы интегрирования обязаны быть действительными, подынтегральная функция может иметь и комплексные значения, поэтому и значение интеграла может быть комплексным.

Интегрирование, как и дифференцирование, и множество других математических действий, устроено в Mathcad по принципу "как пишется, так и вводится". Чтобы вычислить определенный интеграл, следует напечатать его обычную математическую форму в документе. Делается это с помощью панели Calculus (Вычисления) нажатием кнопки со значком интеграла или вводом с клавиатуры сочетания клавиш <Shift>+<7> (или символа "&", что то же самое). Появится символ интеграла с несколькими местозаполнителями, в которые нужно ввести нижний и верхний интервалы интегрирования, подынтегральную функцию и переменную интегрирования.

Чтобы получить результат интегрирования, следует ввести знак равенства или символьного равенства. В первом случае интегрирование будет проведено численным методом, во втором — в случае успеха будет найдено точное значение интеграла с помощью символьного процессора Mathcad.

Можно вычислять интегралы с одним или обоими бесконечными пределами. Для этого на месте соответствующего предела введите символ бесконечности, воспользовавшись, например, той же самой панелью Calculus (Вычисления). Чтобы ввести (минус бесконечность), добавьте знак минус к символу бесконечности, как к обычному числу.

Подынтегральная функция может зависеть от любого количества переменных. Именно для того чтобы указать, по какой переменной Mathcad следует вычислять интеграл, и нужно вводить ее имя в соответствующий местозаполнитель. Помните, что для численного интегрирования по одной из переменных предварительно следует задать значение остальных переменных, от которых зависит подынтегральная функция и для которых вы намерены вычислить интеграл.

Практическое задание!

Вычислите определенный интеграл 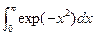. Вычислите для этой же функции интеграл от -¥ до +¥. Вычислите интеграл 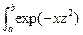по переменным х и z.

Неопределенный интеграл

Для того чтобы аналитически проинтегрировать некоторую функцию, следует ввести с панели Calculus (Вычисления) символ неопределенного интеграла, в появившемся в документе шаблоне заполнить местозаполнители и, наконец, ввести знак символьного равенства. В случае успеха по истечении некоторого времени расчетов справа от введенного выражения появится его аналитический результат. Если же функцию не удается проинтегрировать аналитически, введенное вами выражение будет просто продублировано.

Практическое задание!

Вычислите неопределенные интегралы: ;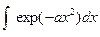

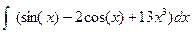
Содержание:

1 Основные сведения о MathCad. 2

2 Вычисления в MathCad. 4

2.1 Операторы численного и символьного ввода. Функции. 4

2.2 Переменные и оператор присваивания. 6

2.3 Функции. Графики функций. 7

2.3.1 Быстрое построение графика функции. Построение нескольких кривых в одной области. 7

2.3.2 Х-У график двух векторов. 8

2.3.3 Форматирование графиков. 9

2.3.4 Трехмерные графики. 11

3 Алгебраические вычисления. 11

3.1 Операторы.. 11

3.1.1 Арифметические операторы.. 11

3.1.2 Логические операторы.. 12

3.1.3 Матричные операторы.. 12

3.1.4 Операторы выражения. 13

3.2Алгебраические преобразования. 13

4 Дифференцирование. 15

4.1 Аналитическое дифференцирование. 15

4.2 Численное дифференцирование. 15

4.3 Производные высших порядков. 16

5 Интегрирование. 16

5.1 Определенный интеграл. 16

5.2 Неопределенный интеграл. 17