Описание линейной дискретной системы в Z – области

Математический аппарат z – преобразования, подобно преобразованию Лапласа в теории линейных аналоговых цепей, существенно упрощает анализ ЛДС.

Передаточная функция ЛДС

Применим z – преобразование к уравнению дискретной линейной свертки . В соответствии со свойствами z – преобразования получим:

, (3.1)

где - z – преобразования реакции и воздействия;

- z – преобразование импульсной характеристики.

Функция, представляющая собой z – преобразование импульсной характеристики

(3.2)

называется передаточной функцией (системной функцией) ЛДС.

Передаточная функция также может быть представлена и следующим образом:

. (3.3)

При известном изображении импульсная характеристика находится с помощью обратного z – преобразования:

. (3.4)

Таким образом, передаточная ЛДС – это отношение z – преобразования реакции к z – преобразованию воздействия.

Связь передаточной функции с разностным уравнением

Применим z – преобразование к разностному уравнению

.

В этом случае, учитывая свойство z – преобразования по запаздыванию воздействия, можно получить передаточную функцию ЛДС общего вида:

. (3.5)

Таким образом, передаточная функция ЛДС представляет собой дробно-рациональную функцию, числитель и знаменатель которой дееются многочленами аргумента порядков и с вещественными коэффициентами.

Как любая дробно-рациональная функция, передаточная функция ЛДС характеризуется полюсами и нулями.

Нулями называют значения , при которых передаточная функция равна нулю.

Полюсами называют значения , при которых знаменатель передаточной функции равен нулю.

Разновидности передаточных функций

Кроме передаточной функции общего вида, существуют другие формы записи передаточной функции.

Одна из эквивалентных форм записи передаточной функции выглядит следующим образом

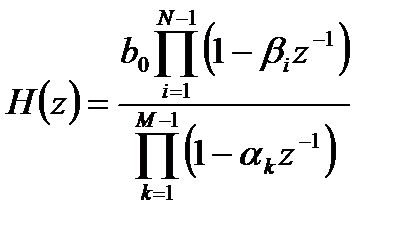, (3.6)

где 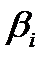- нули, 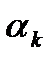- полюса.

Нули и полюса передаточной функции могут быть либо вещественными, либо составлять комплексно-сопряженные пары. Коэффициент усиления всегда вещественный.

Возможен третий вариант представления передаточной функции в виде суммы простых дробей ( :

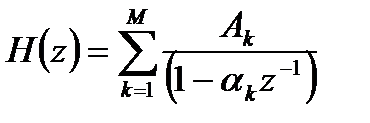, (3.7)

где 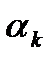- полюс;

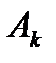- коэффициент разложения при k-м полюсе.

Оценка устойчивости ЛДС по ее передаточной функции

Представление функции передачи в виде суммы простых дробей позволяет найти импульсную характеристику системы через обратное z – преобразование, так как каждому слагаемому выражения (3.7) соответствует обратное преобразование вида :

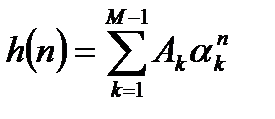. (3.8)

Таким образом, ряд будет сходиться и ЛДС будет устойчива, если выполняется условие:

(3.9)

Таким образом, для того, чтобы ЛДС была устойчива, необходимо и достаточно, чтобы все полюса ее передаточной функции распределялись внутри единичного круга комплексной z-плоскости.