Оптимальное управление линейной дискретной системой при аддитивных возмущениях и квадратичном критерии оптимальности

Рассмотрим задачу синтеза оптимального управления при коррекции движения ЛА. Процесс коррекции опишем линей­ным дискретным стохастическим уравнением с аддитивным возму­щением

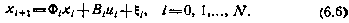
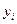В отличие от случая управления при полной информации будем считать, что измерению доступен не сам вектор состояния , а не­который вектор , связанный с соотношением

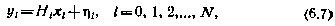
где через 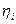обозначена случайная ошибка i-го измерения. В каче­стве критерия оптимальности по-прежнему принимаем критерий

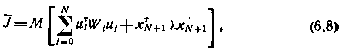
где 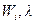— заданные матрицы.

Будем считать, что 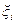, 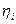— независимые гауссовские случайные векторы с характеристиками

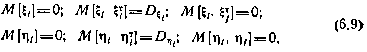
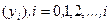Определим сначала достаточные координаты в данной задаче. В главе 3 показано, что апостериорная плотность вероятностей вектора по измерениям имеет вид

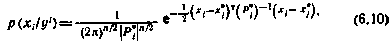
Там же показано, что вектор 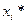и матрица 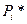определяемые в соответствии с (3.42), (3.43), являются соответственно апостериор­ным математическим ожиданием и апостериорной корреляционной матрицей вектора при заданных измерениях. Вектор 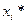дает оптимальную в смысле байесовского риска оценку вектора по всем прошлым и настоящим измерениям, матрица 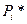характери­зует апостериорные среднеквадратичные отклонения ошибок этой оценки.

Из соотношений (3.42), (3.43) следует, что корреляционная матрица 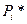не зависит от конкретных измерений и управлений. Она полностью определяется свойствами системы и канала наблю­дения (через матрицы 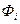, 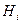), а также статистическими характе­ристиками 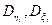возмущений 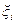и ошибок измерений 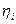и может быть определена заранее. Имея это в виду, можно считать, что плотность вероятностей 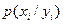в любой момент i полностью опре­деляется вектором 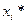и может быть представлена в виде 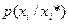. С другой стороны, знание 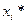согласно (3.42), (3.43) достаточно и для определения собственной будущей эволюции. Иными словами, вектор 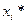является вектором достаточных координат в данной за­даче.

Теперь можно перейти к определению алгоритма оптимального управления. С этой целью преобразуем соотношение для вектора 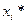. Представим соотношение (3.43) в следующем виде:

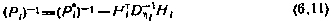
и подставим его в уравнение для 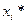. Учитывая также (3.42), по­лучим

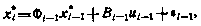
где

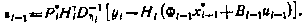
Последнее соотношение может быть приведено также к виду

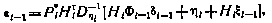
где .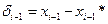

Это соотношение позволяет определить статистические свойства век­тора gj-i. В частности, нетрудно установить, что

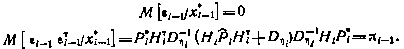
Итак, эволюция вектора достаточных координат может быть опи­сана уравнением

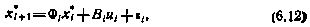
причем

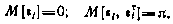
Воспользуемся рекуррентным соотношением (5.7). Примени­тельно к данной задаче оно принимает вид

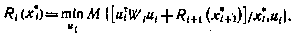
Это соотношение с точностью до обозначений совпадает с анало­гичным соотношением для случая управления линейной системой при полной информации. Поэтому совершенно аналогично можно получить следующее выражение для функции будущих потерь:

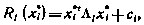
где

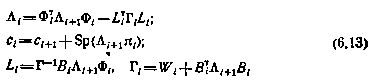
и для закона оптимального управления

Граничное условие для рекуррентных соотношений (6.13) полу­чим, рассмотрев последний шаг управления. Так как

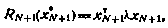
то, принимая во внимание связь

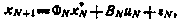
где

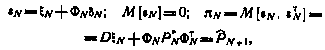
из основного рекуррентного соотношения находим

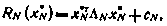
причем здесь

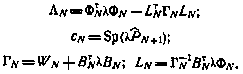
Сравнивая полученные соотношения с соотношениями (6.13), за­ключаем, что последние могут быть представлены более компакт­но в виде

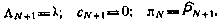
Ранее в гл. 5 было показано, что при аддитивных возмущениях алгоритм оптимального (в смысле квадратичного критерия) управ­ления при полной информации о линейной системе совпадает с алгоритмом оптимального управления соответствующей детерми­нированной системой. Полученное теперь решение формально так­же совпадает с детерминированным. Разница заключается лишь в том, что в алгоритме управления (6.14) вместо вектора фазовых координат выступает вектор достаточных координат 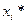(век­тор оптимальной оценки), определяемый в свою очередь с помо­щью фильтра Калмана.

Таким образом, в линейных системах с квадратичным критери­ем оптимальности при аддитивных гауссовских возмущениях оптимальный стохастический регулятор представляет собой после­довательное соединение фильтра Калмана для получения вектора достаточных координат (оптимальной оценки) и устройства опти­мального детерминированного управления. Сформулированный результат, известный в литературе также под названием теоремы разделения, находит широкое применение при получении прибли­женного решения нелинейных задач, когда задачу синтеза опти­мального управления при неполной информации разбивают на две — задачу определения оптимальных оценок вектора фазовых координат и задачу определения оптимального управления по пол­ным данным, решаемые независимо друг от друга (по аналогии с линейным случаем). Основанием для этого служит тот факт, что при формировании блока оптимальной оценки добиваются хорошей сходимости оценки к истинному вектору фазовых координат.