ЛДС с конечной и бесконечной импульсной характеристикой

Определим особенности импульсных характеристик рекурсивных и нерекурсивных ЛДС.

Учтем, что импульсная характеристика – это реакция на единичный дискретный импульс.

В результате замены в разностном уравнении входного сигнала на единичный дискретный импульс 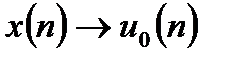, получим выражение для импульсной характеристики нерекурсивной ЛДС:

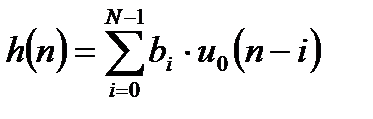
или в соответствии с определением единичного дискретного импульса

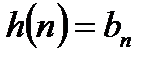. (2.1)

Соответственно, передаточная функция ЛДС с конечной импульсной характеристикой имеет следующий вид:

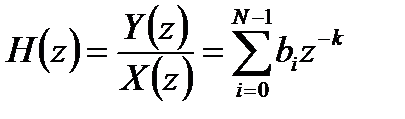. (2.2)

Таким образом, можно сделать следующие выводы:

- импульсная характеристика нерекурсивной ЛДС имеет конечную длительность, а значения отсчетов импульсной характеристики равны коэффициентам 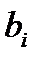разностного уравнения;

- нерекурсивные ЛДС называют системами с конечной импульсной характеристикой (КИХ, finite impulse response – FIR);

- передаточная характеристика нерекурсивной ЛДС не имеет полюсов;

- вследствие отсутствия обратных связей и полюсов передаточной функции любой нерекурсивный фильтр является устойчивым.

Простота анализа и реализации, абсолютная устойчивость нерекурсивных ЛДС привели к их широкому использованию на практике. Достоинством нерекурсивных ЛДС является возможность получения линейных фазочастотных характеристик. Однако для получения частотных характеристик с высокой прямоугольностью АЧХ необходимы фильтры высокого порядка – до нескольких сотен и даже тысяч.

Импульсная характеристика рекурсивного фильтра рассчитывается значительно сложнее. Ранее было аналитически получено, что импульсная характеристика рекурсивного фильтра с полюсами в передаточной функции описывается бесконечными степенными рядами:

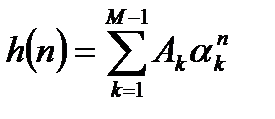. (2.3)

где 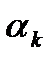- полюс;

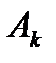- коэффициент разложения при k-м полюсе.

Передаточная функция рекурсивной ЛДС описывается передаточной дееюей ЛДС общего вида:

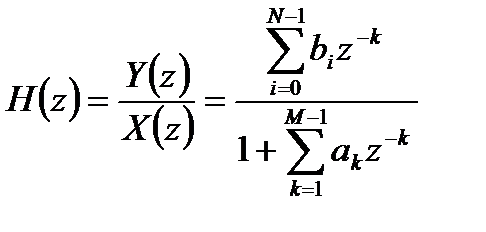, (2.4)

и ее эквивалентными формами записи через произведение сомножителей и в виде суммы простых дробей:

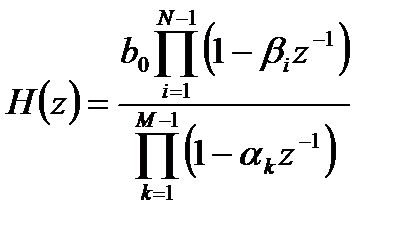, (2.5)

где 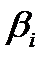- нули, 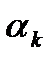- полюса;

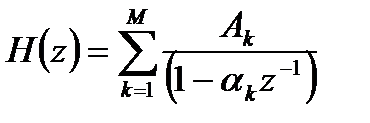, (2.6)

где 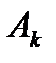- коэффициент разложения при k-м полюсе.

Таким образом, можно сделать следующие выводы:

- наличие в схеме расчетов рекурсивного фильтра обратных связей позволяет получить бесконечную импульсную характеристику;

- рекурсивные фильтры также называются фильтрами с бесконечной импульсной характеристикой (БИХ, infinite impulse response – IIR);

- передаточная функция рекурсивных фильтров всегда имеет полюса;

- из-за наличия обратных связей и полюсов передаточной функции рекурсивные фильтры могут быть неустойчивыми.

Достоинством рекурсивных фильтров является высокая крутизна спадов АЧХ даже при малом порядке фильтра. Недостатком рекурсивных фильтров является нелинейность фазочастотной характеристики.

Структурные схемы ЛДС

ЛДС может быть реализована аппаратным или программным способами. В первом случае используются микросхемы в виде регистров, умножителей, сумматоров. Во втором случае составляется программа расчета с указанием, какие операции и в какой последовательности необходимо выполнить, причем элемент задержки соответствует ячейке памяти для хранения отсчетов.

По одному уравнению при аппаратной реализации можно разработать ЛДС с различным числом регистров и сумматоров, а значит с различным временем обработки, габаритными размерами и ценой.

При программной реализации ЛДС различия в структурных схемах приводят к различиям в быстродействии и ошибках, обусловленных конечной разрядностью.

Следовательно, выбор оптимальной структуры ЛДС является актуальной задачей.

Утверждается, что для ЛДС второго порядка существует около 100 вариантов структурных схем.

Сложность реализации некоторых вариантов структурных схем ЛДС отображена в Таблице 3.1.

Таблица 3.1. Сложность структурной реализации ЛДС

	Прямая форма	Обращенная форма	Каноническая форма 1	Каноническая Форма 2
Элементы задержки	2N	2N	N	N
Число умножений	2N+1	2N+1	2N+1	2N+1
Сумматоры		2N		N+1
Число точек распределения сигналов	2N		N+1

Рассмотрим наиболее распространенные варианты структурных схем ЛДС.

3.2.3.1. Прямая и обращенная структуры ЛДС

Прямая структура основана на представлении передаточной функции ЛДС в общем виде:

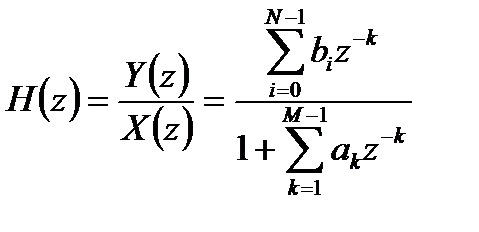. (3.1)

Такой передаточной функции соответствует разностное уравнение вида:

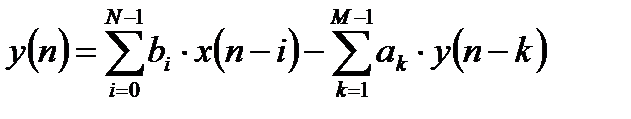. (3.2)

Прямая структура ЛДС 2-го порядка, соответствующая записанным передаточной функции общего вида и разностному уравнению, имеет вид, приведенный на рисунке 3.1.

Рисунок 3.1а – прямая структура рекурсивного фильтра 2-го порядка

Выходом ЛДС с прямой структурой является выход сумматора. В прямой форме структурной схемы четко выделены нерекурсивная и рекурсивная части. В прямой структуре ЛДС в линиях задержки хранятся непосредственно отсчеты входного и выходного сигналов и повышенная разрядность линий задержки не требуется. Однако в прямой структуре необходим сумматор повышенной разрядности.

Обращенная структура

Обращенная структура соответствует последовательному включению рекурсивной и нерекурсивной части. Один из вариантов обращенных структур (рисунок 3.1б) описывается следующими уравнениями и характеризуется использованием простых двухвходовых сумматоров:

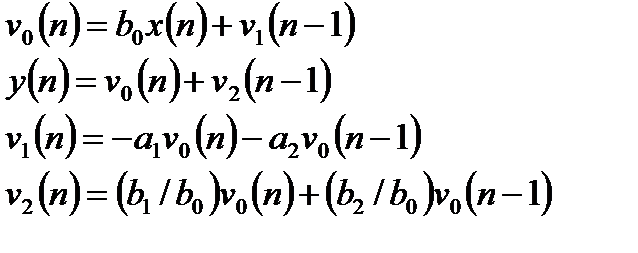. (3.2б)

Рисунок 3.1б – обращенная структура рекурсивного фильтра 2-го порядка

3.2.3.2. Канонические структуры ЛДС

Структуру ЛДС называют канонической, если число элементов задержки минимально и равно порядку передаточной функции.

Известно более 30 канонических структур ЛДС второго порядка, среди которых практическое применение нашли 2 структуры, характеризуемые минимальным количеством умножителей.

Каноническая структура 1

Эта структура основана на эквивалентном представлении передаточной функции в виде произведения:

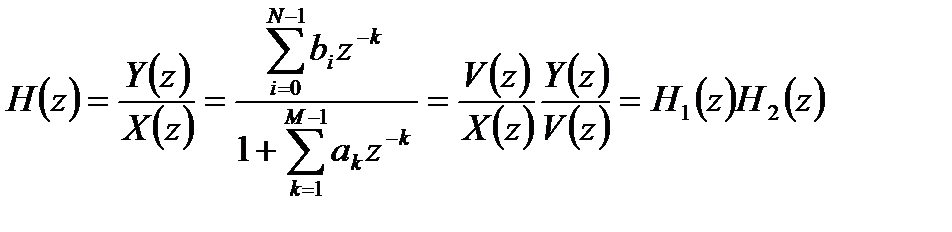, (3.3)

где ;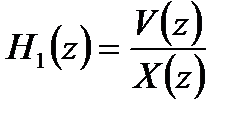

.

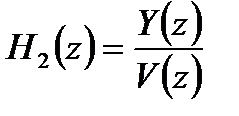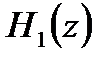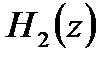Передаточным функциям и соответствуют разностные уравнения:

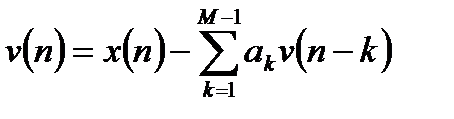, (3.4)

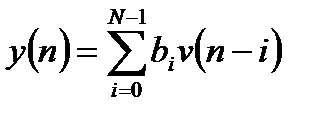, (3.5)

отображаемые прямыми структурами. В частности, на рисунке 3.2 показаны данные прямые структуры для ЛДС 2-ого порядка:

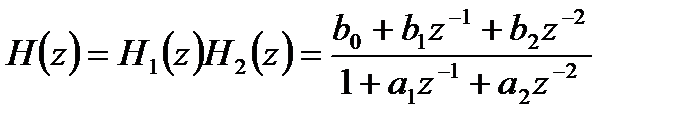, (3.6)

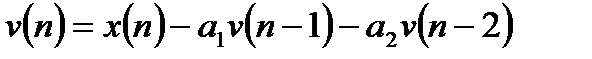, (3.7)

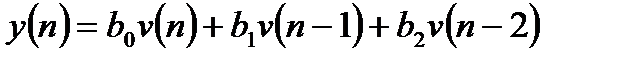. (3.8)

Объединение двух линий задержки в одну приводит к канонической структуре 1.

При канонической прямой реализации 1 используется общая линия задержки, что уменьшает число необходимых ячеек памяти. Однако при этом абсолютные величины отсчетов сигналов в линиях задержки могут существенно превосходить амплитуду входного и выходного сигналов, что требует увеличения разрядности представления чисел в линиях задержки.

Полезным свойством канонической структуры 1 является его соответствие представлению ЛДС в пространстве состояний. При этом вектор состояния представляет собой набор значений выходов элементов задержки.

Рисунок 3.2 – каноническая структура 1 рекурсивной ЛДС 2-го порядка

Каноническая структура 2

Эта структура основана еще на одном эквивалентном представлении передаточной функции общего вида в предположении 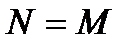. Умножая обе части передаточной функции 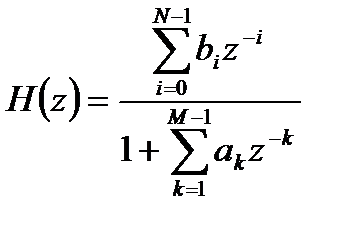на 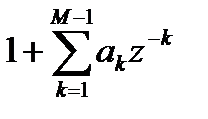, получим:

.

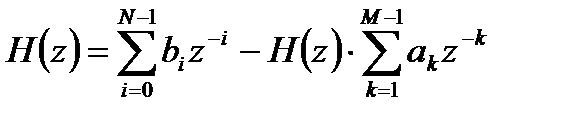Соответственно, вычисление передаточной функции может быть представлено в виде системы уравнений, где каждое последующее уравнение зависит от предыдущего:

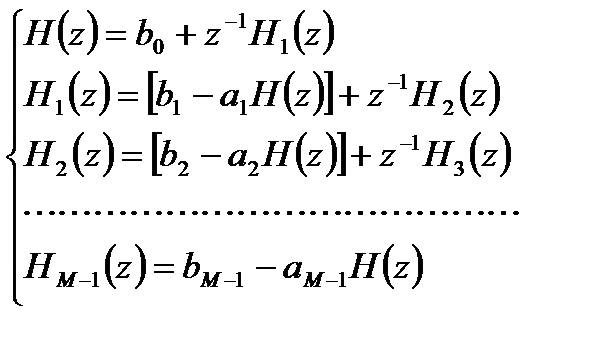. (3.17)

Для записи системы разностных уравнений умножим правую и левую части уравнений (3.17) на :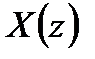

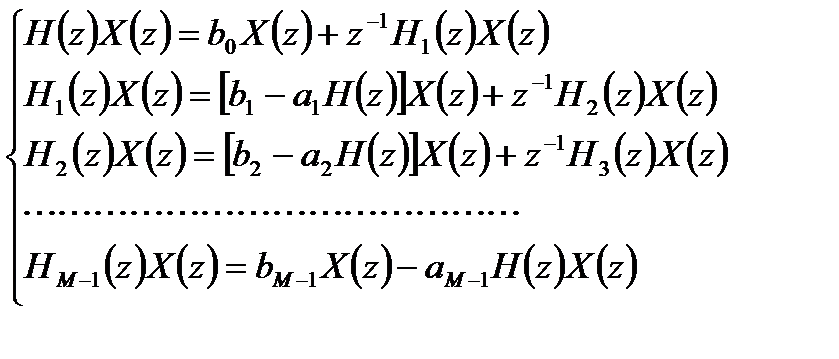. (3.19)

Введем обозначения

.

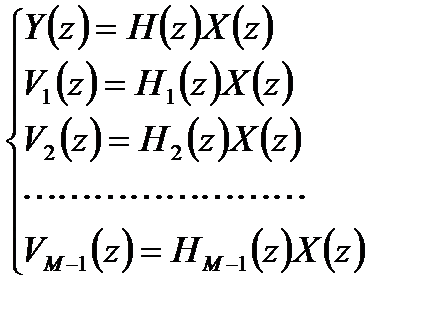В этом случае в результате обратного 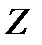- преобразования можно получить следующую систему разностных уравнений:

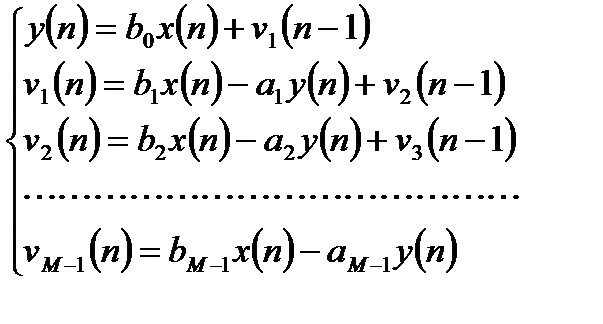. (3.20)

Последнее разностное уравнение соответствует прямой канонической структуре, которую удобно начинать с последнего уравнения системы и заканчивать первым уравнением системы.

Для звена 2-го порядка передаточные функции (3.17) примут вид:

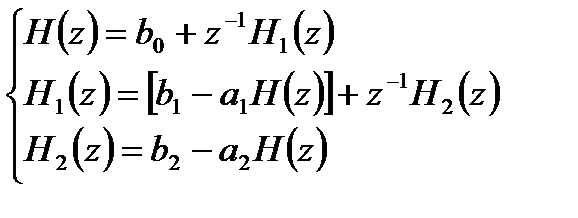. (3.21)

Соответственно, разностные уравнения запишутся следующим образом:

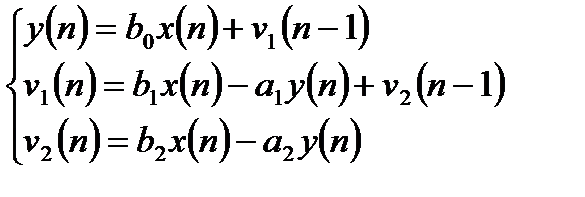. (3.22)

Структурная схема канонической структуры 2 для звена 2-го порядка приведена на рисунке 3.4. Каноническая структура 2 также называется транспонированной формой (direct transposed form II).

Транспонированная форма позволяет эффективно распараллелить вычисления и применяется в специализированных интегральных схемах. В такой схеме, как в любой прямой реализации, можно одновременно выполнять все операции умножения, однако дополнительно можно одновременно выполнять и все операции сложения, так как они являются независимыми. Для расчета выходного сигнала необходимо выполнить одно умножение и одно сложение. Остальные операции являются подготовительными.

Рисунок 3.4 – каноническая структура 2 рекурсивной ЛДС 2-го порядка

3.2.3.3. Последовательная (каскадная) и параллельная структуры ЛДС

ЛДС высокого порядка никогда не реализуются в прямой или канонической форме. Эффекты конечной разрядности при представлении коэффициентов значительно меньше влияют на характеристики ЛДС, если ее представить в виде последовательной или параллельной структуры, содержащей ЛДС второго порядка.

Последовательная (каскадная) форма ЛДС основана на представлении передаточной функции ЛДС ее эквивалентной формой записи через произведение простейших сомножителей второго порядка:

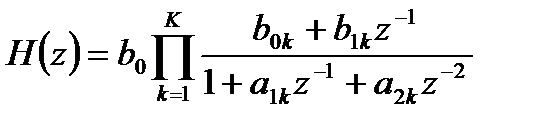, (3.23)

где 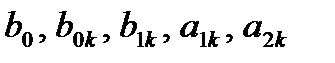- вещественные коэффициенты;

K – количество звеньев.

Параллельная форма ЛДС основана на представлении передаточной функции ЛДС ее эквивалентной формой записи в виде суммы простых дробей второй степени:

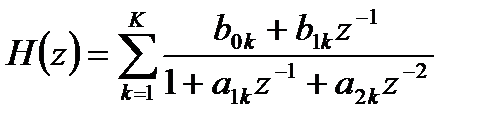, (3.24)

где 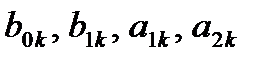- вещественные коэффициенты;

K – количество звеньев.

Коэффициенты 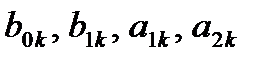могут быть получены в том числе методом неопределенных коэффициентов. В этом случае:

1) Правая часть последнего выражения приводится к общему знаменателю.

2) В числителе при этом образуется полином, который эквивалентен исходному полиному передаточной функции.

3) Требуемые коэффициенты полиномов числителей передаточных функций находятся путем решения системы уравнений из условия эквивалентности образованного полинома числителя и исходного полинома числителя:

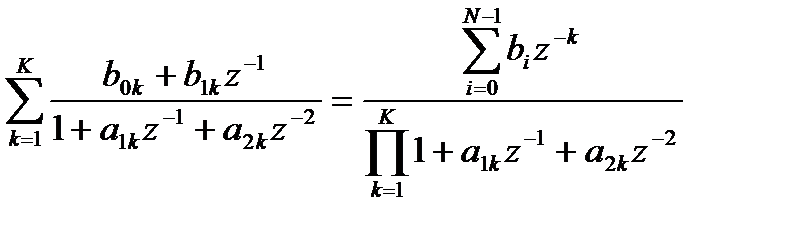. (3.25)