Методические указания к решению задач по статике

Плоская система сил

При решении задач на равновесие твердого тела, находящегося под действием плоской произвольной системы сил, применяются уравнения равновесия в одной из следующих форм [1]:

– суммы проекций на декартовы оси координат и сумма алгебраических моментов всех сил системы относительно произвольной точки плоскости действия сил равны нулю:

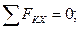
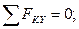
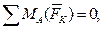
– сумма проекций на некоторую ось и сумма алгебраических моментов всех сил системы относительно двух точек плоскости, не принадлежащих прямой, перпендикулярной к оси проекций, равны нулю:

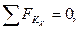
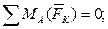
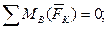
– суммы алгебраических моментов всех сил системы относительно трех точек плоскости действия сил, не принадлежащих одной прямой, равны нулю:

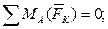
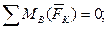
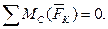
Проекция силы на ось (рис. 5) записывается по формуле:

.

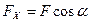Проекция будет положительна, если направлена в положительном направлении оси.

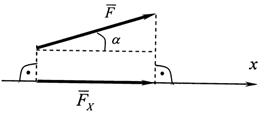
Рисунок 5 – Проекция силы

Алгебраическим моментом силы относительно данной точки называется взятое со знаком плюс или минус произведение модуля силы на ее плечо относительно этой точки (рис. 6), т.е., где h – плечо силы относительно точки А.

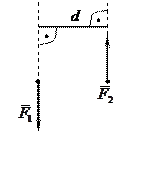
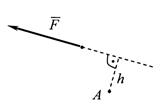
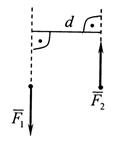
Рисунок 6 – Плечо силы Рисунок 7 – Пара сил

Момент считается положительным, если сила стремится вращать тело вокруг данной точки против часовой стрелки; если по часовой стрелке, то момент считается отрицательным.

Парой сил называется система двух равных по модулю, параллельных и противоположно направленных сил, приложенных к твердому телу (рис. 7). Алгебраический момент пары сил определяется по формуле

,

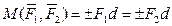где d – плечо пары сил (рис. 7).

Правило знаков для алгебраических моментов силы и пары сил одинаково.

С целью получения более простых уравнений суммы моментов сил рекомендуется составлять относительно точек, через которые проходят линии действия неизвестных сил.

В тех случаях, когда запись момента усложняется из-за трудностей при нахождении плеча силы, удобно разложить ее на составляющие, для которых плечи легко определяются, и воспользоваться теоремой Вариньона:

,

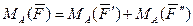где 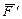, 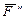– составляющие силы 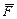, т.е. .

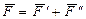План решения задач

1) Выделить на рисунке твердое тело, равновесие которого следует рассмотреть.

2) Изобразить векторы сил и моменты пар сил задаваемой нагрузки, приложенной к выделенному телу.

3) Выбрать систему координат.

4) Освободить тело от связей (опор) и заменить их соответствующими реакциями связей. Основные виды связей и их реакции приведены в любом учебнике по теоретической механике (раздел «Статика»), например в [1].

5) Для системы сил, приложенных к телу, составить уравнения равновесия.

6) Решив полученную систему уравнений, определить неизвестные реакции связей.

Пример 1. Балка АВ (рис. 8) находится в равновесии. Сила G=10 кН, момент пары сил М=8 кН*м, интенсивность распределенной нагрузки q=0,5 кН/м, Р=5 кН, ; размеры указаны в м.

Определить реакции неподвижного цилиндрического шарнира А и невесомого жесткого стержня СD.

Решение: Рассмотрим равновесие балки АВ (рис. 8).

Изобразим задаваемые силы, действующие на балку: сила 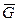, равнодействующая 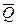равномерно-распределенной нагрузки, по величине равная 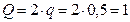кН и приложенная в середине участка действия этой нагрузки; пара сил с моментом М; сила 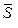натяжения троса, модуль которой равен P и которая направлена вдоль троса от балки.

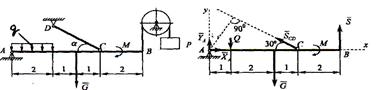
Рисунок 8 – К примеру 1 Рисунок 9 – К примеру 1

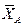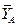Отбрасываем связи: шарнирно-неподвижную опору А и невесомый жесткий стержень CD. Действие связей заменяем их реакциями (рис. 9). Реакцию опоры А представляем двумя составляющими и . Силу реакции стержня 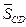направляем вдоль стержня от балки (можно ввести ее и в обратном направлении).

Для плоской произвольной системы сил, приложенных к балке, составляем три уравнения равновесия:

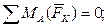
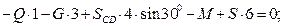
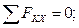
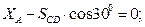
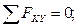
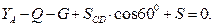
Решив систему уравнений, получим:

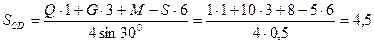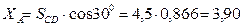кН.

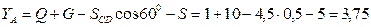кН.

кН.

Значения 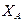, , 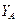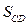получились положительными. Следовательно, принятые направления этих сил совпадают с их действительными направлениями.

Пример 2. Жесткая рама АВ (рис. 10) находится в равновесии. Интенсивность распределенной нагрузки q=1 кН/м, момент пары сил М=10 кН*м, Р=5 кН, 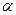=60⁰; размеры – в м. Определить реакции жесткой заделки А.

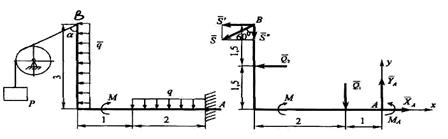Рисунок 10 – К примеру 2 Рисунок 11 – К примеру 2

Решение: Рассмотрим равновесие жесткой рамы АВ (рис. 10). Укажем задаваемые силы, действующие на раму. Такими силами будут являться равнодействующие равномерно распределенных нагрузок на горизонтальном и вертикальном участках рамы – силы 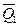и 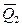, по модулю равные кН, 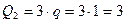кН и приложенные в серединах соответствующих участков; пара сил с моментом М; сила 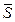натяжения троса, по модулю равная 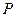и направленная вдоль троса от рамы. Отбрасываем связь – жесткую заделку в точке А. Действие жесткой заделки заменяем ее реакциями: двумя составляющим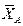и и 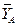силы и парой с моментом 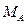. Для удобства составления уравнения моментов силу 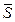раскладываем на составляющие 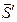и 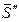(рис. 11), по величине равные:

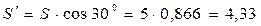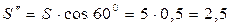кН,

кН.

Три уравнения равновесия будут иметь вид:

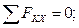
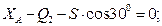
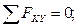
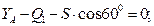
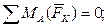
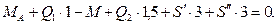
Из уравнений получаем:

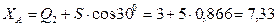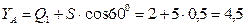кН;

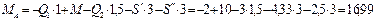кН;

кН.