Приближенные вычисления с помощью рядов тейлора
Ряды Тейлора и Маклорена широко применяются для приближенных вычислений значений функции 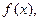 пределов, определенных интегралов, решений дифференциальных уравнений. Например, для вычисления значения
пределов, определенных интегралов, решений дифференциальных уравнений. Например, для вычисления значения 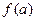 функцию
функцию 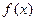 приближенно заменяют многочленом Тейлора
приближенно заменяют многочленом Тейлора 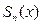 , а затем полагают
, а затем полагают 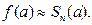
О п р е д е л е н и е 6. Функция 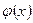 является в точке
является в точке 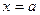 бесконечно малой функцией более высокого порядка, чем функция
бесконечно малой функцией более высокого порядка, чем функция 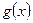 , если
, если
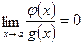 .
.
В этом случае пишут: 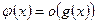 при
при 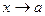 .
.
З а м е ч а н и е 6.Символ 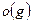 обозначает л ю б у ю функцию, бесконечно малую в точке
обозначает л ю б у ю функцию, бесконечно малую в точке 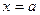 , имеющую более высокий порядок малости, чем
, имеющую более высокий порядок малости, чем 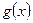 .
.
Справедливы с в о й с т в а:
1) 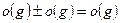 , 2)
, 2) 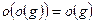 , 3)
, 3) 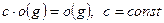 ,
,
4) 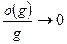 при
при 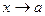 , 5)
, 5) 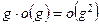 .
.
О п р е д е л е н и е 7.Если при 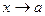 функция
функция 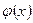 представима в виде суммы
представима в виде суммы 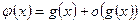 , где
, где 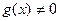 , то говорят, что функция
, то говорят, что функция 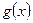 – главная часть функции
– главная часть функции 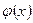 при
при 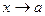 .
.
Основные разложения (11)-(23) позволяют легко выделять главные части многих функций. Например, при 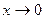 имеем:
имеем:
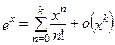 ,
, 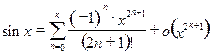 ,
,
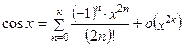 ,
, 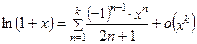 .
.
Знание главных частей функций часто используется при вычислении пределов.
ПРИМЕРЫ С РЕШЕНИЯМИ
П р и м е р 1. Для функции 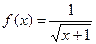 найти многочлен Тейлора
найти многочлен Тейлора 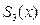 с центром в точке: а)
с центром в точке: а) 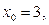 б)
б) 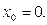
Р е ш е н и е. Функция 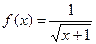 дифференцируема по
дифференцируема по  любое число раз на интервале
любое число раз на интервале  При этом имеем:
При этом имеем:
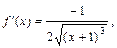
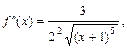
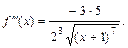
Следовательно, по формуле (7) получаем:
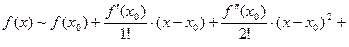 … .
… .
Поэтому многочлен Тейлора 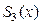 для рассматриваемой функции можно записать по формуле (1):
для рассматриваемой функции можно записать по формуле (1):
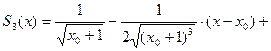
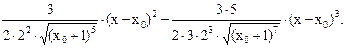
Таким образом, получаем:
а) при 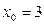
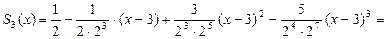
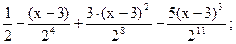
б) при 
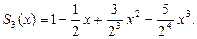
О т в е т: а) 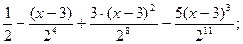 б)
б) 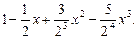
П р и м е р 2. Найти ряд Маклорена для функции 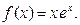
Р е ш е н и е. С п о с о б I. Функция 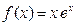 дифференцируема по
дифференцируема по 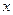 любое число раз на интервале
любое число раз на интервале  Вычисляем:
Вычисляем:
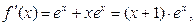
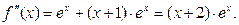
Проверим, что 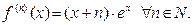 Предположив, что эта формула верна при некотором
Предположив, что эта формула верна при некотором 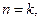 то есть
то есть 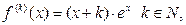 найдем
найдем 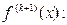
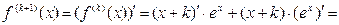
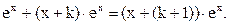
Следовательно, согласно методу математической индукции, формула 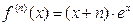 верна при любом натуральном
верна при любом натуральном  Поэтому получаем:
Поэтому получаем:
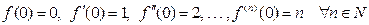 .
.
Следовательно, ряд Маклорена для функции 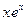 имеет вид:
имеет вид:
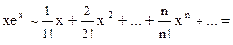
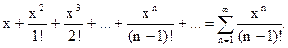
С п о с о б II. Так как 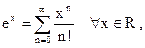 то
то
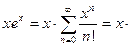
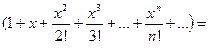
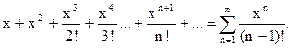
В этой формуле знак «=» между функцией 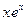 и ее рядом Маклорена поставлен на основании знака «=» в формуле (11) и свойств степенных рядов в их интервале сходимости.
и ее рядом Маклорена поставлен на основании знака «=» в формуле (11) и свойств степенных рядов в их интервале сходимости.
О т в е т: 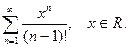
П р и м е р 3. Разложить функцию 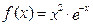 по степеням
по степеням 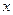 .
.
Р е ш е н и е. Из формулы (11) получаем заменой 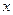 на
на 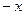 :
:
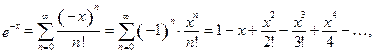
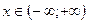 .
.
Поэтому получаем:
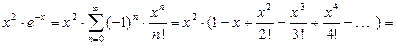
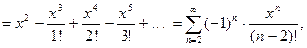
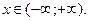
О т в е т: 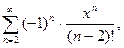
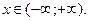
П р и м е р 4. Разложение в ряд Маклорена функцию 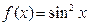 .
.
Р е ш е н и е. Так как 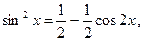 то, воспользовавшись формулой (16), находим:
то, воспользовавшись формулой (16), находим:
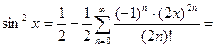
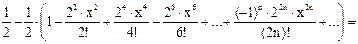
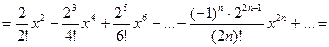
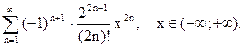
О т в е т: 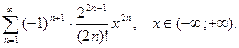
П р и м е р 5. Написать разложение функции 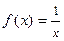 по степеням
по степеням 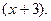
Р е ш е н и е. Обозначим: 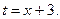 Тогда справедливо представление:
Тогда справедливо представление:
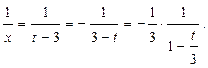 (24)
(24)
Воспользуемся рядом (18) для разложения функции 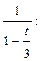
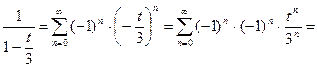
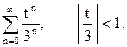
Следовательно, по формуле (24) находим:
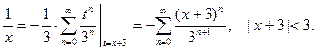
О т в е т: 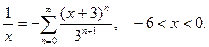
П р и м е р 6. Разложить функцию 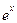 по степеням
по степеням 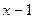 .
.
Р е ш е н и е. Пусть 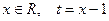 (значит,
(значит, 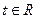 ). Тогда из основного разложения (11) получаем:
). Тогда из основного разложения (11) получаем:
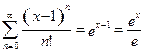 .
.
Отсюда находим:
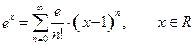 .
.
О т в е т: 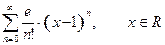 .
.
П р и м е р 7. Разложить функцию 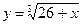 по степеням
по степеням 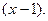
Р е ш е н и е. Обозначим: 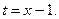 Тогда справедливо представление:
Тогда справедливо представление:
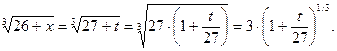
Поэтому с учетом формулы (17) при 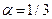 получаем:
получаем:
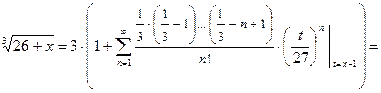
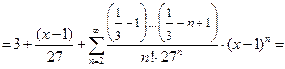
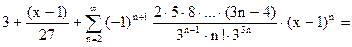
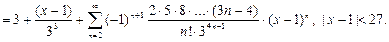
О т в е т: 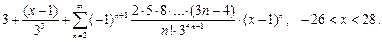
П р и м е р 8. Разложить функцию 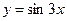 по степеням
по степеням 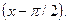
Р е ш е н и е. Обозначим: 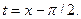 Тогда с учетом формул приведения справедливы равенства:
Тогда с учетом формул приведения справедливы равенства:
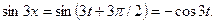
Поэтому, воспользовавшись разложением (16), получаем:
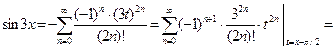
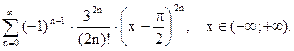
О т в е т: 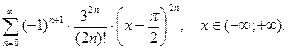
П р и м е р 9. Разложить функцию 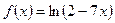 по степеням
по степеням 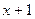 .
.
Р е ш е н и е. Обозначим: 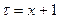 . Тогда
. Тогда 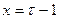 и справедливы равенства:
и справедливы равенства: 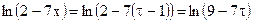
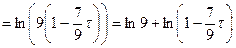 . Пусть
. Пусть
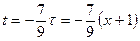 .
.
Тогда, воспользовавшись основным разложением (21), имеем:
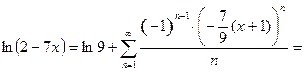
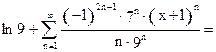
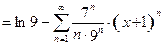 . (25)
. (25)
Так как ряд (21) сходится при 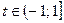 и
и 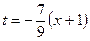 , то разложение (25) справедливо при
, то разложение (25) справедливо при 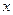 , удовлетворяющих неравенствам:
, удовлетворяющих неравенствам:
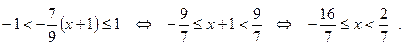
О т в е т: 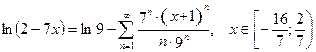 .
.
П р и м е р 10. Вычислить 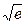 с точностью
с точностью 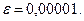
Р е ш е н и е. Воспользуемся разложением (11) функции 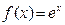 в ряд Маклорена. Тогда при
в ряд Маклорена. Тогда при 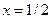 получаем:
получаем:
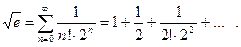 (26)
(26)
Подберем натуральное число 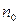 так, чтобы погрешность приближенного равенства
так, чтобы погрешность приближенного равенства
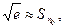 где
где 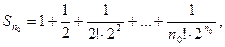
не превышала 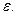 Для этого оценим остаточный член ряда (26):
Для этого оценим остаточный член ряда (26):
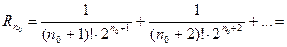
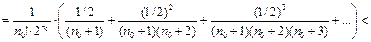
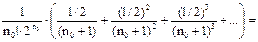
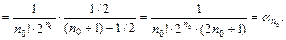
Следовательно, число 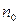 нужно подобрать таким, чтобы выполнялось неравенство:
нужно подобрать таким, чтобы выполнялось неравенство: 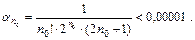 Пусть, например,
Пусть, например, 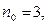 тогда
тогда
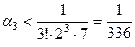 и
и 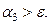
Аналогично проверяем: 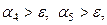 но
но 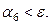 Следовательно, выбираем:
Следовательно, выбираем: 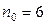 , при этом
, при этом 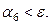 Тогда приближенно с точностью
Тогда приближенно с точностью 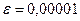 получаем:
получаем:
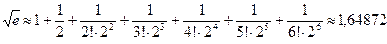 .
.
О т в е т: 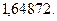
П р и м е р 11. Вычислить число 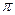 с точностью 0,01.
с точностью 0,01.
Р е ш е н и е. Воспользуемся рядом Маклорена для функции 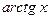 :
:
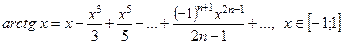 .
.
Пусть 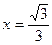 (
( 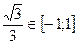 ). Тогда получаем:
). Тогда получаем:
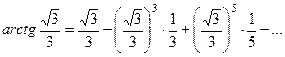 .
.
Напомним, что 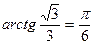 . Поэтому
. Поэтому
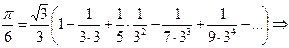
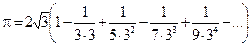 . (27)
. (27)
Обозначим:
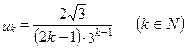 .
.
Тогда получим:
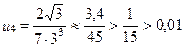 ,
, 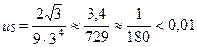 .
.
Следовательно, учитывая, что в (27) фигурирует знакочередующийся ряд и погрешность приближенного равенства 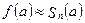 не превосходит по модулю числа
не превосходит по модулю числа 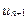 , заключаем: для вычисления числа
, заключаем: для вычисления числа 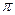 с точностью до 0,01 достаточно в равенстве (27) ограничиться первыми четырьмя членами.
с точностью до 0,01 достаточно в равенстве (27) ограничиться первыми четырьмя членами.
Таким образом, получаем:
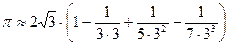 .
.
Выполнив указанные действия, находим: 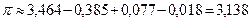 .
.
О т в е т: 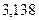 .
.
П р и м е р 12. Вычислить 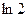 с точностью 0,0001.
с точностью 0,0001.
Р е ш е н и е. Предварительно найдем ряд Маклорена для функции
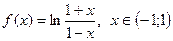 .
.
Известно, что 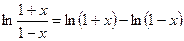 . Поэтому, пользуясь основным разложением
. Поэтому, пользуясь основным разложением
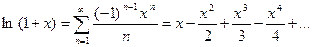 ,
,
имеем после замены х на (-х):
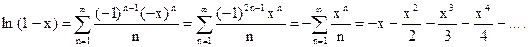
Эти ряды сходятся абсолютно при 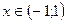 . Значит, их можно почленно вычитать. Следовательно, при
. Значит, их можно почленно вычитать. Следовательно, при 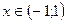 получаем:
получаем:
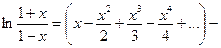
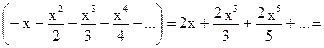
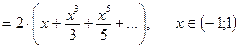 .
.
Итак, находим:
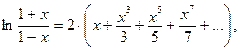
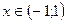 .
.
Пусть 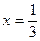 . Тогда
. Тогда 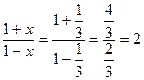 , откуда получаем:
, откуда получаем:
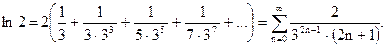 (28)
(28)
Для полученного ряда вычисляем его остаточный член:
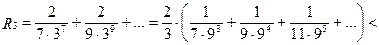
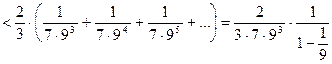
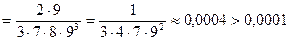 ;
;
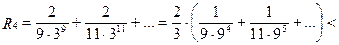
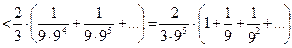
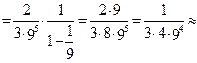
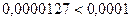 .
.
Тогда для вычисления 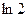 с требуемой точностью 0,0001 достаточно ограничиться в разложении (4) первыми четырьмя членами.
с требуемой точностью 0,0001 достаточно ограничиться в разложении (4) первыми четырьмя членами.
Следовательно, получаем приближенное равенство:
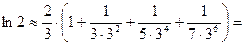
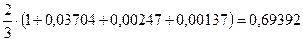 .
.
О т в е т: 0,69392.
П р и м е р 13. Найти предел: 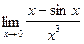 .
.
Р е ш е н и е. Вычисляем редел:
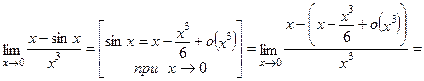
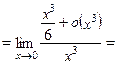
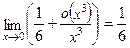 +0
+0 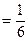 .
.
О т в е т: 1/6.
П р и м е р 14. Вычислить предел:
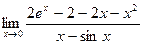 .
.
Р е ш е н и е. Подстановкой значения 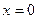 убеждаемся, что под знаком предела имеем неопределенность вида
убеждаемся, что под знаком предела имеем неопределенность вида 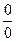 . Воспользовавшись разложениями (11) и (15), получаем:
. Воспользовавшись разложениями (11) и (15), получаем:
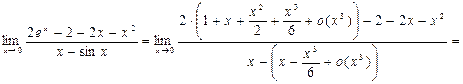
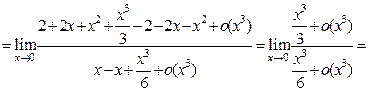
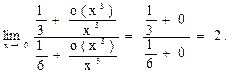
О т в е т: 2.
П р и м е р 15. Вычислить интеграл 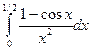 с точностью
с точностью 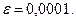
Р е ш е н и е. Используя разложение (16), получаем:
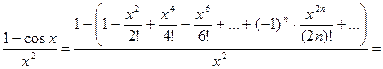
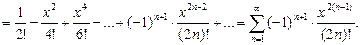
Тогда, интегрируя почленно данный ряд, находим:
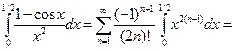
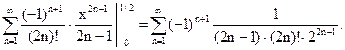 (27)
(27)
Чтобы вычислить сумму ряда (27) приближенно с точностью до 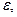 воспользуемся тем, что (27) - знакочередующийся ряд, удовлетворяющий признаку Лейбница. Следовательно, число
воспользуемся тем, что (27) - знакочередующийся ряд, удовлетворяющий признаку Лейбница. Следовательно, число 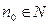 подберем так, чтобы выполнялось неравенство:
подберем так, чтобы выполнялось неравенство:
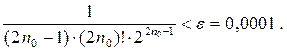
Проверкой устанавливаем, что наименьшим натуральным числом, удовлетворяющим этому неравенству, является 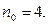 Тогда находим:
Тогда находим:
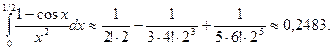
О т в е т: 0,2483.
ПРИМЕРЫ
Написать три первых члена ряда Маклорена для функций:
1. 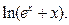 2.
2. 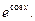 3.
3. 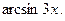
Написать три первых члена ряда Тейлора для функций:
4. 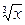 в точке
в точке 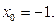 5.
5. 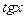 в точке
в точке 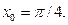
6.Разложить многочлен 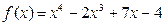 по степеням
по степеням 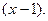
Разложить функции в ряд Тейлора, указать интервал сходимости ряда:
7. 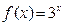 в точке
в точке 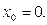 8.
8. 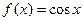 в точке
в точке 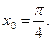
Указать ряд Маклорена функций и указать его интервал сходимости:
9. 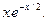 10.
10. 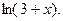 11.
11. 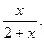 12.
12. 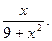 13.
13. 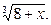 14.
14. 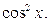
Найти ряд Тейлора функций и указать его интервал сходимости:
15. 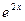 по степеням
по степеням 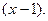 16.
16. 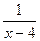 по степеням
по степеням 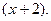
17. 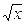 по степеням
по степеням 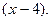 18.
18. 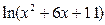 по степеням
по степеням 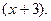
19.Вычислить 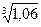 с точностью
с точностью 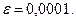
20.Вычислить 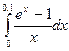 с точностью
с точностью 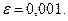
♦ ♦ ♦
21.Написать четыре первых члена ряда Маклорена для функции 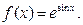
22.Разложить функцию 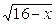 по степеням
по степеням 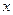 и найти интервал сходимости полученного ряда.
и найти интервал сходимости полученного ряда.
23.Разложить функцию 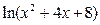 в ряд Тейлора по степеням
в ряд Тейлора по степеням 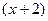 и найти область его сходимости.
и найти область его сходимости.
24. Разложить многочлен  по степеням
по степеням 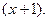
Разложить функции по степеням 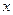 и указать интервал сходимости рядов:
и указать интервал сходимости рядов:
25. 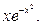 27.
27. 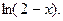 26.
26. 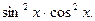 27.
27. 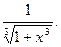 28.
28. 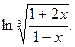 29.
29. 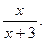
Написать разложения функций и указать интервалы сходимости рядов:
30. 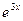 по степеням
по степеням 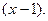 31.
31. 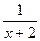 по степеням
по степеням 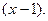
32. 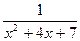 по степеням
по степеням 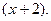 33.
33. 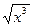 по степеням
по степеням 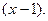
ОТВЕТЫ
1. 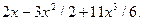 2.
2. 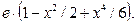 3.
3. 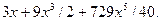
4. 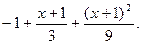 5.
5. 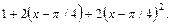 6.
6. 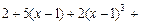
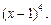
7. 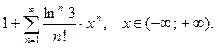
8. 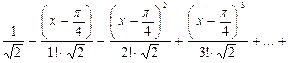
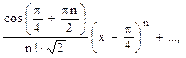
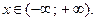
9. 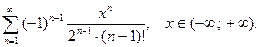 10.
10. 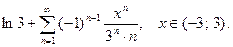
11. 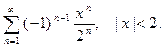 12.
12. 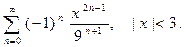
13. 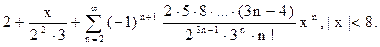
14. 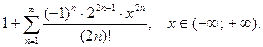 15.
15. 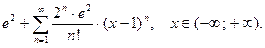
16. 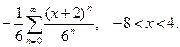 17.
17. 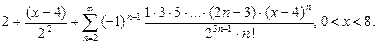
18. 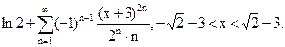 19. 1,0196. 20.0,102.
19. 1,0196. 20.0,102.
21. 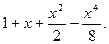 22.
22. 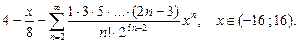
23. 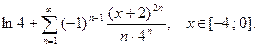 24.
24. 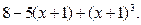
25. 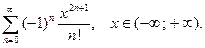 26.
26. 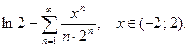
27. 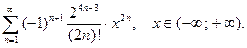 28.
28. 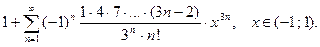
29. 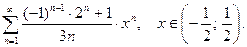 30.
30. 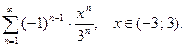
31. 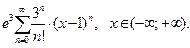 32.
32. 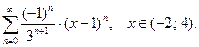
33. 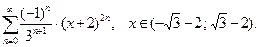
§ 11. РЯДЫ ФУРЬЕ
