Приближенные вычисления с помощью дифференциала
Рассмотрим широко распространенную задачу о приближенном вычислении значения функции с помощью дифференциала.
Здесь и далее речь пойдёт о дифференциалах первого порядка, для краткости часто будем говорить просто «дифференциал». Задача о приближенных вычислениях с помощью дифференциала обладает жёстким алгоритмом решения, и, следовательно, особых трудностей возникнуть не должно. Единственное, есть небольшие подводные камни, которые тоже будут подчищены. Так что смело ныряйте головой вниз.
Кроме того, в разделе присутствуют формулы нахождения абсолютной и относительной погрешностей вычислений. Материал очень полезный, поскольку погрешности приходится рассчитывать и в других задачах.
Для успешного освоения примеров необходимо уметь находить производные функций хотя бы на среднем уровне, поэтому если с дифференцированием совсем нелады, пожалуйста, начните с нахождения производной в точке и с нахождения дифференциала в точке. Из технических средств потребуется микрокалькулятор с различными математическими функциями. Можно использовать возможности MS Excel, но в данном случае он менее удобен.
Урок состоит из двух частей:
– Приближенные вычисления с помощью дифференциала значения функции одной переменной в точке.
– Приближенные вычисления с помощью полного дифференциала значения функции двух переменных в точке.
Рассматриваемое задание тесно связано с понятием дифференциала, но, поскольку урока о смысле производной и дифференциала у нас пока нет, ограничимся формальным рассмотрением примеров, чего вполне достаточно, чтобы научиться их решать.
Приближенные вычисления с помощью дифференциала функции одной переменной
В первом параграфе рулит функция одной переменной. Как все знают, она обозначается через y или через f(x). Для данной задачи намного удобнее использовать второе обозначение. Сразу перейдем к популярному примеру, который часто встречается на практике:
Пример 1
Вычислить приближенно 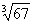 , заменяя приращения функции ее дифференциалом.
, заменяя приращения функции ее дифференциалом.
Решение: Пожалуйста, перепишите в тетрадь рабочую формулу для приближенного вычисления с помощью дифференциала:
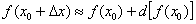
Начинаем разбираться, здесь всё просто!
На первом этапе необходимо составить функцию 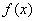 . По условию предложено вычислить кубический корень из числа:
. По условию предложено вычислить кубический корень из числа: 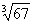 , поэтому соответствующая функция имеет вид:
, поэтому соответствующая функция имеет вид: 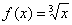 .
.
Нам нужно с помощью формулы найти приближенное значение 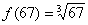 .
.
Смотрим на левую часть формулы 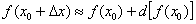 , и в голову приходит мысль, что число 67 необходимо представить в виде
, и в голову приходит мысль, что число 67 необходимо представить в виде 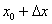 . Как проще всего это сделать? Рекомендую следующий алгоритм: вычислим данное значение на калькуляторе:
. Как проще всего это сделать? Рекомендую следующий алгоритм: вычислим данное значение на калькуляторе:
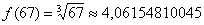 – получилось 4 с хвостиком, это важный ориентир для решения.
– получилось 4 с хвостиком, это важный ориентир для решения.
В качестве x0 подбираем «хорошее» значение, чтобы корень извлекался нацело. Естественно, это значение x0 должно быть как можно ближек 67.
В данном случае x0 = 64. Действительно, 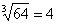 .
.
Примечание: Когда с подбором x0 всё равно возникает затруднение, просто посмотрите на скалькулированное значение (в данном случае 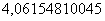 ), возьмите ближайшую целую часть (в данном случае 4) и возведите её нужную в степень (в данном случае
), возьмите ближайшую целую часть (в данном случае 4) и возведите её нужную в степень (в данном случае 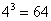 ). В результате и будет выполнен нужный подбор x0 = 64.
). В результате и будет выполнен нужный подбор x0 = 64.
Если x0 = 64, то приращение аргумента: 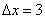 .
.
Итак, число 67 представлено в виде суммы 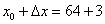
Далее работаем с правой частью формулы 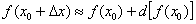 .
.
Сначала вычислим значение функции в точке x0 = 64. Собственно, это уже сделано ранее:
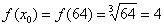 .
.
Дифференциал в точке находится по формуле:
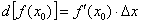 – эту формулу тоже можете переписать к себе в тетрадь.
– эту формулу тоже можете переписать к себе в тетрадь.
Из формулы следует, что нужно взять первую производную:
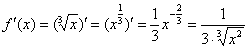
И найти её значение в точке x0:
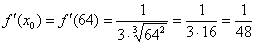 .
.
Таким образом:
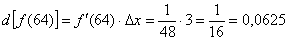
Всё готово! Согласно формуле 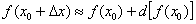 :
:
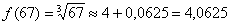
Найденное приближенное значение достаточно близко к значению 4,06154810045, вычисленному с помощью микрокалькулятора.
Ответ: 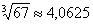
Пример 2
Вычислить приближенно 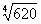 , заменяя приращения функции ее дифференциалом.
, заменяя приращения функции ее дифференциалом.
Это пример для самостоятельного решения. Примерный образец чистового оформления и ответ в конце урока. Начинающим сначала рекомендую вычислить точное значение 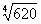 на микрокалькуляторе, чтобы выяснить, какое число принять за x0, а какое – за Δx. Следует отметить, что Δx в данном примере будет отрицательным.
на микрокалькуляторе, чтобы выяснить, какое число принять за x0, а какое – за Δx. Следует отметить, что Δx в данном примере будет отрицательным.
У некоторых, возможно, возник вопрос, зачем нужна эта задача, если можно всё спокойно и более точно подсчитать на калькуляторе? Согласен, задача глупая и наивная. Но попытаюсь немного её оправдать. Во-первых, задание иллюстрирует смысл дифференциала функции. Во-вторых, в древние времена калькулятор был чем-то вроде личного вертолета в наше время. Сам видел, как из одного из институтов году где-то в 1985-86 выбросили компьютер размером с комнату (со всего города сбежались радиолюбители с отвертками, и через пару часов от агрегата остался только корпус). Антиквариат водился и у нас на физфаке, правда, размером поменьше – где-то с парту. Вот так вот и мучились наши предки с методами приближенных вычислений. Конная повозка – тоже транспорт.
Так или иначе, задача осталась в стандартном курсе высшей математики, и решать её придётся. Это основной ответ на ваш вопрос =).
Пример 3
Вычислить приближенно с помощью дифференциала значение функции 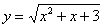 в точке x = 1,97. Вычислить более точное значение функции в точке x = 1,97 с помощью микрокалькулятора, оценить абсолютную и относительную погрешность вычислений.
в точке x = 1,97. Вычислить более точное значение функции в точке x = 1,97 с помощью микрокалькулятора, оценить абсолютную и относительную погрешность вычислений.
Фактически, это задание запросто можно переформулировать так: «Вычислить приближенное значение 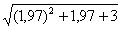 с помощью дифференциала»
с помощью дифференциала»
Решение:Используем знакомую формулу: 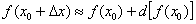
В данном случае уже дана готовая функция: 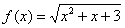 . Ещё раз обращаю внимание, что для обозначения функции вместо «игрека» удобнее использовать f(x).
. Ещё раз обращаю внимание, что для обозначения функции вместо «игрека» удобнее использовать f(x).
Значение x = 1,97 необходимо представить в виде x0 = Δx. Ну, тут легче, мы видим, что число 1,97 очень близко к «двойке», поэтому напрашивается x0 = 2. И, следовательно: 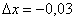 .
.
Вычислим значение функции в точке x0 = 2:
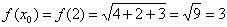
Используя формулу 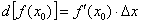 , вычислим дифференциал в этой же точке.
, вычислим дифференциал в этой же точке.
Находим первую производную:
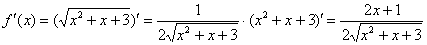
И её значение в точке x0 = 2:
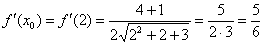
Таким образом, дифференциал в точке:
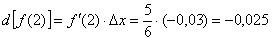
В результате, по формуле 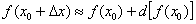 :
:
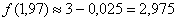
Вторая часть задания состоит в том, чтобы найти абсолютную и относительную погрешность вычислений.
