Приближенные вычисления с помощью бинома Ньютона

Положим в формуле бинома Ньютона :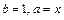

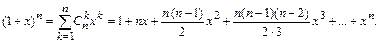
Эту формулу удобно применять для приближенных вычислений при малых значениях x ( ).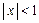

Пример 1. Используя формулу бинома Ньютона, вычислить 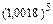с точностью до .

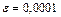По приведенной выше формуле имеем:

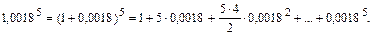
Оценим третье слагаемое в этой сумме.

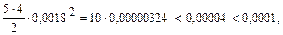
остальные слагаемые еще меньше. Поэтому все слагаемые, начиная с третьего, можно отбросить. Тогда

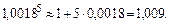
Пример 2. Вычислить 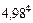с точностью до 0,01.

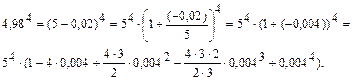
Оценим третье слагаемое:

.

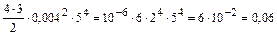Оценим четвертое слагаемое:

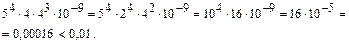
Значит все слагаемые, начиная с четвертого, можно отбросить. Получим

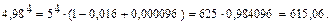
2.1.14. Контрольные вопросы и упражнения

1. Выборка, среди элементов которой нет одинаковых, а порядок записи элементов важен, является ______________________ .

2. Выборка, среди элементов которой нет одинаковых, а порядок записи элементов безразличен, является ________________________ .

3. Количество размещений с повторениями из n элементов по r элементов определяется по формуле

__________ = ________________________ .

4. Количество сочетаний из n элементов по r элементов определяется по формуле

____________ = ________________________ .

5. Сформулируйте основные правила комбинаторики.

6. Сколькими способами можно выбрать конверт и марку для письма, если имеется 5 конвертов и 4 марки?

7. Сколько пятизначных номеров можно составить из девяти цифр {1,2,3,4,5,6,7,8,9}?

8. Сколькими способами можно составить трехцветный полосатый флаг (все полосы горизонтальные), если имеются ткани пяти различных цветов?

9. Сколькими способами могут расположиться в турнирной таблице 7 футбольных команд, если известно, что все команды набрали различное количество очков?

10. Сколькими способами можно составить команду из 4 человек, если имеется 7 бегунов?

11. Сколькими способами можно разложить 12 различных предметов по четырем различным ящикам так, чтобы в каждом ящике оказалось по три предмета?

12. Сколькими способами можно разложить 6 одинаковых шаров по четырем различным ящикам?

13. Запишите разложение бинома .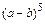

14. Докажите свойство симметрии биномиальных коэффициентов, сравнив формулы для 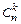и .

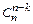15. Найдите максимальный числовой коэффициент в разложении бинома .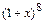

16. Пользуясь формулой бинома Ньютона, вычислите 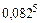с точностью до .

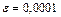Группы подстановок

Понятие группы

Теория групп начала оформляться в качестве самостоятельного раздела математики в конце VIII века. Она дала мощные средства для исследования алгебраических уравнений, геометрических преобразований, а также для решения ряда задач топологии и теории чисел. Специалисты, занимающиеся обработкой информации, используют методы теории групп при кодировании и декодировании информации.

Мы рассмотрим лишь небольшую часть теории групп и некоторые ее приложения. Наша первая задача – выяснить, что же такое группа.

Для этого сначала определим понятие бинарной алгебраической операции.

Бинарная операция на множестве – это соответствие, при котором каждой упорядоченной паре элементов данного множества отвечает однозначно определенный элемент того же множества. Так, действие сложения есть бинарная операция на множестве целых чисел; в самом деле, если r и s – любые два целых числа, то 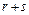тоже является целым числом.

Определение 1. Непустое множество G с заданной на нем бинарной алгебраической операцией Ä называется группой, если:

1) операция Ä ассоциативна;

2) существует единичный элемент 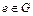такой, что для каждого 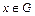выполняется условие: ;

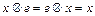3) для каждого 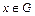существует обратный элемент 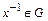такой, что .

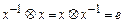Эти три условия, необходимые для того, чтобы множество G с заданной на нем операцией Ä являлось группой, называются аксиомами группы.

Пример 1. Рассмотрим в качестве множества G множество всех целых чисел Z, а в качестве бинарной операции – сложение.

Проверим для пары (Z, +) аксиомы группы.

1) Ассоциативность. Сложение чисел ассоциативно: для любых 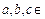Z, ;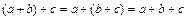

2) Единичный элемент: нуль является единичным элементом для рассматриваемого множества относительно операции сложения, так как для каждого 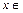Z выполняется условие: ;

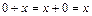3) Обратный элемент: для каждого 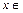Z существует элемент –x, такой, что .

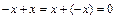Итак, проверка показывает, что (Z, +) – группа.

Пример 2. Рассмотрим то же множество Z, но теперь с операцией умножения, т.е. рассмотрим пару (Z, ·). Проверим аксиомы группы.

1) Ассоциативность. Умножение чисел ассоциативно: для любых 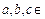Z, ;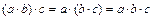

2) Единичный элемент: число 1 является единичным элементом рассматриваемого множества относительно операции умножения, т.е. для каждого 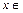Z выполняется условие: ;

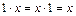3) Обратный элемент. Так как аксиома должна выполняться для любого элемента множества Z, то попытаемся найти обратный элемент для числа 2, т.е. нужно найти 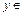Z, такой что 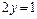или 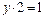. Такого целого числа не существует, таким образом, множество целых чисел, с заданной на нем операцией умножения, не является группой.

Определение 2. Множество 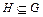называется подгруппой группы G, если оно замкнуто относительно операции Ä, 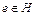, и для каждого 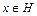обратный элемент .

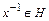Группа подстановок

Пусть множество X состоит из n элементов 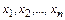, расположенных в произвольном, но фиксированном порядке.

Биекция 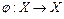называется подстановкой.

В случаях, когда природа элементов не имеет значения, удобно обращать внимание только на индексы и считать, что мы имеем дело с множеством 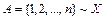. Следовательно,

.

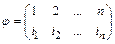Обозначим 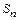- множество всех подстановок на A. Очевидно, что .

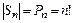На множестве 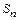будем рассматривать операцию перемножения (композиции) подстановок 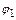и :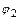

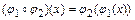для любого .

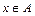Эта операция обладает свойствами:

1) 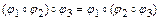- выполняется свойство ассоциативности;

2) существует подстановка 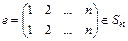, для которой 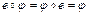для каждого 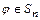- выполняется аксиома существования единичного элемента;

3) для любого 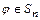существует 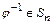такое, что 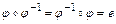- выполняется аксиома существования обратного элемента.

Следовательно, множество 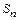образует группу относительно операции перемножения перестановок. Отметим, что эта операция не является коммутативной, то есть 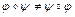, например,

,

.

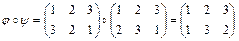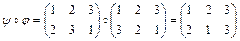Рассмотрим произвольную подстановку 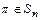. Элемент 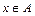такой, что 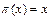будем называть стационарным относительно подстановки 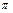. Пусть 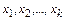- все нестационарные элементы подстановки 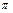, причем, 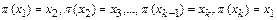, где k – наименьшее из всех возможных. Такая подстановка называется циклом длины k и записывается в виде .

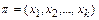Пример 1. Пусть .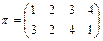

Стационарный элемент 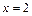. Подстановка 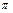является циклом длины 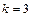и может быть записана в виде .

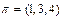Пример 2. Пусть .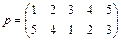

Подстановка p не является циклом, но может быть представлена в виде композиции двух циклов:

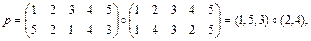
причем эти циклы являются непересекающимися, т.е. не имеют общих нестационарных элементов.

Теорема 1. Любая подстановка 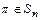может быть представлена в виде композиции непересекающихся циклов длины :

.

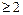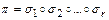Доказательство теоремы дает процедуру построения циклов.

Найдем в A наименьший нестационарный относительно 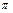элемент 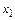, т.е. 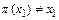и для каждого 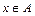выполняется условие: если 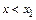, то 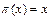. (Если такого элемента не существует, то 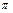является тождественной подстановкой ( 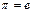) и ее можно рассматривать как пустое произведение циклов).

Будем строить образы элемента 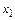, 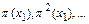до тех пор, пока не получим 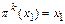при наименьшем из возможных k ( 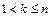). Тогда подстановка

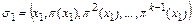
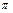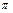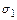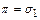определяет цикл длины k внутри подстановки . Если все нестационарные элементы подстановки содержатся в , то . В противном случае найдем 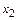- наименьший из нестационарных элементов подстановки 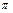, не входящий в цикл 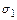. Строим цикл

.

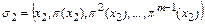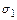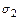Очевидно, что и - непересекающиеся. Если все нестационарные элементы исчерпаны, то 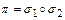, в противном случае повторяем процесс, пока каждый нестационарный элемент не войдет в какой-либо цикл. В конечном итоге получим .

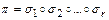Пример. Представить в виде композиции циклов подстановку

.

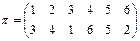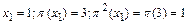, значит ;

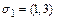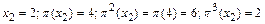,значит ;

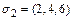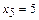- стационарный элемент.

Следовательно, .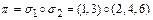

Определение. Порядком подстановки 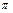называется наименьшее натуральное число p такое, что .

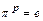Теорема 2. Порядок подстановки равен наименьшему общему кратному порядков циклов в ее разложении на непересекающиеся циклы.

В качестве упражнения предлагается провести доказательство теоремы самостоятельно.

Изоморфизм групп

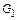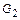Определение. Группы и называются изоморфными, если существует биекция 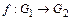, сохраняющая групповую операцию, т.е.

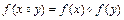
для всех .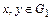

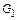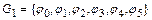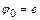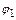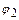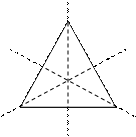
Пример. Пусть - группа преобразований правильного треугольника в себя , где - тождественное преобразо-вание, - поворот вокруг точки O на 120°, - поворот вокруг точки O на 240°, 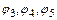- отражение относительно осей симметрии I, II, III соответственно (рис. 2.3).

2

III I

1 3

II

Рис. 2.3. Преобразование правильного треугольника

В качестве группы 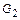рассмотрим группу подстановок на множестве 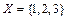вершин треугольника 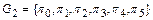, где

, , ,

, , .

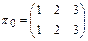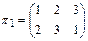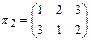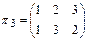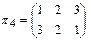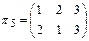Легко убедиться, что биекция 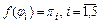группы 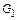на группу 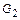является изоморфизмом.

Будем называть порядком конечной группы 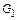количество ее элементов .

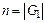Теорема (Кэли). Всякая конечная группа порядка n изоморфна некоторой подгруппе группы подстановок .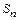

Доказательство. Пусть 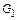произвольная подгруппа порядка n. Обозначим 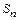группу подстановок на множестве 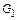. Зафиксируем произвольный элемент 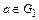и рассмотрим отображение 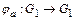такое, что 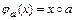для любого 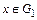. Очевидно, образы различных элементов x и y, принадлежащих 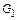, различны и, следовательно, множество значений 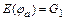. Действительно, предположим, что 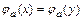при 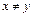. Тогда .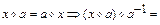

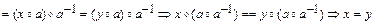Значит, отображение 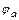является подстановкой на множестве 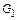, причем 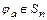, , 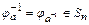, 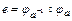т.е. множество 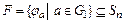образует подгруппу группы 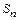. При этом

.

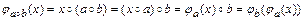Следовательно, отображение 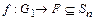такое, что 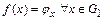является изоморфизмом, т.к. .

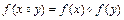Задача. Найти группу подстановок, изоморфную группе поворотов правильного восьмиугольника на плоскости.

Решение задачи провести самостоятельно.

Самосовмещения фигур

Обширный и очень важный класс разнообразных групп как конечных, так и бесконечных составляют группы “самосовмещений” геометрических фигур. Под самосовмещением данной геометрической фигуры F понимают такое перемещение фигуры F (в пространстве или на плоскости), которое переводит F в самое себя, т.е. совмещает фигуру F с самой собой.

Мы уже познакомились с одной из простейших групп самосовмещений, а именно с группой поворотов правильного треугольника на плоскости и показали, что она изоморфна некоторой подгруппе группы подстановок 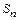. Аналогичным образом можно построить группы самосовмещений других геометрических фигур и показать их изоморфизм с подгруппой группы .

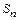Задача. Построить группу симметрий квадрата.

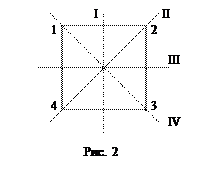
Решение. Занумеруем вершины квадрата и оси симметрий (рис. 2.4). Обозначим O – центр симметрии квадрата.

В группу самосовмещений войдет тождественное перемещение – поворот вокруг точки O на 0°; повороты вокруг этой точки на 90°, на 180° и на 270°; повороты относительно четырех осей симметрии. Итого, получаем восемь элементов группы симметрий.

Тождественное перемещение описывает тождественная подстановка 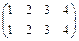. Вращения на 90°, на 180° и на 270° - подстановк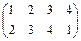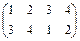и , и 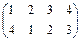соответственно.

Поворот относительно оси I описывает подстановка 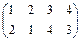; относительно оси II – подстановка 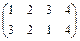; оси III - 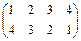; оси IV - .

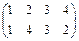Таким образом, мы получили группу подстановок, изоморфную группе самосовмещений квадрата:

S₈ =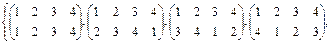

.

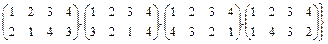2.2.5. Контрольные вопросы и упражнения

1. Что такое группа?

2. Дано множество 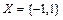. Проверить, является ли данное мно-жество группой относительно операции умножения.

3. Что такое подгруппа?

4. Привести пример подстановки, которая является полным циклом.

5. Объяснить процедуру разложения подстановки в произведение независимых циклов.

6. Чему равен порядок подстановки ?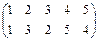

7. Какие группы называются изоморфными?

8. Приведите примеры самосовмещений геометрических фигур.