Задача 6. Смешанные задачи на дифференциальные уравнения первого порядка.
Смешанные задачи на дифференциальные уравнения первого порядка.
Определить тип дифференциального уравнения и указать в общем виде метод его решения:
Пример7.
а)  . Ответ: однородное:
. Ответ: однородное: 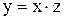 .
.
б)  . Ответ: в полных дифферен-
. Ответ: в полных дифферен-
циалах.
в)  . Ответ: линейное,
. Ответ: линейное,  .
.
г)  .
.
Ответ: Бернулли,  .
.
Упражнения.
Определить тип уравнения и указать в общем виде метод решения:
1.  . Ответ: линейное,
. Ответ: линейное,  или
или
 .
.
2.  . Ответ: Бернулли,
. Ответ: Бернулли,  .
.
3.  . Ответ: однородное,
. Ответ: однородное, 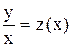 .
.
4.  . Ответ: в полных дифферен-
. Ответ: в полных дифферен-
циалах.
Определить тип уравнения и указать в общем виде метод решения:
1.  . . |
2.  . . |
3.  . . |
4.  . . |
5.  . . |
6.  . . |
7.  . . |
8.  . . |
9.  . . |
10.  . . |
11.  . . |
12.  . . |
13.  |
14.  . . |
15.  . . |
16.  . . |
17.  . . |
18.  . . |
19.  . . |
20.  . . |
21.  . . |
22.  . . |
23.  . . |
24.  . . |
25.  . . |
26.  . . |
27.  . . |
28.  . . |
29.  . . |
30.  . . |
Задача 7. Смешанные задачи на дифференциальные уравнения первого порядка.
Упражнения. Определить тип уравнения и решить его:
1.  . Ответ: с разделяющимися переменными,
. Ответ: с разделяющимися переменными,
 .
.
2.  . Ответ: однородное,
. Ответ: однородное,  .
.
3.  . Ответ: линейное,
. Ответ: линейное,  .
.
4.  . Ответ: Бернулли,
. Ответ: Бернулли,  .
.
Определить тип уравнения и решить:
| 1. |  . . |
| 2. |  . . |
| 3. |  . . |
| 4. |  . . |
| 5. |  . . |
| 6. |  . . |
| 7. |  . . |
| 8. |  . . |
| 9. |  . . |
| 10. |  . . |
| 11. |  . . |
| 12. | 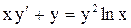 . . |
| 13. |  . . |
| 14. |  . . |
 . . | |
| 16. |  . . |
| 17. |  . . |
| 18. |  . . |
| 19. |  . . |
| 20. |  . . |
| 21. |  . . |
| 22. |  . . |
| 23. |  . . |
| 24. |  . . |
| 25. |  . . |
| 26. |  . . |
| 27. |  . . |
| 28. |  . . |
| 29. |  . . |
| 30. |  . . |
Задача 8. Дифференциальные уравнения высших порядков, допускающие понижение порядка.
Укажем три вида дифференциальных уравнений, допускающих понижение порядка
I. Уравнение вида
 (1)
(1)
После n– кратного интегрирования получается общее решение.
II. Уравнение не содержащее искомой функции и ее производных до порядка  включительно
включительно
 . (2)
. (2)
Порядок такого уравнения можно понизить на  единиц заменой
единиц заменой
 .
.
Тогда уравнение (2) примет вид  .
.
Из последнего уравнения, если это возможно, определяют  , а затем находят
, а затем находят 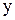 из уравнения
из уравнения
 ,
,
 – кратным интегрированием.
– кратным интегрированием.
III. Уравнение не содержит независимого переменного
 . (3)
. (3)
Подстановка  , позволяет понизить порядок уравнения на единицу. Все производные выражаются через производные от новой функции
, позволяет понизить порядок уравнения на единицу. Все производные выражаются через производные от новой функции  :
:

Пример 8.
Найти общее решение уравнения  .
.
Решение.
 ,
,
 ,
,
 .
.
Пример 9. Решить уравнение  .
.
Решение.
Данное уравнение не содержит искомой функции 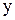 и ее производной, уравнение II типа. Полагаем
и ее производной, уравнение II типа. Полагаем  , тогда
, тогда  . После этого уравнения примет вид
. После этого уравнения примет вид  .
.
Разделяя переменные, найдем  , заменяя на
, заменяя на  , получим
, получим  . Интегрируя последовательно, будем иметь
. Интегрируя последовательно, будем иметь

 .
.
Ответ:  .
.
Пример 10. Решить уравнение  .
.
Решение.
Данное уравнение III типа. Введем обозначение  , получим
, получим  - уравнение Бернулли. Подстановкой
- уравнение Бернулли. Подстановкой  оно сводится к линейному уравнению
оно сводится к линейному уравнению  .
.

Заменяя 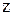 на
на  , получим
, получим  . Интегрируя, будем иметь
. Интегрируя, будем иметь
 или
или  ;
;  .
.
Замечание. При решении задачи Коши для уравнений высших порядков целесообразно определять значения постоянных  в процессе решения, а не после нахождения общего решения уравнения.
в процессе решения, а не после нахождения общего решения уравнения.
Пример 11. Решить задачу Коши  .
.
Решение.
Полагая  , получим
, получим  или
или  откуда
откуда  ;
;  .
.
Разделяя переменные, найдем  . Интеграл в правой части в элементарных функциях не вычисляется, как интеграл от дифференциаль-
. Интеграл в правой части в элементарных функциях не вычисляется, как интеграл от дифференциаль-
ного бинома, случай неберущегося интеграла.
Но если использовать начальные условия  , то
, то  и тогда
и тогда

Ответ:  .
.
Упражнения. Решить уравнения.
1)  . Ответ:
. Ответ:  .
.
2)  . Ответ:
. Ответ:  .
.
3)  . Ответ:
. Ответ:  .
.
4)  . Ответ:
. Ответ:  .
.
Решить уравнения, допускающие понижение порядка
| 1. |  . . |
| 2. |  . . |
| 3. |  . . |
| 4. |  . . |
| 5. |  . . |
| 6. |  . . |
| 7. |  . . |
| 8. |  . . |
| 9. |  . . |
| 10. |  . . |
| 11. |  . . |
| 12. |  . . |
| 13. |  . . |
| 14. |  . . |
| 15. |  . . |
| 16. |  . . |
| 17. |  . . |
| 18. |  . . |
| 19. |  . . |
| 20. |  . . |
| 21. |  . . |
| 22. |  . . |
| 23. |  . . |
| 24. |  . . |
| 25. |  . . |
| 26. |  . . |
| 27. |  . . |
| 28. |  . . |
| 29. |  . . |
| 30. |  . . |
Задача 9. Линейные дифференциальные уравнения 2– го и n–го порядка.
