Дифференциальные уравнения первого порядка. Теорема о существовании и единственности решения.

Дифференциальным уравнением первого порядка называется уравнение, связывающее независимую переменную x, искомую функцию y(x) и производную первого порядка искомой функции.
Дифференциальное уравнение первого порядка имеет вид .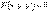

Теорема Коши:Если функция f(x,y) - правая часть дифференциального уравнения y ^I = f(x,y) - непрерывна в некоторой замкнутой области D плоскости xOy и имеет в этой области ограниченную частную производную f ^I_y (x,y), то каждой внутренней точке области D соответствует, и притом единственное, решение, удовлетворяющее начальным условиям.

Дифференциальные уравнения с разделяющимися переменными.

Дифференциальные уравнения 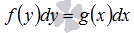называют уравнениями с разделенными переменными.

Название этого вида дифференциальных уравнений достаточно показательно: выражения, содержащие переменные x и y, разделены знаком равенства, то есть, находятся по разные стороны от него.

Будем считать, что функции f(y) и g(x) непрерывны.

Общим интегралом уравнения с разделенными переменными является равенство 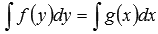. Если интегралы из этого равенства выражаются в элементарных функциях, то мы можем получить общее решение дифференциального уравнения как неявно заданную функцию Ф(x, y) = 0, а иногда получается выразить функцию y в явном виде.

Однородные дифференциальные уравнения первого порядка.

Существует два понятия однородности дифференциальных уравнений.

Обыкновенное уравнение первого порядка 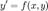называется однородным относительно x и y, если функция 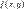является однородной степени 0 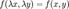.Однородную функцию можно представить как функцию от 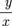: 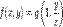.Используем подстановку 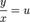, а затем воспользуемся правилом произведения : 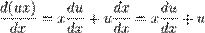. Тогда, дифференциальное уравнение 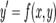сводится к уравнению с разделяющимися переменными: 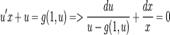.Дифференциальное уравнение является однородным, если оно не содержит свободного члена — слагаемого, не зависящего от неизвестной функции. Так, можно говорить, что уравнение 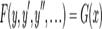— однородно, если 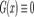.В случае, если 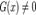, говорят о неоднородном дифференциальном уравнении.Именно для решения линейных однородных диф. уравнений была построена целая теория, чему способствовало выполнение у них принципа суперпозиции

Линейные дифференциальные уравнения первого порядка.

Линейное дифференциальное уравнение первого порядка с переменными коэффициентами имеет общий вид

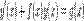Уравнения в такой форме могут быть решены путём умножения на интегрирующий множитель

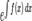получим 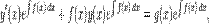используем правило дифференцирования произведения 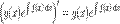что, после интегрирования обеих частей, дает нам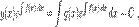 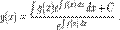Таким образом, решение линейного дифференциального уравнения первого порядка 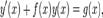(в частности, с постоянными коэффициентами) имеет вид

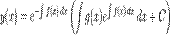где является константой интегрирования.