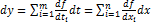Вопрос 15 Частные производные. Дифференцируемость ф-ций неск. переменных, осн. теоремы, необ. и достат. условие дифф-ти, дифф-ие сложной ф-ции, инвар-ть формы 1-ого диф-ла.
Функция называется дифференцируемой в данной точке, если ее полное приращение в этой точке может быть представлено в виде: 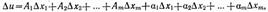 , где А1, А2, …, Аm – некоторые не зависящие от ∆х1, ∆х2, …, ∆хm числа, а α1, α2, …, αm – бесконечно малые при
, где А1, А2, …, Аm – некоторые не зависящие от ∆х1, ∆х2, …, ∆хm числа, а α1, α2, …, αm – бесконечно малые при 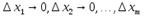 функции, равные 0 при ∆х1=∆х2=…∆хm=0.
функции, равные 0 при ∆х1=∆х2=…∆хm=0.
Частная производная функции z=f(x,y) по х – предел отношения частного приращения функции по х к приращению Δх при Δх→0, если он существует и конечен:
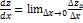
Частная производная функции z=f(x,y) по y- – предел отношения частного приращения функции по y к приращению Δy при Δy→0, если он существует и конечен:
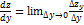
Полный дифференциал функции z=f(x,y) - главная линейная относительно  и ∆у часть приращения функции ∆z в точке (х,у): dz= fx(x,y)dx+ fy (x,y)dy
и ∆у часть приращения функции ∆z в точке (х,у): dz= fx(x,y)dx+ fy (x,y)dy
Если функция f(x,y) определена в некоторой области D, то её частные производные f ’x(x,y), f ’y(x,y), тоже будут определены в той же области или её части. Будем называть эти производные производными I-ого порядка. Производные этих функций производными II-ого порядка.
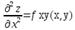
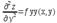
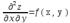
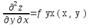
Необх. и дост. условие дифференцируемости
Напомним, что функция одной переменной 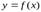 называется дифференцируемой в точке
называется дифференцируемой в точке 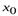 , если приращение функции представимо в виде
, если приращение функции представимо в виде
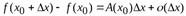 ,
,
где 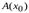 ― некоторое действительное число, зависящее от
― некоторое действительное число, зависящее от 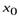 , а
, а 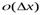 -бесконечно малая функция более высокого порядка малости, чем
-бесконечно малая функция более высокого порядка малости, чем 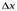 , при
, при 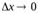 .
.
Необходимым и достаточным условием дифференцируемости функции 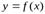 в точке
в точке 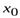 является существование производной
является существование производной
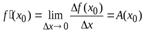 .
.
Выясним, как переносятся условия дифференцируемости на случай функции двух переменных.
Определение.Функция 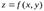 называется дифференцируемой в точке
называется дифференцируемой в точке 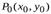 , если ее полное приращение в этой точке можно представить в виде
, если ее полное приращение в этой точке можно представить в виде
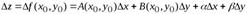 ,(1)
,(1)
Дифференцирование сложной ф-ции
Пусть задана функция двух переменных 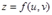 и пусть переменные
и пусть переменные 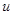 и
и 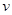 сами являются непрерывными функциями независимых переменных
сами являются непрерывными функциями независимых переменных 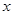 и
и 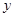 :
: 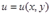 ,
, 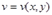 . (*)
. (*)
Таким образом,
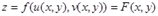 ,
,
т.е. 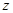 является сложной функцией переменных
является сложной функцией переменных  и
и 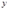 . Выясним, как найти ее частные производные по аргументам
. Выясним, как найти ее частные производные по аргументам 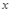 и
и 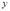 , не делая непосредственной подстановки. При этом будем предполагать, что все рассматриваемые функции имеют непрерывные частные производные по всем своим аргументам. Сначала найдем производную
, не делая непосредственной подстановки. При этом будем предполагать, что все рассматриваемые функции имеют непрерывные частные производные по всем своим аргументам. Сначала найдем производную 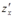 . Для этого дадим аргументу
. Для этого дадим аргументу 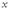 приращение
приращение 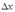 , сохраняя значение
, сохраняя значение 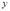 неизменным. Тогда в силу уравнений (*) получат приращения
неизменным. Тогда в силу уравнений (*) получат приращения 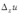 и
и 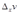 .
.
Но если 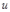 и
и 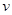 получают приращения
получают приращения 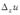 и
и 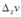 , то функция
, то функция 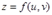 получит приращение
получит приращение 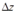 , определяемое формулой:
, определяемое формулой:
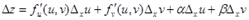 .
.
Разделим обе части последнего равенства на 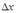 :
:
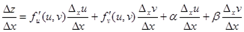 .
.
Если 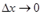 , то
, то 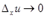 и
и 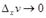 (в силу непрерывности функций
(в силу непрерывности функций 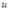 и
и 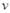 ). Но тогда
). Но тогда 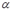 и
и 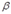 тоже стремятся к нулю. Переходя к пределу при
тоже стремятся к нулю. Переходя к пределу при 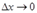 , получим
, получим
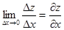 ,
, 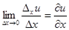 ,
, 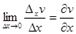 ,
,
и, следовательно,
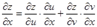 . (1)
. (1)
Аналогично находим производную  по переменной
по переменной 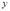 :
:
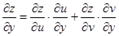 . (2)
. (2)
Вывод. Частная производная сложной функции равна сумме произведений частных производных заданной функции по промежуточным аргументам ( 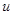 и
и 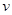 ) на частные производные этих аргументов (
) на частные производные этих аргументов ( 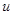 и
и 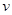 ) по соответствующей независимой переменной (
) по соответствующей независимой переменной ( 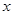 и
и 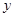 ), где
), где 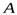 и
и 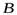 — некоторые постоянные, зависящие от
— некоторые постоянные, зависящие от 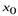 и
и 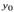 ;
; 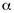 и
и 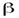 — функции от
— функции от 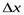 и
и 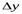 , стремящиеся к нулю при
, стремящиеся к нулю при 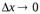 и
и 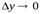 , то есть
, то есть 
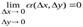 ,
, 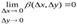 .
.
Равенство (1) выражает условие дифференцируемости функции 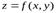 в точке
в точке 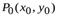 .
.
Определение.Функцию 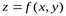 , дифференцируемую в каждой точке некоторого множества, называют дифференцируемой на этом множестве.
, дифференцируемую в каждой точке некоторого множества, называют дифференцируемой на этом множестве.
Инвариантность формы 1-ого диф-ла
Если xi(t) непрерывно диф-ма на t= t0(t01+ t02 +…+ t0m), а y=f(x); x=(x1,x2,…xn) непрерыв.. диф-ма в т. x0=(x01,x02,…x0n), xoi (to), то ф-ция y=f(x(t)) диф-ма в точке tо и справедливо равенство