Оценка математического ожидания, моды, медианы и дисперсии
Задание 24. Условно считая числа, данные в задании 5, как некий ранжированный (упорядоченный по возрастанию) ряд вероятностного распределения признака Х некой генеральной совокупности, оценить: 1) математическое ожидание, 2) моду, 3) медиану и 4) дисперсию распределения. Построить закон распределения, полигон и гистограмму распределения признака Х.
Решение. Пусть у нас вариант 32. В задании 5 имеем ряд: 1,1,2,3,3,3.
КРАТКАЯ ТЕОРИЯ.
Определение 1. Генеральной средней 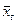 (или а) называется среднее арифметическое значений признака генеральной совокупности.
(или а) называется среднее арифметическое значений признака генеральной совокупности.
Если все значения x1, x2, …, xN признака генеральной совокупности объема N различны, то 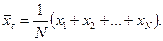
Определение 2. Генеральной дисперсией Dг. называют среднее арифметическое квадратов отклонений значений признака X генеральной совокупности от генеральной средней 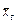 .
.
Если все значения x1, x2, …, xN признака генеральной совокупности объема N различны, то 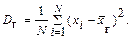
КОНЕЦ КРАТКОЙ ТЕОРИИ.
Решение.
1) Математическое ожидание равно среднему арифметическому из всех значений: 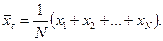 ,
, 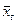 =(1+1+2+3+3+3)/6=13/6»2,2167.
=(1+1+2+3+3+3)/6=13/6»2,2167.
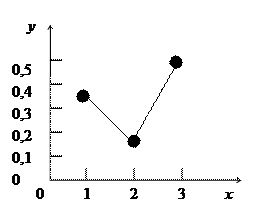
2) Мода – это наивероятнейшее значение или вершина на графике распределения, оно равно xmod=3 (встречается чаще других – 3 раза). Другая мода – изолированная вершина на графике равна xmod=1.
3) Медиана – это такое воображаемое или реальное значение, которое делит ранжированный ряд на две равные части. Наш ранжированный ряд можно разбить две равные по числу значений части: {1,1,2} и {3,3,3}. Очевидно, что медиана находится строго на середине внутренних границ этих частей, выделенных жирным шрифтом:2 и 3 . Т.е. медиана равна их полусумме: xmed= (2+3)/2=2,5.
4) Дисперсию оценим по формуле: 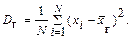 имеем
имеем
Dг= [(1-2,2167)2+(1-2,2167) 2+(2-2,2167) 2+(3-2,2167) 2+(3-2,2167) 2+(3-2,2167) 2]/6=
= [(-1,2167)2+(-1,2167) 2+0,2167 2+0,7833 2+0,7833 2+0,7833 2]/6=
=(2×1,48035889+0,04695889+3×0,61355889)/6=
=(2,96071778+0,04695889+1,84067667)/6=4,84835334/6»0,80805889
5) Ответы: 1) 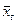 »2,2167, 2) xmod=3, 3) xmed=2,5,4) Dг»0,808.
»2,2167, 2) xmod=3, 3) xmed=2,5,4) Dг»0,808.
Наша случайная величина задана законом распределения
| Варианта хi | Сумма | |||
| Абсолютная частота ni | n=6 | |||
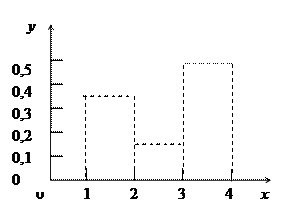
| Относительная частота pi | 0,333 | 0,167 | 0,500 |
Относительные частоты pi находим по формулам pi= ni / n.
Имеем p1= n1 / n=2/6=0,333, p2= n2 / n=1/6=0,167, , p3= n3 / n=3/6=0,500.
Полигоном и гистограмма распределения признака Х построены на рис. ниже.
 |  |
Задание 25.Случайная величина X задана плотностью вероятности
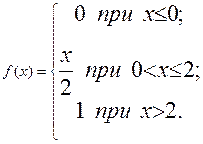
Оценить: 1) математическое ожидание, 2) моду, 3) медиану и 4) дисперсию распределения. Построить закон распределения, полигон и гистограмму распределения признака Х.
Решение. Согласно определениям математического ожидания непрерывной случайной величины и дисперсии непрерывной случайной величины имеем
М(Х)= 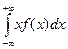 =
= 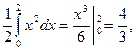
D(Х)= 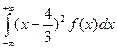 =
= 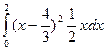 =
= 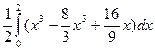 =
= 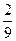
и, наконец, s(Х) = 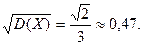
Остальные вопросы задания решаются самостоятельно.
ЗАНЯТИЕ 13
ЛОГИКА И ТЕОРИЯ ГРАФОВ
Содержание:
Задание 26 (по теории графов).
Задание 27 (по логике).
Задание 26 (по теории графов). Пусть граф G задан матрицей смежности А.
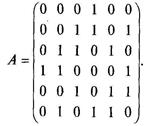
Построить диаграмму этого графа, если
Решение. Диаграмму графа, имеющего шесть вершин, представим на рис. 2.19.
Любой ориентированный граф является бинарным отношением А под V, где V— множество вершин графа, а пары из X— ребра.
Для конечного числа V вершин отношение X можно представить тремя способами:
графически, т.е. диаграммой (рис. 2.19);
с помощью таблиц, в которых представлены 1 и 0;
с помощью матриц (в случае матриц смежности).
Такая форма записи отношений удобна при решении многих логических и производственных задач. Она также используется при машинной обработке для систематизации информации
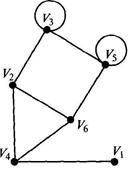 |
| Рис. 2.19. Граф к заданию 23. |
Задание 27 (по логике).
Составить таблицу истинности логической операции.
(х1Ùх2)Ú ( 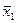 Ú
Ú 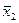 )
)
Решение. Последовательность действий представлена в следующей таблице:
Таблица
| х1 | х2 | х1Ùх2 | х1 | х2 | 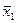 | 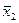 | 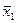 Ú Ú 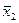 | х1Ùх2 | 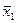 Ú Ú 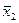 | (х1Ùх2)Ú( 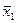 Ú Ú 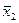 ) ) | ||
Ответ дан в заштрихованном столбце.
