Тема 8. Дифференциальные уравнения
Основные понятия
1. Общим решениемдифференциального уравненияпервого порядка называется дифференцируемая функция y=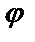 
(х,С), которая при любом значении произвольной постоянной С является решением данного уравнения. Решения, получающиеся из общего решения y= 
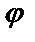(х,С) при определенном значении произвольной постоянной С, называются частными. Задача нахождения частного решения, удовлетворяющего начальным условиям y= 
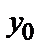при 
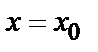(другая запись 
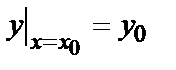), называется задачей Коши.
График всякого решения y=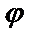 
(х) данного дифференциального уравнения, построенный на плоскости хОy, называется интегральной кривой этого уравнения.
8.2. Дифференциальные уравнения с разделяющимися переменными.Наиболее простым дифференциальным уравнением первого порядка является уравнение вида:
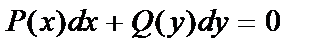, (1)
где P(x) зависит только от х, а Q(y) - от у.
Проинтегрировав почленно это уравнение, получаем:
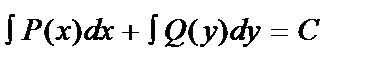- его общий интеграл.
8.3. Однородные дифференциальные уравненияпервого порядка приводятся к уравнению с разделяющимися переменными.
Функция f (x; y) называется однородной функцией n-го порядка (измерения), если при умножении каждого ее аргумента на произвольный множитель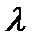 
вся функция умножится на 
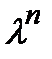, то есть: 
.
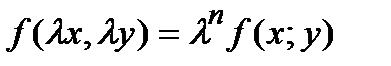Например,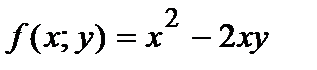 
- однородная функция второго порядка, так как 
.
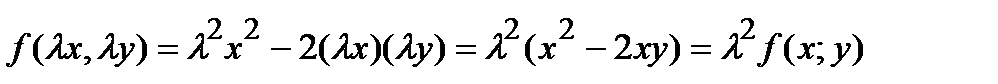Дифференциальное уравнение
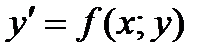(2)
называется однородным, если функция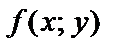 
однородного нулевого порядка.
Если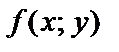 
однородная функция нулевого порядка, то по определению 
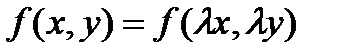. Положив 
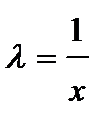, получаем: 
.
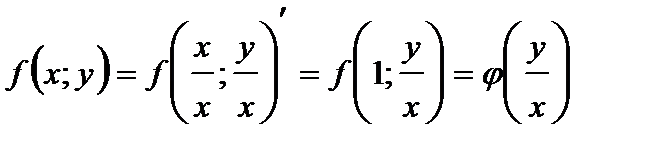Дифференциальное уравнение (2) можно записать в виде:
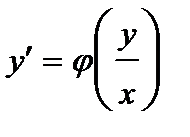(3)
Однородное дифференциальное уравнение (3) преобразуется в уравнение с разделяющимися переменными при помощи замены переменной (подстановк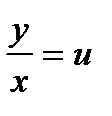и): 
или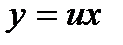 
.
Подставив 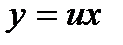и 
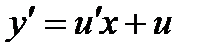в уравнение (3) получаем:
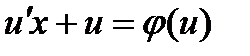или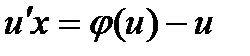 
,
то есть уравнение с разделяющимися переменными. Найдя его общее решение (общий интеграл), следует заменить в нем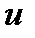 
на 
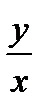. Получим общее решение (интеграл) исходного уравнения.
8.4. Линейные дифференциальные уравнения.Дифференциальное уравнение первого порядка называется линейным, если оно имеет вид:
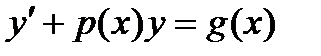(4)
где 
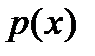и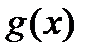 
- некоторые (непрерывные) функции переменной х. В случае, когда 
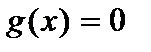, уравнение называетсяоднородным; если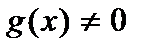 
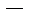неоднородным.
Общее решение дифференциального уравнения (4) будем искать в виде: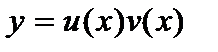 
. Так как 
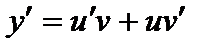, то подставив в уравнение (4), получим:
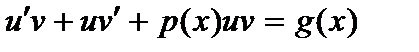или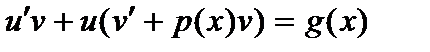 
.
Сначала находят частное решение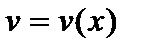 
уравнения 
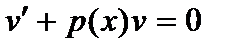, тогда функция 
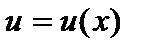- решение уравнения 
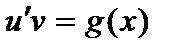. Учитывая, что 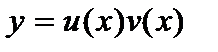, получим общее решение линейного дифференциального уравнения (4).
8.5. Дифференциальное уравнение n–го порядка, разрешенное относительно производной, имеет вид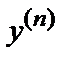 
=f(х, у, у′,…, 
).
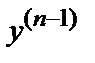Задача нахождения решения у=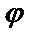 
(х) данного уравнения, удовлетворяющего начальным условиям 
; 
; 
; … ; 
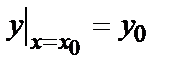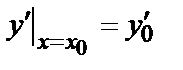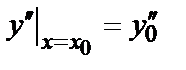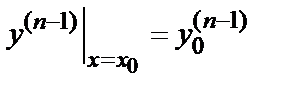, называется задачей Коши.
Для нахождения частного решения иногда используют так называемые краевые условия. Эти условия (их число не должно превышать порядка уравнения) задаются не в одной точке, а на концах некоторого промежутка. Краевые условия ставятся лишь для уравнений порядка выше первого.
Теорема существования и единственности решения задачи Коши.Если в уравнении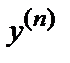 
=f(х, у, у′, … , 
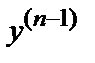) функция f(х, у, у′,…, ):
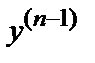a) непрерывна по всем своим аргументам х, у, у′, … , 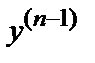в некоторой области D их изменения;
б) имеет ограниченные в области D частные производные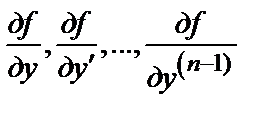 
по аргументам у, у′, … 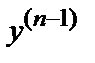, то найдется интервал 
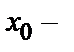h< х < 
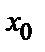+h (h >0), на котором существует единственное решение у= 
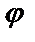(х) данного уравнения, удовлетворяющее условиям 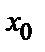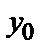у( )= 
; у′( )=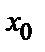 
; … ; 
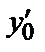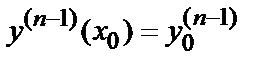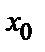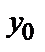, где значения х= ; у= 
; у′=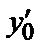 
; … ; 
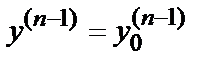содержатся в области D.
Проинтегрировать ( в конечном виде ) уравнение n–го порядка можно только в некоторых частных случаях.
8.6. Линейное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид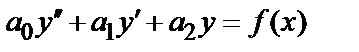 
, где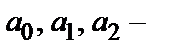 
числа, причем 
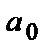≠0. Если f(х)=0, то уравнение называется однородным, а если f(х)≠ 0–неоднородным.
Квадратное уравнение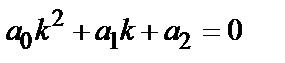 
называется характеристическим уравнением дифференциального уравнения 
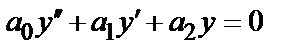. Пусть D= 
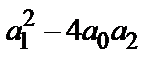дискриминант квадратного уравнения. Возможны следующие случаи:
1) D>0 – общим решением уравнения 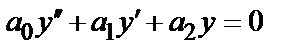является функция 
( 
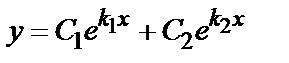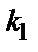и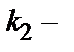 
корни характеристического уравнения);
2) D=0 – общим решением служит функция у=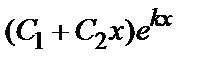 
(k–корень характеристического уравнения);
3) D<0–общим решением является функция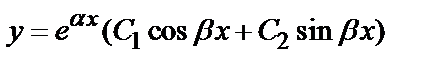 
( 
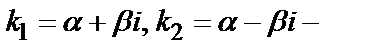корни характеристического уравнения).
Решение линейного неоднородного дифференциального уравнения второго порядка с постоянными коэффициентами основывается на следующей теореме .
Теорема.Если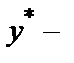 
некоторое частное решение неоднородного уравнения 
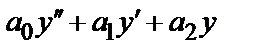=f(х)и Y–общее решение соответствующего однородного уравнения 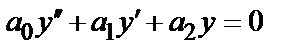, то общее решение неоднородного уравнения имеет вид у=Y+у*.
Укажем правило нахождения частного решения неоднородного уравнения методом неопределенных коэффициентов.
1) Пусть f(х)=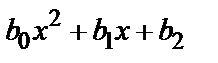 
; тогда:
а) у*=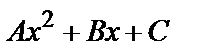 
, если нуль не является корнем характеристического уравнения;
б) у*=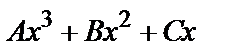 
, если нуль является простым корнем характеристического уравнения;
в) у*=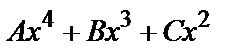 
, если нуль является двукратным корнем характеристического уравнения.
2) Пусть f(х)=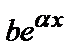 
; тогда:
а) у*=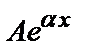 
, если число 
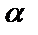не является корнем характеристического уравнения;
б) у*=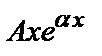 
, если число 
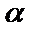является корнем характеристического уравнения;
в) у*=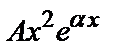 
, если число 
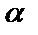является двукратным корнем характеристического уравнения.
3) Пусть f(х)=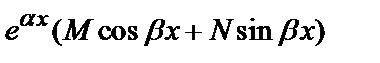 
; тогда:
а) у*=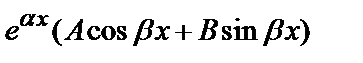 
, если число 
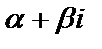не является корнем характеристического уравнения;
б) у*=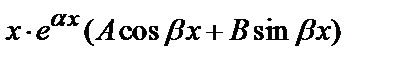 
, если число 
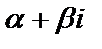является корнем характеристического уравнения.
8.7. Решение типового задания
Пример 1. Найти общее решение уравнения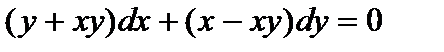 
.
Решение. Выносим общий множитель из первой и второй скобки:
.
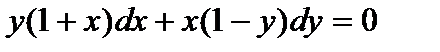Получаем уравнение с разделяющимися переменными, разделив его на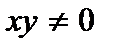 
, получим
.
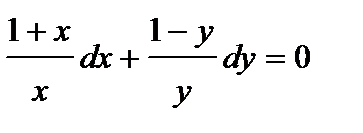Интегрируя последнее уравнение, получаем:
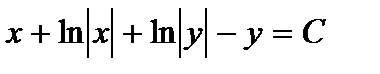или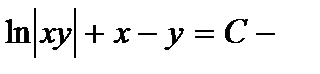 
общий интеграл
Пример 2. Найти общее решение уравнения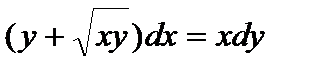 
.
Решение. Функции P и Q – однородные функции первого порядка.
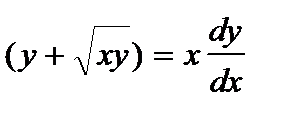или 
.
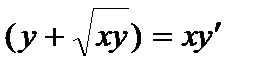Положим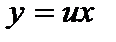 
, тогда 
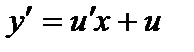. Подставляя в последнее уравнение, получаем:
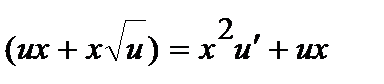или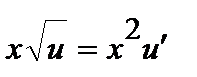 
.
Учитывая, что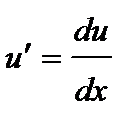 
, получаем 
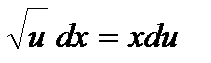или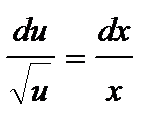 
.Интегрируя почленно это уравнение, имеем:
.
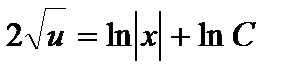Возвращаясь к старой переменной, получаем общее решение:
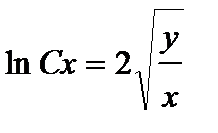или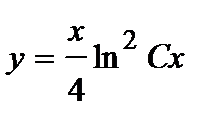 
.
Пример 3.Найти общее решение уравнения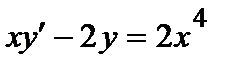 
.
Решение.Разделив левую и правую части на х, приходим к линейному неоднородному уравнению:
.
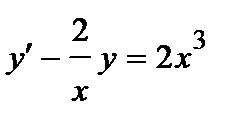Пусть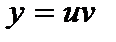 
, тогда 
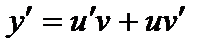. Подставляя в последнее уравнение, получаем:
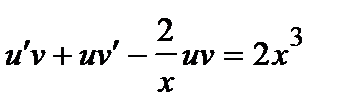или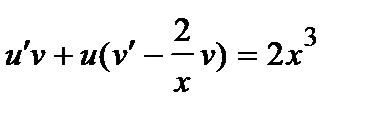 
.
Положим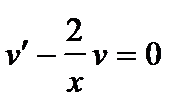 
или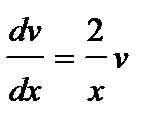 
, откуда 
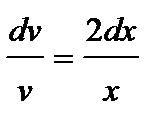. Проинтегрировав, найдем какое-либо частное решение этого уравнения, например, при С=0 имеем 
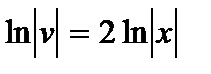и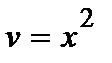 
.
Найденное значение 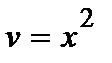подставляем в уравнение 
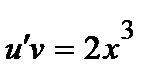или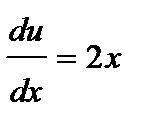 
.
Решая это уравнение с разделяющимися переменными, получаем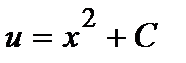 
. Тогда окончательно имеем 
.
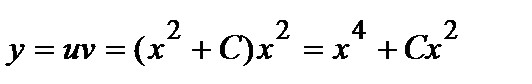Пример 4. Найти общее решение уравнения 2ху′′′=у′′ и частное решение, удовлетворяющее начальным условиям у(1)=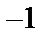 
; у′(1)=0; у′′(1)=1.
Решение. Пусть у′′=z. Имеем 2хz′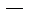 
z=0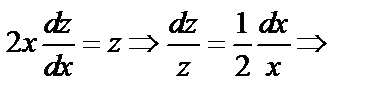 
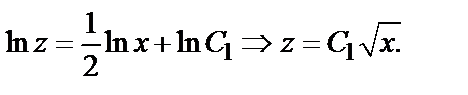
Но z=у′′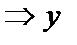 
′′= 
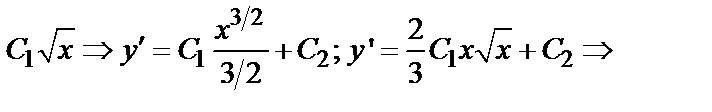
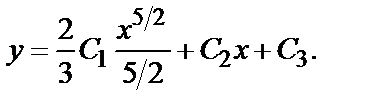Следовательно, у= 
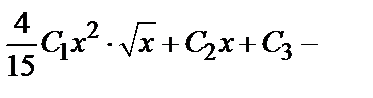общее решение дифференциального уравнения.
Чтобы найти частное решение, подставим в выражения для у, у′ и у′′ значение х=1:
;
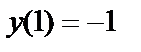
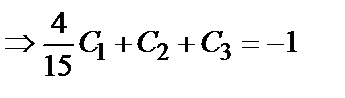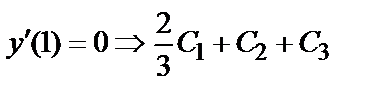=0;
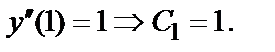
Из системы уравнений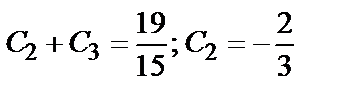 
находим 
; 
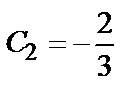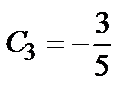. Значит, искомое частное решение имеет вид:
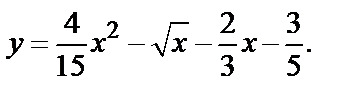
Пример 5. Найти общее решение уравнения y′′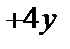 
′+13у=5sin2х и частное решение, удовлетворяющее начальным условиям 
= 
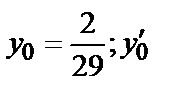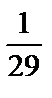при х=0.
Решение. Рассмотрим однородное уравнение y′′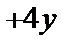 
′+13у=0. Соответствующее характеристическое уравнение имеет вид 
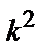+4k+13=0, откуда 
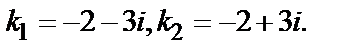Следовательно, Y=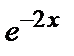 
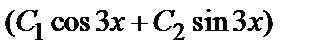общее решение однородного уравнения.
Частное решение неоднородного уравнения будем искать в виде
у*=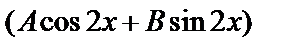 
. Имеем:
(у*)′=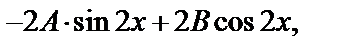 
(у*)′′= 
.
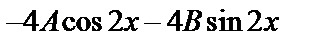Подставим эти выражения в неоднородное уравнение
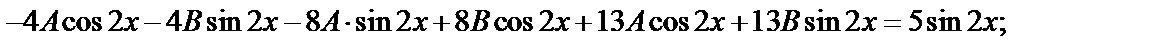
(9А+8В)cos2х+(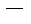 
8А+9В)sin2х=5sin2х
и получим систему для вычисления коэффициентов А и В:
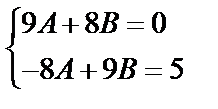
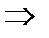
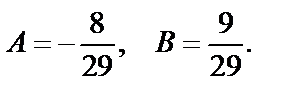
Итак, частное решение неоднородного уравнения имеет вид:
у*=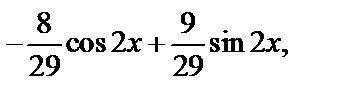 
а общее решение неоднородного уравнения – вид
у=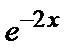 
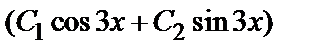
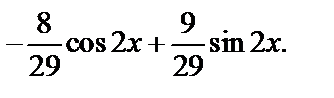
Найдем частное решение, удовлетворяющее заданным начальным условиям:
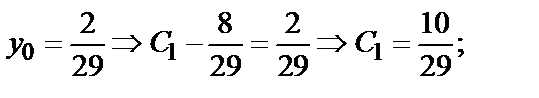
y=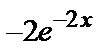 
+ 
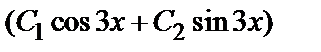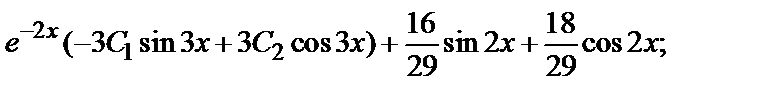
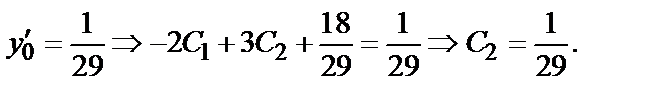
Искомое частное решение таково:
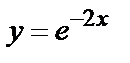
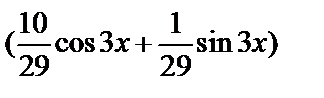
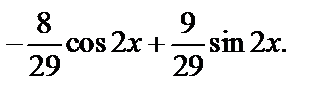
Задачи 361-390:
Найти общее решение дифференциальных уравнений.
361. а) 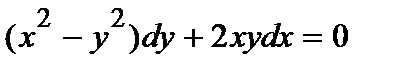 | б)  |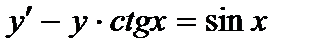
362. а) 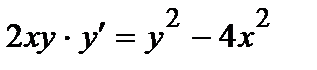 | б)  |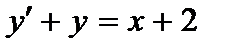
363. а) 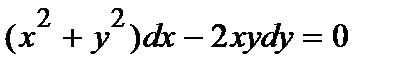 | б)  |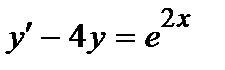
364. а) 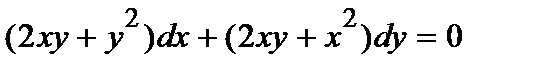 | б)  |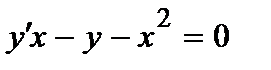
365. а) 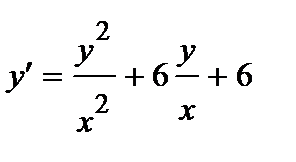 | б)  |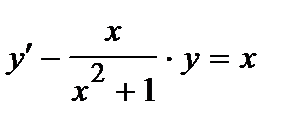
366. а) 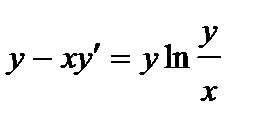 | б)  |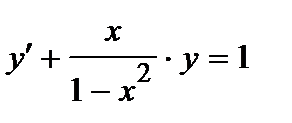
367. а) 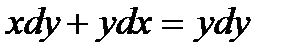 | б)  |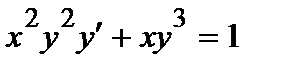
368. а) 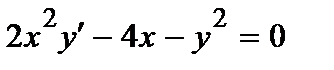 | б)  |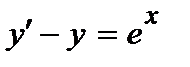
369. а) 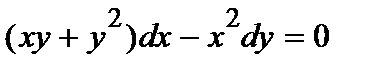 | б)  |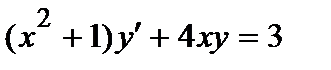
370. а) 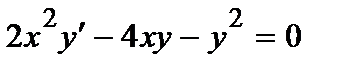 | б)  |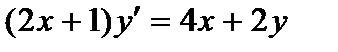
371. а) 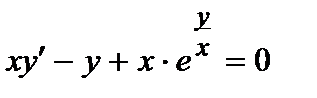 | б)  |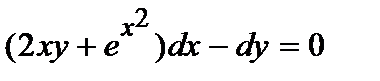
372. а) 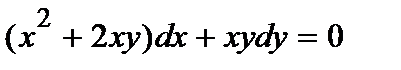 | б)  |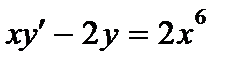
373. а) 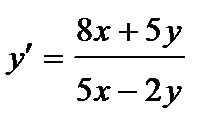 | б)  |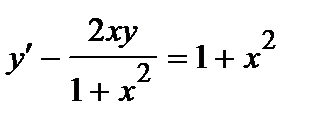
374. а) 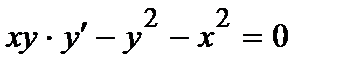 | б)  |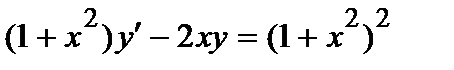
375. а) 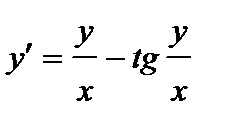 | б)  |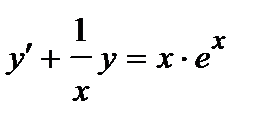
376. а) 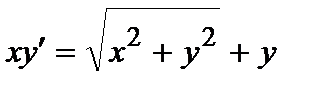 | б)  |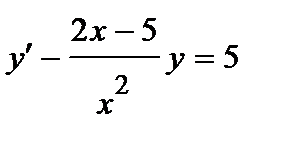
377. а) 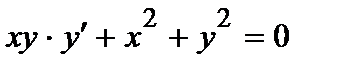 | б)  |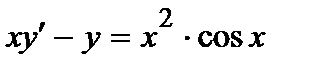
378. а) 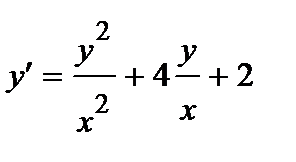 | б)  |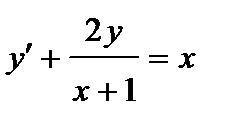
379. а) 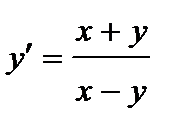 | б)  |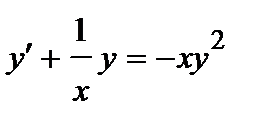
380. а) 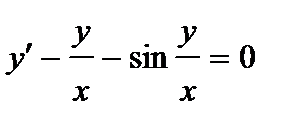 | б)  |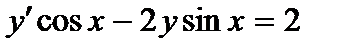
381. a) 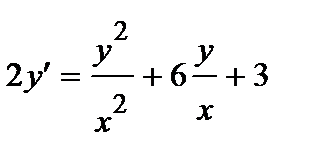 | б)  |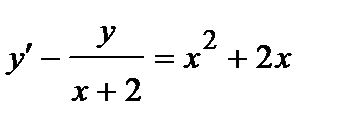
382. a) 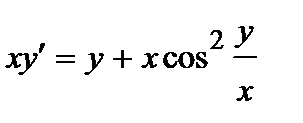 | б)  |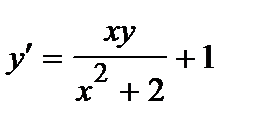
383. a) 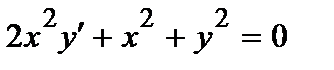 | б)  |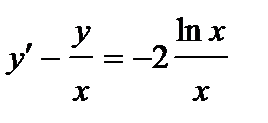
384. a) 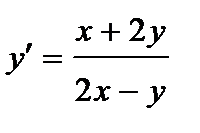 | б)  |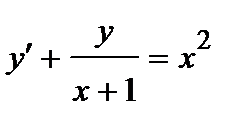
385. a) 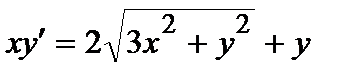 | б)  |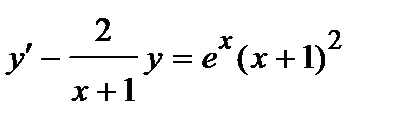
386. a) 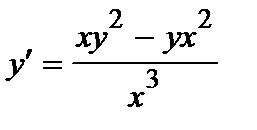 | б)  |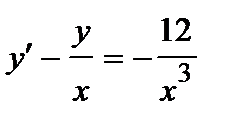
387. a) 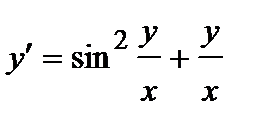 | б)  |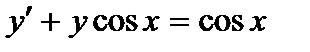
388. a) 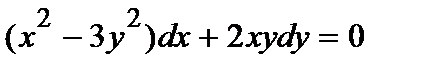 | б)  |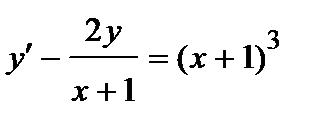
389. a) 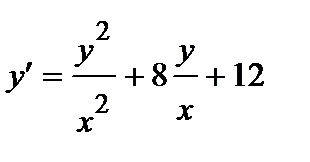 | б)  |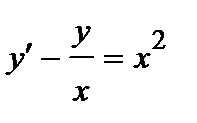
390. a) 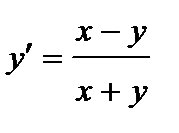 | б)  |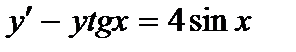
Задачи №391-420:
Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее начальным условиям.
391. 
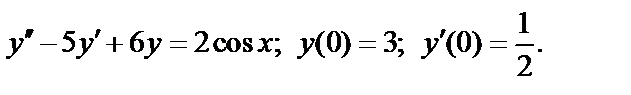
392. 
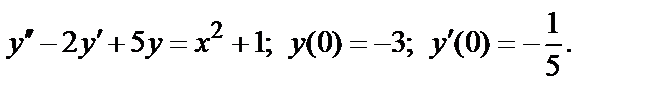
393. 
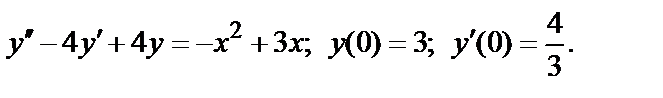
394. 
395. 
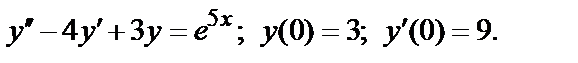
396. 
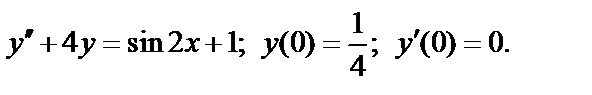
397. 
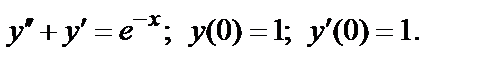
398. 
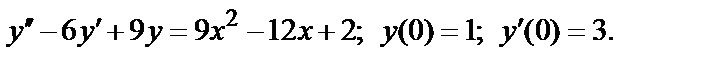
399. 
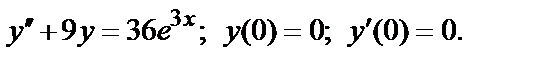
400. 
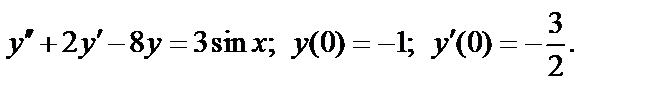
401. 
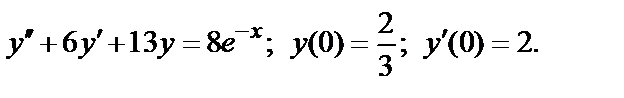
402. 
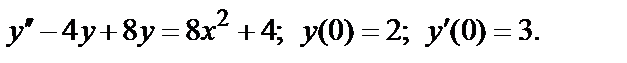
403. 
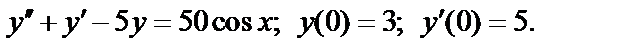
404. 
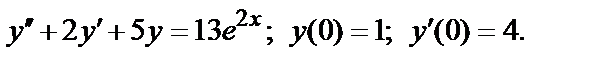
405. 
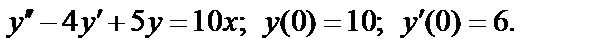
406. 
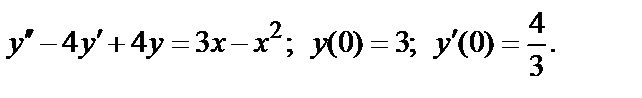
407. 
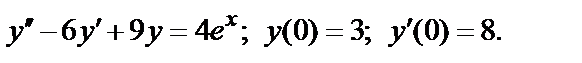
408. 
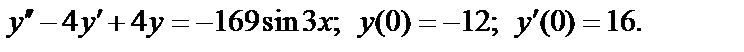
409. 
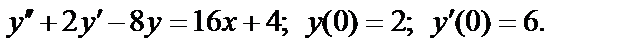
410. 
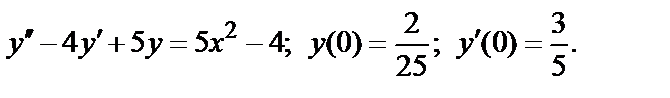
411. 
; 
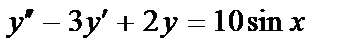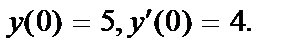
412. 
; 
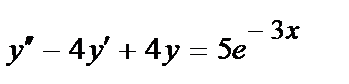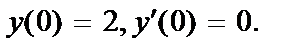
413. 
; 
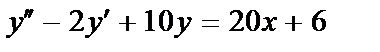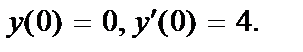
414. 
; 
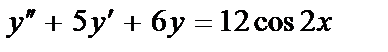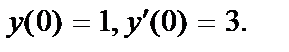
415. 
; 
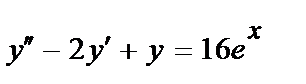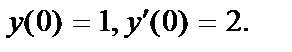
416. 23.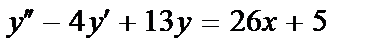 
; 
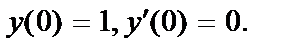
417. 
; 
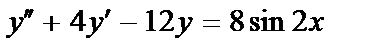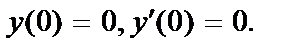
418. 
; 
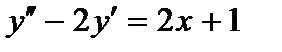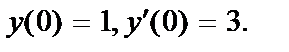
419. 
; 
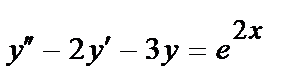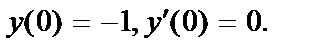
420. 
; 
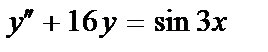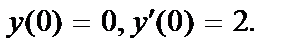
Тема 9. Ряды
Числовой ряд. Основные понятия
Числовой ряд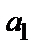 
+ 
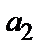+…+а 
+… = 
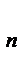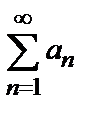, (1)
называется сходящимися, если существует предел его частичных сумм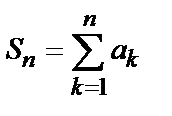 
. Число 
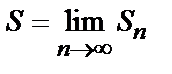называется суммой ряда. Если же предел частичных сумм не существует, то ряд (1) называется расходящимися.
Необходимый признак сходимости: если ряд (1) сходится, то его общий член стремится к нулю при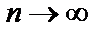 
: 
.
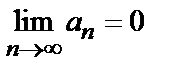К достаточным признакам сходимости рядов с положительными членами (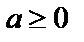 
) относятся:
9.2. Признак сравнения в предельной форме: если
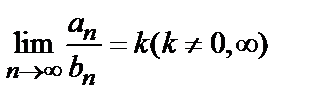, (2)
то ряды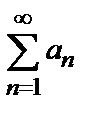 
и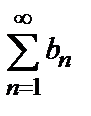 
одновременно сходится или расходится. В качестве эталонных рядов для сравнения обычно служат:
ряд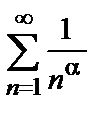 
сходящийся при 
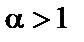и расходящийся при 
;
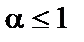ряд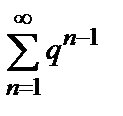 
, сходящийся при 
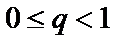и расходящийся 
.
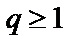9.3. Признак Даламбера: если существует
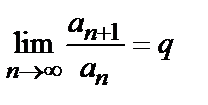, (3)
то ряд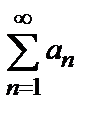 
сходится при 
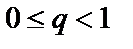и расходится при 
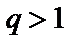. Если же 
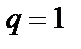, то вопрос о сходимости ряда этим признаком не решается.
Ряд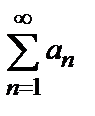 
с членами, имеющими разные знаки, называется условно сходящимся, если ряд 
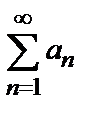сходится, а ряд 
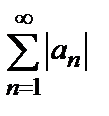расходится, и абсолютно сходящимся, если ряд 
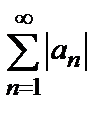сходится.
9.4. Радикальный признак Коши: если для ряда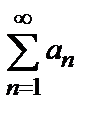 
существует
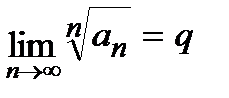, (4)
то ряд сходится при 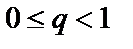и расходится при 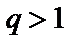. Если же 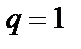, то вопрос о сходимости ряда этим признаком не решается.
9.5. Признак Лейбница: если члены ряда 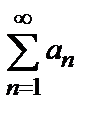удовлетворяют условиям:
1) 
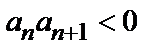(т.е. ряд знакочередующийся);
2) 
;
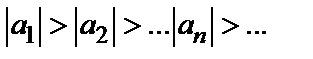3) 
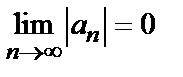, то ряд сходится. Погрешность 
, происходящая от замены суммы сходящегося знакочередующегося ряда суммой его первых n членов, по абсолютной величине меньше первого из отброшенных членов:
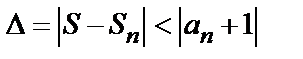. (5)
9.6. Степенной ряд.Ряд вида
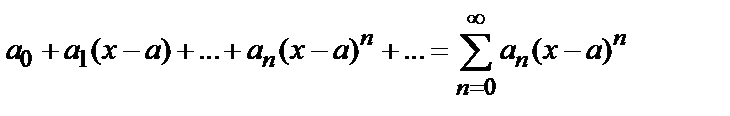(6)
называется степенным рядом [относительно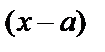 
], точка 
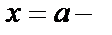центром разложения, 
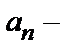коэффициентами ряда. Число 
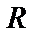называется радиусом сходимостистепенного ряда, если ряд (6) сходится при 
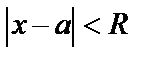и расходится 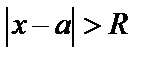при 
. При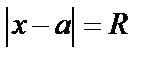 
ряд может как сходится, так и расходится. Интервал 
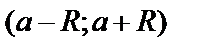называется интервалом сходимости степенного ряда (6). Радиус сходимости R может быть найден по формуле
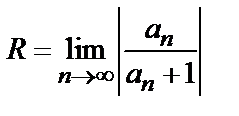. (7)
Степенной ряд (6) внутри интервала сходимости можно почленно дифференцировать и интегрировать с сохранением радиуса сходимости.
9.7. Решение типового задания
Пример 1. Исследовать на сходимость числовой ряд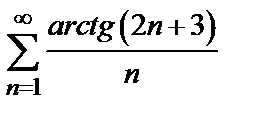 
.
Решение. Проверяем сходимость ряда по признаку Даламбера (3). Так как общий член ряда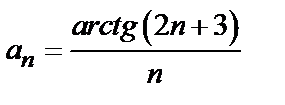 
, то, заменяя в выражении n-го члена n на n+1, находим 
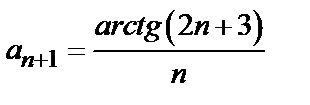. Затем ищем предел отношения последующего члена 
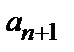к предыдущему 
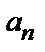при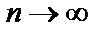 
:
.
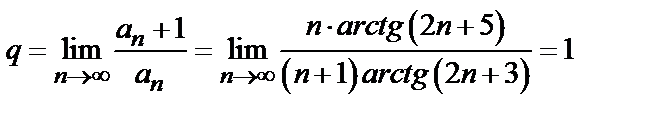Поскольку полученный предел равен единице, признак Даламбера не дает ответа на вопрос о сходимости ряда (здесь для вычисления предела было использовано правило Лопиталя). Применим теперь признак сравнения в предельной форме. В качестве эталонного ряда выберем ряд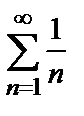 
, 
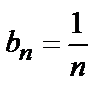и в силу формулы (2) получим
.
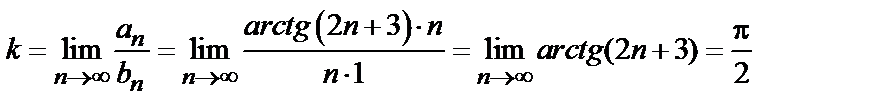Следовательно, исследуемый ряд является расходящимся, так как эталонный ряд с общим членом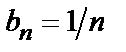 
расходится (гармонический ряд).
Пример 2. Исследовать на сходимость числовой ряд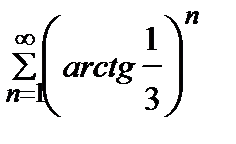 
.
Решение. Проверяем сходимость ряда по радикальному признаку Коши (4).
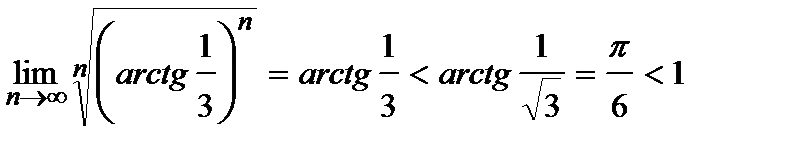
– ряд сходится.
Пример 3.Исследовать на сходимость числовой ряд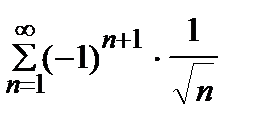 
.
Решение. Проверяем сходимость ряда по признаку Лейбница (4).
1) 
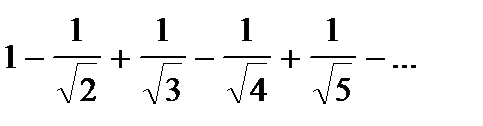(т.е. ряд знакочередующийся);
2) 
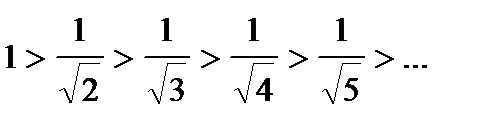(монотонно убывают);
3) 
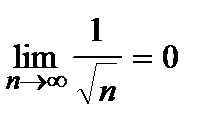, то ряд сходится.
Ряд из абсолютных величин членов ряда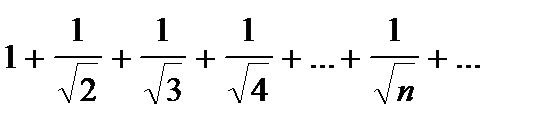 
, общий член которого имеет вид 
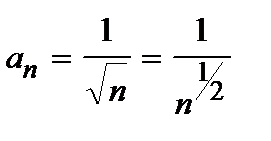. Обобщенный гармонический ряд 
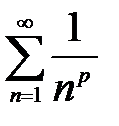при p<1 расходится. Таким образом, исследуемый ряд сходится условно.
Пример 4. Найти радиус и интервал сходимости степенного ряда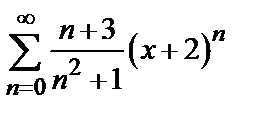 
. Исследовать сходимость ряда на концах интервала сходимости.
Решение. Радиус сходимости находим по формуле (7):
,
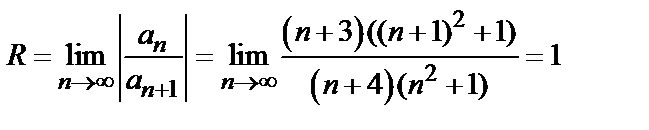Интервал сходимости данного ряда определяется интервалом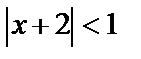 
или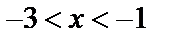 
.
Исследуем концы интервала сходимости. При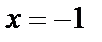 
получаем числовой ряд
,
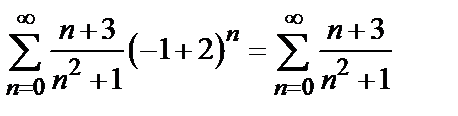расходимость которого может быть установлена с помощью предельного признака сравнения (эталонный ряд – гармонический).
При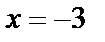 
получаем числовой ряд
,
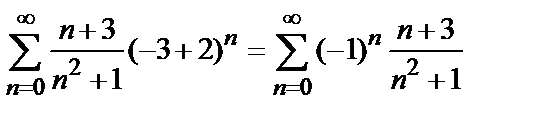который сходится по признаку Лейбница. Так как ряд, составленный из абсолютных членов данного ряда, т.е. ряд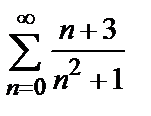 
, расходится, то исследуемый ряд сходится условно.
Таким образом, интервал сходимости исследуемого степенного ряда имеет вид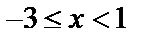 
.
Задачи №421-450:
Исследовать сходимость рядов:
а) по признаку Даламбера;
б) по радикальному признаку Коши.
421. а) 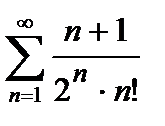 | б)  |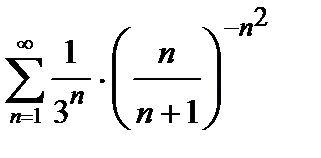
422. а) 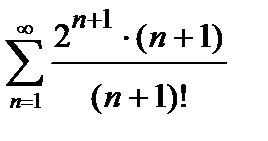 | б)  |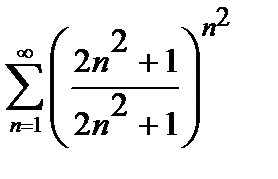
423. а) 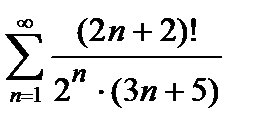 | б)  |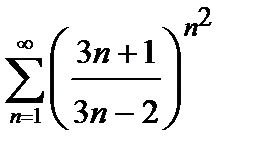
424. а) 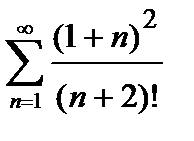 | б)  |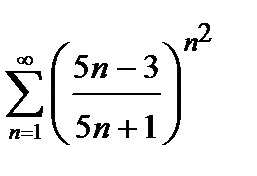
425. а) 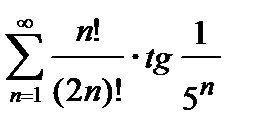 | б)  |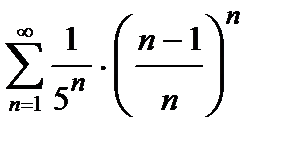
426. а) 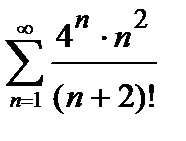 | б)  |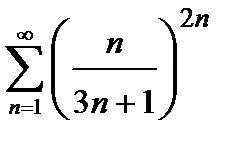
427. а) 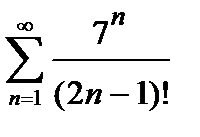 | б)  |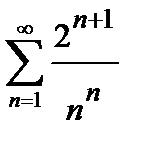
428. а) 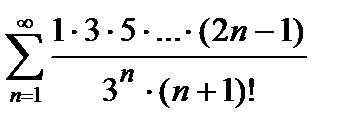 | б)  |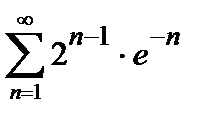
429. а) 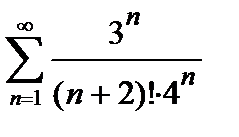 | б)  |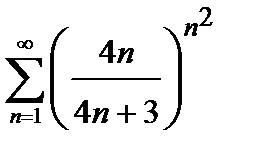
430. а) 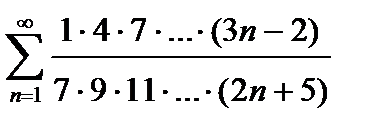 | б)  |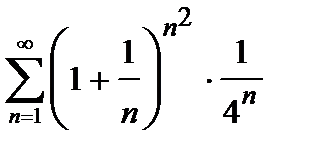
431. а) 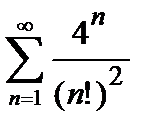 | б)  |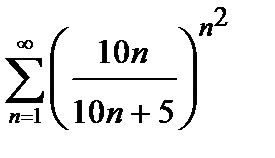
432. а) 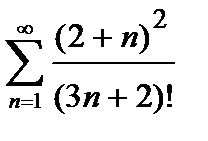 | б)  |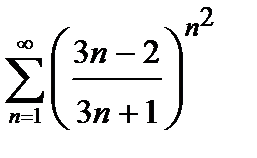
433. а) 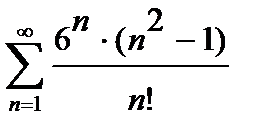 | б)  |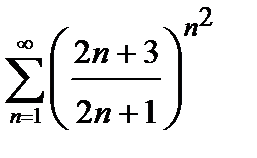
434. а) 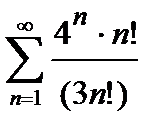 | б)  |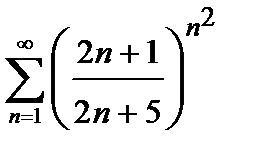
435. а) 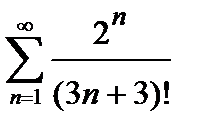 | б)  |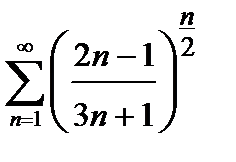
436. а) 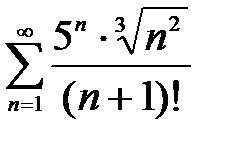 | б)  |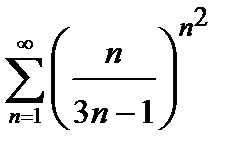
437. а) 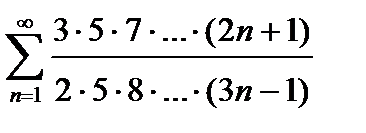 | б)  |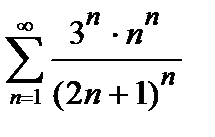
438. а) 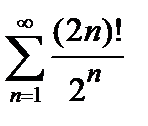 | б)  |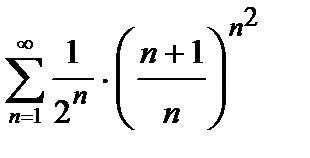
439. а) 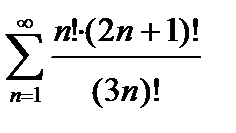 | б)  |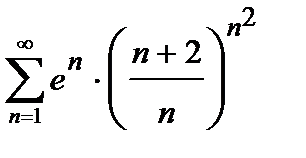
440. а) 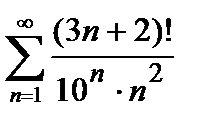 | б)  |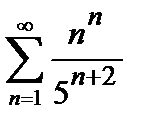
441. а) 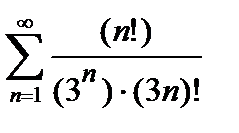 | б)  |
442. а) 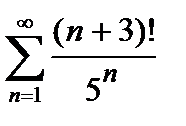 | б)  |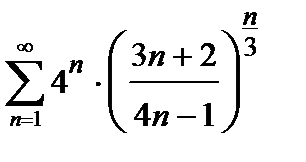
443. а) 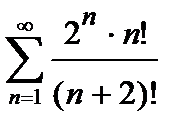 | б)  |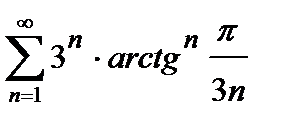
444. а) 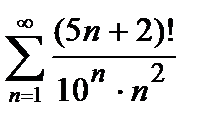 | б)  |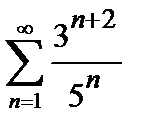
445. а) 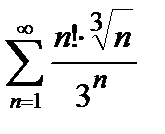 | б)  |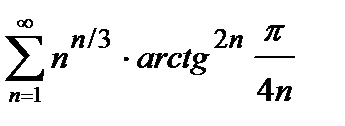
446. а) 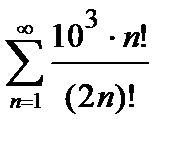 | б)  |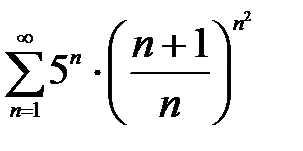
447. а) 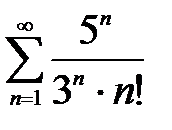 | б)  |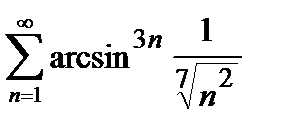
448. а) 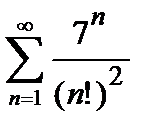 | б)  |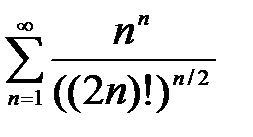
449. а) 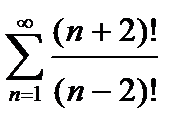 | б)  |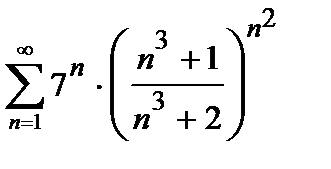
450. а) 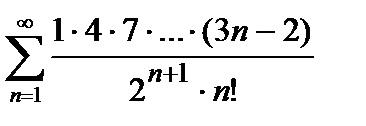 | б)  |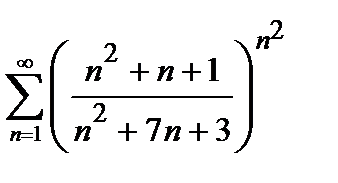
Задачи №451-480:
Исследовать на абсолютную и условную сходимость знакочередующиеся ряды:
| 451. |