Дифференциальные уравнения I порядка. Обыкновенные дифференциальные уравнения (ОДУ)

Обыкновенные дифференциальные уравнения (ОДУ)

Дифференциальным уравнением называется соотношение, связывающее между собой независимую переменную x, искомую функцию y(x) и ее производные различных порядков по x. Порядок старшей производной, входящей в данное уравнение, называется порядком этого уравнения. В общем виде дифференциальное уравнение порядка n имеет вид

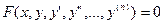. (1)

В уравнении (1) могут отсутствовать x, y или отдельные производные порядка ниже n.

Всякая функция 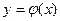, при подстановке которой в (1) получается верное равенство, называется решением этого дифференциального уравнения.

Решить или проинтегрировать дифференциальное уравнение – значит найти все его решения в заданной области. Всякое дифференциальное уравнение имеет бесконечно много решений. График решения дифференциального уравнения называется интегральной кривой.

Общим решением дифференциального уравнения (1) называется его решение 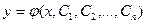, содержащее столько произвольных постоянных, каков порядок этого уравнения. Если общее решение задано в неявном виде 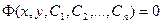, то его называют общим интегралом.

Всякое решение дифференциального уравнения, которое получается из общего решения приданием определенных значений произвольным постоянным, в него входящим, называется частным решением этого дифференциального уравнения.

Дифференциальное уравнение I порядка имеет вид

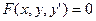. (2)

В простейших случаях его можно разрешить относительно производной и представить в виде

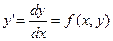. (3)

Поскольку геометрический смысл производной в точке – тангенс угла наклона касательной, проведенной к интегральной кривой в этой точке, а угол определяет направление, то для дифференциального уравнения (3) говорят о поле направлений, заданном в области определения функции .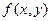

Если требуется найти решение дифференциального уравнения (2), удовлетворяющее заданному начальному условию 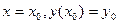, то говорят о задаче Коши.

Теорема. Пусть в дифференциальном уравнении (3) функция 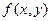и ее частная производная 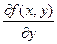непрерывны на множестве D плоскости Oxy. Тогда для всякой точки 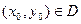найдется решение 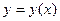уравнения (3), удовлетворяющее начальному условию 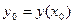. При этом если два решения уравнения (3) 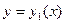и 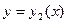совпадают хотя бы для одной точки 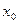, т.е. 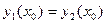, то они совпадают для всех значений аргумента из их областей определения.

Приведенная теорема устанавливает условия существования и единственности решения задачи Коши для дифференциальных уравнений I порядка.

Не существует общего метода интегрирования дифференциальных уравнений I порядка.

Дифференциальные уравнения I порядка