Производная по направлению и градиент

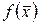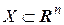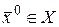Пусть функция определена на открытом множестве и . Рассмотрим прямую 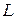: 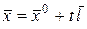, где 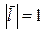. Здесь 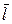– направляющий вектор прямой (рис.1). В координатном виде уравнения кривой записать следующим образом:

…. .

	Рис.1

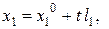
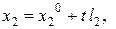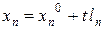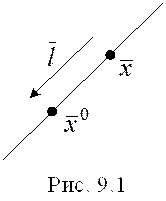
Здесь вектор 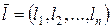единичный вектор, проходящий через точку .

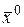Определение 18. Производной по направлению вектора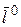(прямой 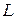) в точке 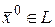называют предел по множеству .

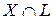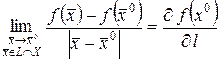(18)

Если 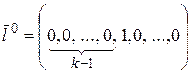, то совпадает с направлением оси 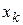и производная по направлению 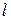совпадает с частной производной .

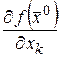Запишем (18) подробнее. Так как 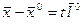, , 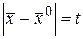то

.

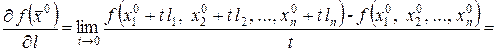
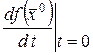По теореме о дифференцировании сложной функции имеем

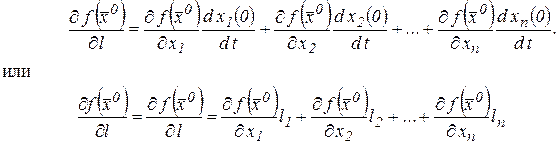(19)

В частном случае, в пространстве 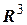, формула (19) для функции 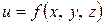в точке 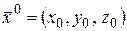по направлению 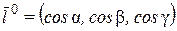, формула имеет вид

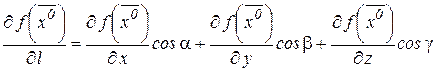. (20)

Определение 19. Градиентом дифференцируемой в точке 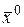функции 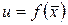называется n – мерный вектор

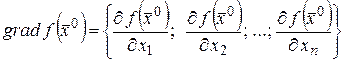. (21)

В пространстве 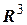формула (21) имеет вид :

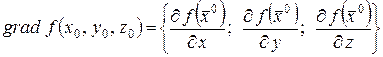
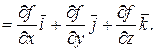
На плоскости Oxy :

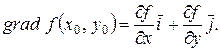
С помощью символического оператора 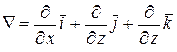, который называется оператором Гамильтона, градиент в R³ также обозначают

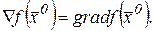
Используя понятие градиента можно в векторной форме записать формулу полного приращения функции в точке :

,

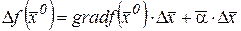а также дифференциал функции

,

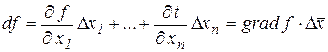и производную функции по направлению

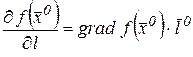, (22)

где 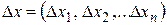– вектор приращений аргумента, 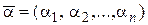- вектор бесконечно малых.

Свойства градиента:

1. Если вектор градиент функции 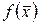тождественно равен нулю для любого 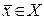, то функция 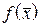постоянна на множестве Х.

2. Есл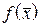и и 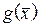– дифференцируемые функции в 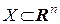, то справедливы следующие соотношения

а) ;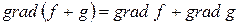

б) ;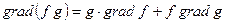

в) ,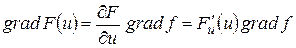

где 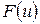дифференцируемая функция одной переменной .

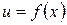Справедливость этих свойств следует из определения градиента и свойств векторов.

3. Производная функции 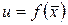по направлению вектора 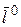(рис.2) принимает наибольшее значение в направлении 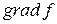и равна модулю 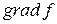, т.е.

.

Рис.2

ƒ Из (22) следует .

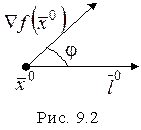
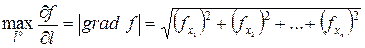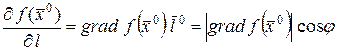Так как 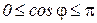, то . <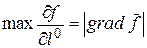

Таким образом, 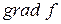есть вектор, указывающий направление наибольшего возрастания функции в данной точке и имеющий модуль, равный скорости этого возрастания.

4. Пусть 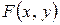дифференцируемая функция, и

( )

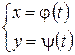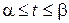параметрические уравнения некоторой гладкой кривой Г, удовлетворяющие условию

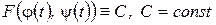. (23)

Такая кривая называется линией уровня функции .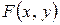

Вектор 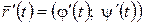(рис 7.3) является касательным вектором к кривой Г, а 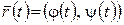– радиусом-вектором точки М .

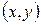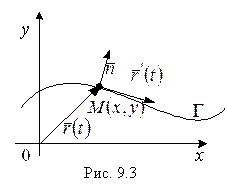Продифференцируем (23) по t как сложную функцию:

,

.

Рис.3

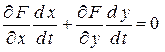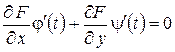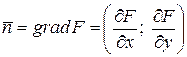Обозначим . Тогда в векторном виде будем иметь

,

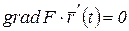т.е. скалярное произведение двух векторов рано нулю. Это означает, что в каждой точке линии уровня векторы 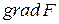и 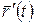, т.е. вектор градиент и касательный вектор к кривой ортогональны, или вектор градиент в каждой точке ортогонален линии уровня.

Примеры. 1) Найти наибольшее значение 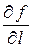в точке 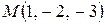, если .

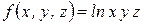Решение. Найдем 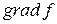в точке М:

; .

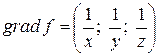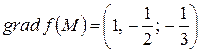Тогда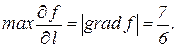

2) Найти производную функции 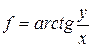в точке 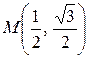по направлению внешней нормали к окружности 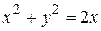в точке .

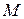Решение.Производная по направлению вычисляется, как скалярное произведение 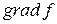и вектора направления 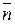(внешняя нормаль)

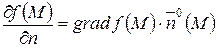
Вычислим 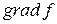в точке М:

,

.

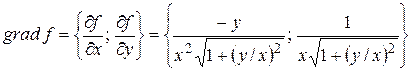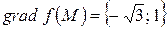Вычислим вектор 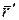в точке М. Для этого в уравнении окружности 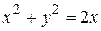определим зависимость х и у от параметра 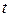: 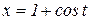, 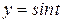. Так как точка М принадлежит окружности, получаем

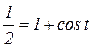и .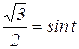

Отсюда . .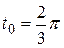

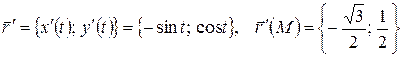Поскольку векторы 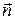и 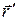ортогональны, то координаты вектора нормали находятся из соотношения

.

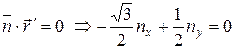Отсюда получаем, 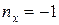, 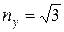. Нормируем вектор :

,

.

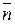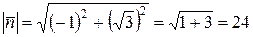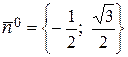Производная по направлению нормали к окружности в точке М равна

.
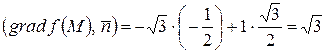