Криволинейный интеграл 1-го рода.

1. Длина кривой.

Если подынтегральная функция f(x, y, z) ≡ 1, то из определения криволинейного интеграла 1-го рода получаем, что в этом случае он равен длине кривой, по которой ведется интегрирование:

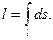(14.14)

1. Масса кривой.

Считая, что подынтегральная функция γ (x, y, z) определяет плотность каждой точки кривой, найдем массу кривой по формуле

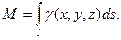(14.15)

3. Моменты кривой l найдем, рассуждая так же, как в случае плоской области: 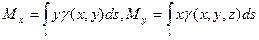- (14.16)

- статические моменты плоской кривой l относительно осей Ох и Оу;

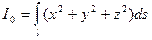- (14.17)

- момент инерции пространственной кривой относительно начала координат;

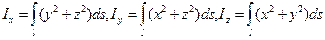- (14.18)

- моменты инерции кривой относительно координатных осей.

4.Координаты центра масс кривой вычисляются по формулам

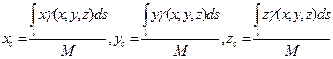. (14.19)

Билет №30. Вычисление криволинейного интеграла первого рода при различном задании области определения(дуги кривой). Свойства криволинейного интеграла первого рода.

Свойства криволинейного интеграла 1-го рода:

1. Если функция f непрерывна на кривой L, то интеграл 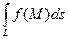существует.
2. Криволинейный интеграл 1-го рода не зависит от направления движения по кривой.

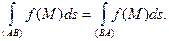(10.2)

Справедливость этих свойств следует из определения криволинейного интеграла 1-го рода.

Способ вычисления криволинейного интеграла 1-го рода.

Выберем на кривой L направление от начальной точки А и отметим, что положение точки М на кривой определяется длиной дуги АМ = s. Тогда кривую L можно задать параметрически: x = x(s), y = y(s), z = z(s), где 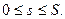Функция f(x,y,z) становится при этом сложной функцией одной переменной s: f(x(s), y(s), z(s)). Тогда интегральная сумма

,

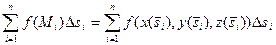где 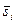- координата точки M_i, является обычной интегральной суммой для определен-ного интеграла 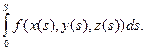Следовательно,

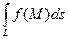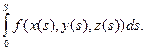= (10.3)

Если же кривая L задана в параметрической форме:

x = φ(t), y = ψ(t), z = χ(t), t₀ ≤ t ≤ T,

то, применяя в интеграле (10.3) формулу замены переменной и учитывая, что дифференциал дуги

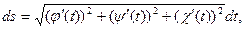
получим:

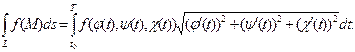(10.4)

Таким образом, вычисление криволинейного интеграла 1-го рода сводится к вычислению обычного определенного интеграла от функции переменной t в пределах, соответствующих изменению значения этой переменной на рассматриваемой кривой.

Билет№31. Криволинейный интеграл второго рода. Задача о работе силового поля .Интеграл в декартовой и векторной форме.

Вновь рассмотрим кривую L, в каждой точке которой задана функция f(M), и зададим разбиение кривой на отрезки. Выберем на каждом отрезке точку M_i и умножим значе-ние функции в этой точке не на длину i-го отрезка, как в случае криволинейного инте-грала 1-го рода, а на проекцию этого отрезка, скажем, на ось Ох, то есть на разность x_i – x_i-1 = Δx_i. Составим из полученных произведений интегральную сумму .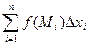

Определение 10.2. Если существует конечный предел при 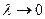интегральной суммы 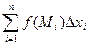, не зависящий от способа разбиения кривой на отрезки и выбора точек M_i, то от называется криволинейным интегралом второго рода от функции f(M) по кривой L и обозначается

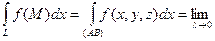
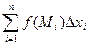. (10.5)

Подобным образом можно определить и криволинейные интегралы 2-го рода вида

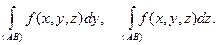
Определение 10.3. Если вдоль кривой L определены функции P(M) = P(x, y, z),

Q(M) = Q(x, y, z), R(M) = R(x, y, z) и существуют интегралы

,

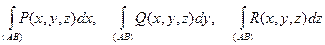то и их сумму называют криволинейным интегралом второго рода (общего вида) и полагают

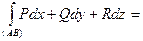
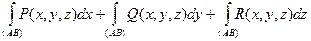. (10.6)

Замечание. Если считать, что сила 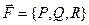действует на точку, движущуюся по кривой (АВ), то работа этой силы может быть представлена как

,

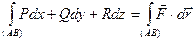то есть криволинейным интегралом 2-го рода.

Свойства криволинейного интеграла 2-го рода.

1. Если функции P(M), Q(M), R(M) непрерывны на кривой (АВ), то интеграл (10.6) существует (справедливость этого утверждения следует из определения 10.2).

1. При изменении направления кривой (то есть перемены местами начальной и конечной ее точек) криволинейный интеграл 2-го рода меняет знак:

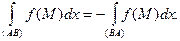(10.7)

Действительно, при этом изменяется знак Δx_i в интегральной сумме.

Способ вычисления криволинейного интеграла 2-го рода.

Теорема 10.1. Пусть кривая L задана параметрическими уравнениями

x = φ(t), y = ψ(t), z = χ(t), α ≤ t ≤ β ,

где φ, ψ, χ – непрерывно дифференцируемые функции, и на ней задана непрерывная функция f(x, y, z). Тогда интеграл (10.5) существует и имеет место равенство

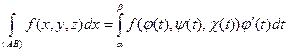. (10.8)

Доказательство.

Запишем Δx_i = x_i – x_i-1 = φ(t_i) – φ(t_i-1) и преобразуем последнюю разность по формуле Лагранжа: φ(t_i) – φ(t_i-1) = φ΄(τ_i)Δt_i, где τ_i – некоторое значение t, заключенное между t_i-1 и t_i. Выберем точку М_i так, чтобы ее координаты соответствовали значению параметра, равному τ_i : M_i(φ(τ_i), ψ(τ_i), χ(τ_i)). Подставив эти значения в формулу (10.5), получим:

.

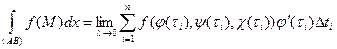Справа получен предел интегральной суммы для функции f(φ(t),ψ(t),χ(t))φ΄(t) на отрезке [α, β], равный определенному интегралу от этой функции:

,

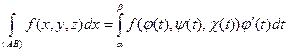что и требовалось доказать.

Следствие. Аналогичные соотношения можно получить для криволинейных интегра-лов вида 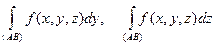, откуда следует, что

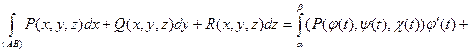
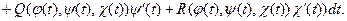(10.9)

Билет № 32. Криволинейный интеграл второго рода по замкнутому контуру. Формула Грина. Независимость криволинейного интеграла 2-го рода

От пути интегрирования.

Если в каждой точке М определенной пространственной области задано значение некоторой скалярной или векторной величины, то говорят, что задано поле этой величины (соответственно скалярноеили векторное).

Рассмотрим некоторые характеристики скалярных и векторных полей.

Определение 11.1. Если в некоторой области задано скалярное поле U(x,y,z), то поверхность, определяемая уравнением

U(x, y, z) = C, (11.1)

называется поверхностью уровня. В двумерном случае линия уровня задается уравнением U(x, y) = C. (11.1`)

Определение 11.2. Если в некоторой области задано векторное поле 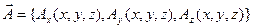, то кривая, направление которой в каждой ее точке М совпадает с направлением вектора 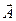в этой точке, называется векторной линией. Она задается уравнениями

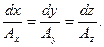(11.2)

Поверхность, составленная из векторных линий, называется векторной поверхно-стью. Если векторная поверхность образована векторными линиями, проходящими через каждую точку некоторой замкнутой кривой, то она называется векторной трубкой.

Определение 11.3. Пусть задано скалярное поле U(x, y, z). Вектор

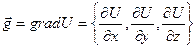(11.3)

называется градиентомвеличины U в соответствующей точке (см. лекцию 4 за 2-й семестр).

Замечание. Таким образом, скалярное поле U(x, y, z) порождает векторное поле градиента gradU.

Определение 11.4. Пусть дано векторное поле 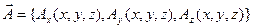. Интеграл

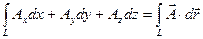(11.4)

называется линейным интегралом от вектора 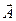вдоль кривой L. Если кривая L замкнута, то этот интеграл называют циркуляцией вектора 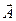вдоль кривой L.

Здесь 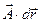- скалярное произведение векторов 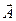и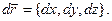

Замечание. Иногда криволинейный интеграл 2-го рода по замкнутому контуру обозначают .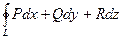

Пример. Вычислить циркуляцию векторного поля 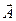={x, xy, xyz} вдоль контура L:

x² + y² = 9, z = 2 (направление обхода контура – от точки (3,0,2) к точке (0,3,2)).

Зададим контур L параметрически: x = 3cos t, y = 3sin t, z = 2 (0 ≤ t ≤ 2π). Тогда

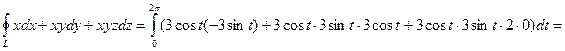
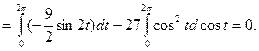
Формула Грина.

Установим связь между двойным интегралом по некоторой плоской области D и криволинейным интегралом по границе L этой области.

Пусть в плоскости Оху дана ограниченная замкнутым контуром L правильная область D. Кривые, ограничивающие эту область снизу и сверху, заданы уравнениями

y = y₁(x) и y = y₂(x), y₁(x) ≤ y₂(x), a ≤ x ≤ b (рис.1).

y

P

y=y₂(x)

M D N

y=y₁(x)

Q

O a b x

Рис. 1.

Зададим в области D непрерывные функции P(x, y) и Q(x, y), имеющие непрерывные частные производные, и рассмотрим интеграл

.

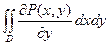Переходя к двукратному интегралу, получим:

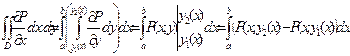(11.5)

Так как у = у₂(х) – параметрическое выражение кривой МPN, то

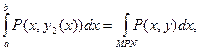
где справа стоит криволинейный интеграл по кривой MPN. Аналогично получаем, что

.

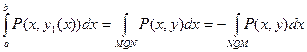Подставим полученные результаты в формулу (11.5):

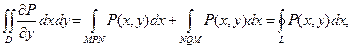(11.6)

так как контур L представляет собой объединение кривых MPN и NQM.

Так же можно получить, что 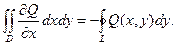(11.7)

Вычтем из равенства (11.6) равенство (11.7):

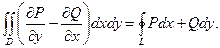
При этом обход контура L происходит по часовой стрелке. Изменим направление обхода. Тогда предыдущее равенство примет вид:

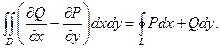(11.8)

Эта формула, задающая связь между двойным интегралом и криволинейным интегралом 2-го рода, называется формулой Грина.

Замечание 1. Если в криволинейном интеграле по замкнутому контуру не указано направление обхода, то предполагается, что он производится против часовой стрелки.

Замечание 2. Если рассматривать в плоскости Оху векторное поле {P(x,y), Q(x,y)}, то в правой части формулы (11.8) стоит его циркуляция по контуру L.