Решение гиперболического разностного уравнения
Выражения (8.14) и (8.13) дают значения u для первых двух строк: j = 0 и j = 1.
Подставляя j = 1 в (8.11), получим
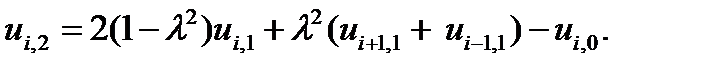
Все слагаемые в правой части этого уравнения включают значения u только из первых двух строк сетки.
Все эти значения известны из начальных условий. Поэтому в последнем уравнении имеется только одно неизвестное и все значения функции, соответствующие третьей строке, можно вычислить в явном виде.
Это же справедливо и для последующих строк. Систем уравнений решать не приходится. Таким образом, (8.11) представляет собой явную схему решения волнового уравнения.
Вопросы сходимости и устойчивости метода рассмотрим без доказательств.
Показано, что решение (8.11) (т. е. разностной схемы) сходится к решению волнового уравнения (8.7) (имеется в виду, что при h → 0 и k → 0 решение разностного уравнения асимптотически приближается к решению дифференциального уравнения), если l < 1 или, что то же самое,
| k < h. | (8.15) |
Это условие является достаточным для сходимости, но оно не является необходимым.
Другими словами, существуют уравнения и величины интервалов, при которых (8.15) не выполняется, но все же получается правильный результат.
Однако в общем случае при невыполнении (8.15) нельзя гарантировать сходимость.
Т. о., как только выбрана величина интервала разбиения h в направлении х, то появляется ограничение на величину интервала по времени.
Если необходимо произвести вычисления для большого отрезка t, может потребоваться большое количество шагов по времени.
При l > 1 метод становится неустойчивым, как в абсолютном, так и в относительном смысле. Т. е. любые ошибки возрастают в ходе вычисления решения.
Т.о., при решении уравнения (8.7) явными методами условие (8.15) обязательно должно выполняться.
Отличительная особенность всех явных методов: при их использовании должно соблюдаться некоторое условие типа (8.15), обеспечивающее сходимость и устойчивость методов.
Существуют также неявные методы решения гиперболических уравнений, не подверженные неустойчивости.
Обсудим их в следующем параграфе, посвященном решению параболических уравнений. Все основные идеи этого параграфа можно без труда обобщить на случай гиперболических уравнений.
8.3 ДУ в частных производных. Параболические уравнения
Уравнения параболического типа получаются, если в уравнении (8.1) выполняется условие B2 – 4AC = 0.
Типичная физическая задача – процесс теплопередачи по длинному стержню, лежащему вдоль оси х от х = 0 до х = L.
Предположим, что в точке х = 0 температура поддерживается на уровне Т0, а в точке х = L температура поддерживается на уровне TL.
Предположим также, что в момент времени t = 0 распределение температуры вдоль стержня задавалось функцией f(x).
Тогда распределение температуры вдоль стержня во все последующие моменты времени дается решением уравнения
| uxx = aut. | (8.16) |
В уравнении (8.16) u – температура стержня в данной точке в данныймомент времени, постоянная а зависит от физических свойств стержня. Для простоты положим а = 1, так что уравнение сведется к виду:
| uxx = ut. | (8.17) |
Граничные условия:
| u(0, t) = T0, u(L, t) = TL. | (8.18) |
Начальное условие:
| u(x, 0) = f(x). | (8.19) |
Уравнение (8.17) представляет собой параболическое дифференциальное уравнение в частных производных.
Его называют уравнением теплопередачи, или уравнением диффузии.
При записи в разностной форме граничные условия (8.18) запишутся в виде:
| u0, j = T0 ; j = 1, 2, …, un, j = TL ; j = 1, 2, … | (8.20) |
Начальное условие имеет вид:
| ui,0 = f(ih). | (8.21) |
Чтобы преобразовать в разностную форму уравнение (8.17), введем сетку, охватывающую область 0 £ х £ L и t > 0 с интервалом разбиения h в направлении x и интервалом разбиения k в направлении t.
С использованием (7.1) и (7.3) получаем
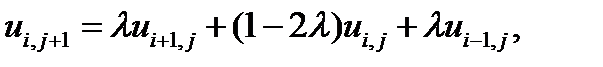 | (8.22) |
где
| l = k/h2. | (8.23) |
В выражении (8.22) индекс i изменяется от 1 до n – 1, а индекс j – от 1 до ¥.
Верхний предел ошибки ограничения:
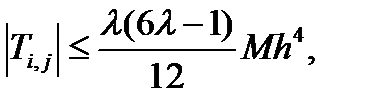
где
|uxxxx| < M
при условии l ¹ 1/6.
При l = 1/6
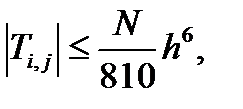
где
|uxxxxxx| < N.
