Предельные теоремы в схеме Бернулли

Если число испытаний п велико, то вычисления по формуле Бернулли становятся затруднительными. В то же время большие значения п позволяют заменять эту формулу приближенными асимптотическими формулами. Рассмотрим три такие формулы.

Теорема2.5. (формула Пуассона)Если 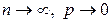так, что 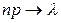, то

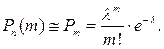(2.5)

Формула (2.5) дает хорошие результаты, если npq<9. Если же npq>9, то для вычисления вероятности 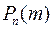можно воспользоваться локальной теоремой Лапласа.

Теорема 2.6.(локальная теорема Муавра–Лапласа). Вероятность появления события т раз в п независимых испытаниях при больших значениях п приближенно определяется по формуле

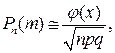(2.6)

где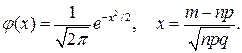

Теорема 2.7.(интегральная теорема Муавра–Лапласа). Вероятность того, что число появлений события в п независимых испытаниях находится в пределах т₁£ т £ т₂ и при больших значениях п приближенно определяется по формуле

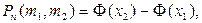(2.7)

где

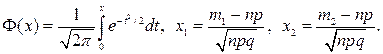
Функция Ф(х) называется функцией Лапласа. Для функций 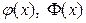имеются таблицы ее значений. Функция 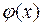является четной, а функция Ф(х) – нечетной, т.е. 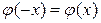; Ф(– х)= – Ф(х);

Из интегральной теоремы Лапласа можно вывести формулу для вероятности отклонения относительной частоты т/п события в серии испытаний от постоянной вероятности р этого события в одном испытании:

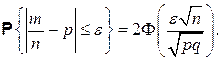(2.8)

Пример 2.21. Завод отправил на базу 500 изделий. Вероятность повреждения изделия в пути равна 0.002. Найти вероятность того, что в пути будут повреждены три изделия.

Решение. Можно считать, что имеем дело со схемой Бернулли, в которой испытания проводятся 500 раз. Так как число п=500 достаточно велико, а вероятность p=0.002 мала (причем npq=500×0.002×0.998»2<9), то воспользуемся приближенной формулой (2.5), где l=np =500×0.002=1:

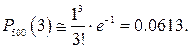
Пример 2.22. Найти вероятность того, что событие происходит 80 раз в 400–х испытаниях, если вероятность этого события в каждом испытании равна 0.2.

Решение. Здесь п=400 достаточно велико, но величина npq также велика (npq=400×0.2×0.8=64>9), поэтому воспользуемся формулой (2.6). Вычисляем

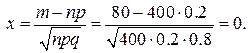
По таблице функции 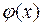находим 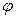(0)=0.3989. Окончательно получаем:

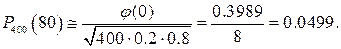
Пример 2.23. Найти вероятность того, что в 400–х испытаниях событие произойдет не более 70–ти раз, если вероятность появления этого события в каждом испытании равна 0.2.

Решение. Воспользуемся интегральной теоремой Лапласа для вычисления вероятности :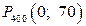

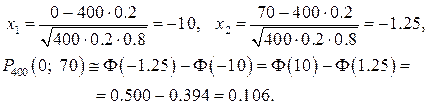
Пример 2.24. Определим, сколько надо провести испытаний, чтобы с вероятностью 0.95 относительная частота выпадения «орла» отличалась от вероятности р=0.5этого события не более чем на 5%.

Решение. Воспользуемся формулой (2.8). В нашем случае р=0.5, q=0.5, e=0.5 0.05=0.025. По условию задачи

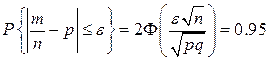
или Пользуясь таблицей функции Лапласа, по значению функции находим значение аргумента:

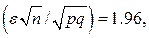т.е.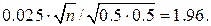

Отсюда находим, что п=1536.64. Таким образом, надо провести не менее чем 1537 испытаний.

СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

Понятие случайной величины

Случайной величиной называется величина, которая в результате испытаний, проводимых в одних и тех же условиях, принимает различные, вообще говоря, значения, зависящие от не учитываемых случайных факторов. Примеры случайных величин: число выпавших очков на игральной кости, число дефектных изделий в партии, отклонение точки падения снаряда от цели, время безотказной работы устройства и т.п. Различают дискретные и непрерывные случайные величины. Дискретной называется случайная величина, возможные значения которой образуют счетное множество, конечное или бесконечное (т.е. такое множество, элементы которого могут быть занумерованы).

Непрерывной называется случайная величина, возможные значения которой непрерывным образом заполняют некоторый конечный или бесконечный интервал числовой оси. Число значений непрерывной случайной величины всегда бесконечно.

Случайные величины будем обозначать заглавными буквами конца латинского алфавита: X, Y, ...; значения случайной величины – строчными буквами: х, у, ... . Таким образом, X обозначает всю совокупность возможных значений случайной величины, а х – некоторое ее конкретное значение.