Теоремы Чебышева и Бернулли.

Теорема 6.2 (теорема Чебышева). Если Х₁, Х₂,…, Х_п – попарно независимые случайные величины, дисперсии которых равномерно ограничены ( D(X_i) ≤ C), то для сколь угодно малого числа ε вероятность неравенства

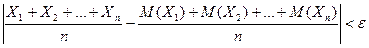
будет сколь угодно близка к 1, если число случайных величин достаточно велико.

Замечание. Иначе говоря, при выполнении этих условий

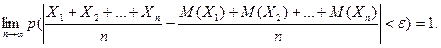
Доказательство. Рассмотрим новую случайную величину 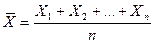и найдем ее математическое ожидание. Используя свойства математического ожидания, получим, что 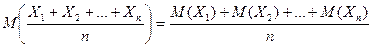. Применим к 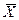неравенство Чебышева: 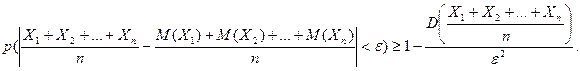Так как рассматриваемые случайные величины независимы, то, учитывая условие теоремы, имеем: 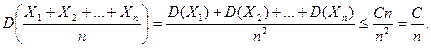Используя этот результат, представим предыдущее неравенство в виде:

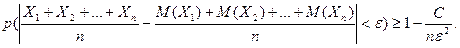Перейдем к пределу при 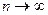: 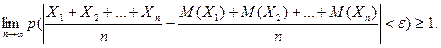Поскольку вероятность не может быть больше 1, можно утверждать, что

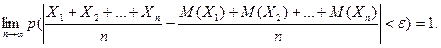Теорема доказана.

Следствие.

Если Х₁, Х₂, …, Х_п – попарно независимые случайные величины с равномерно ограничен-ными дисперсиями, имеющие одинаковое математическое ожидание, равное а, то для любого сколь угодно малого ε > 0 вероятность неравенства 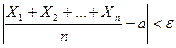будет как угодно близка к 1, если число случайных величин достаточно велико. Иначе говоря, .

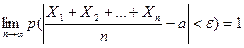Вывод: среднее арифметическое достаточно большого числа случайных величин прини-мает значения, близкие к сумме их математических ожиданий, то есть утрачивает характер случайной величины. Например, если проводится серия измерений какой-либо физической величины, причем: а) результат каждого измерения не зависит от результатов остальных, то есть все результаты представляют собой попарно независимые случайные величины; б) измерения производятся без систематических ошибок (их математические ожидания равны между собой и равны истинному значению а измеряемой величины); в) обеспечена определенная точность измерений, следовательно, дисперсии рассматривае-мых случайных величин равномерно ограничены; то при достаточно большом числе измерений их среднее арифметическое окажется сколь угодно близким к истинному значению измеряемой величины.

Теорема Бернулли.

Теорема 6.3 (теорема Бернулли). Если в каждом из п независимых опытов вероятность р появления события А постоянна, то при достаточно большом числе испытаний вероят-ность того, что модуль отклонения относительной частоты появлений А в п опытах от р будет сколь угодно малым, как угодно близка к 1:

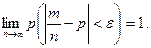(6.6.)

Доказательство. Введем случайные величины Х₁, Х₂, …, Х_п, где X_i – число появлений А в i-м опыте. При этом X_i могут принимать только два значения: 1(с вероятностью р) и 0 (с вероятностью q = 1 – p). Кроме того, рассматриваемые случайные величины попарно независимы и их дисперсии равномерно ограничены (так как D(X_i) = pq, p + q = 1, откуда pq ≤ ¼ ). Следовательно, к ним можно применить теорему Чебышева при M_i = p:

.

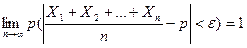Но 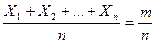, так как X_i принимает значение, равное 1, при появлении А в данном опыте, и значение, равное 0, если А не произошло. Таким образом,

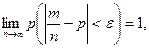
что и требовалось доказать.

Замечание. Из теоремы Бернулли не следует, что 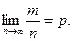Речь идет лишь о вероятно-сти того, что разность относительной частоты и вероятности по модулю может стать сколь угодно малой. Разница заключается в следующем: при обычной сходимости, рассматриваемой в математическом анализе, для всех п, начиная с некоторого значения, неравенство 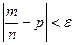выполняется всегда; в нашем случае могут найтись такие значения п, при которых это неравенство неверно. Этот вид сходимости называют сходимостью по вероятности.

Лекция 7.

Системы случайных величин. Закон распределения вероятностей дискретной двумерной случайной величины. Функция распределения и плотность распределения двумерной случайной величины, их свойства. Вероятность попадания случайной точки в произвольную область. Отыскание плотностей вероятности составляющих двумерной случайной величины

Наряду с одномерными случайными величинами, возможные значения которых определяют-ся одним числом, теория вероятностей рассматривает и многомерные случайные величины. Каждое возможное значение такой величины представляет собой упорядоченный набор нескольких чисел. Геометрической иллюстрацией этого понятия служат точки п-мерного пространства, каждая координата которых является случайной величиной (дискретной или непрерывной), или п-мерные векторы. Поэтому многомерные случайные величины называют еще случайными векторами.