Tема 3 Приложения производной

Задача 4. Исследовать функцию 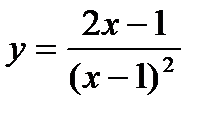и построить ее график.

Решение: Исследование функции проведем по следующей схеме:

1. Найдем область определения функции.

2. Исследуем функции на непрерывность.

3. Установим, является ли данная функция четной, нечетной.

4.Найдем интервалы возрастания и убывания функции и точки экстремума.

5. Найдем интервалы выпуклости и вогнутости кривой и точки ее перегиба.

6. Найдем асимптоты кривой.

Реализуем указанную схему:

1. Функция определена при всех значениях аргумента х, кроме х=1.

2. Данная функция является элементарной, поэтому она непрерывна на своей области определения, т. Е. на интервалах ( 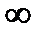; 1) и (1; 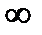). В точке х=1 функция терпит разрыв второго рода.

3. Для установления четности или нечетности функции проверим выполнимость равенств f(-х) =f(x) (тогда f(x)— четная функция) или f(-х) =-f(х) (для нечетной функции) для любых х и – х из области определения функции:

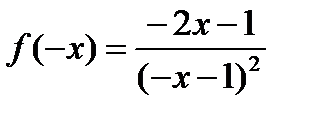
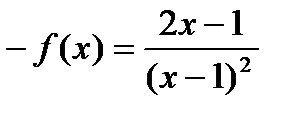
Следовательно, f( - х) 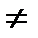f(x) и f( - x) 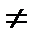- f(x), то есть данная функция, не является ни четной, ни нечетной.

4. Для исследования функции на экстремум найдем её первую производную:

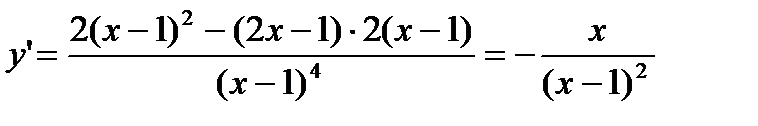
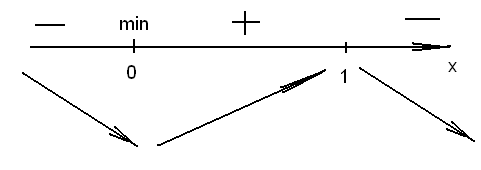
у'=0 при х=0 и у' не существует при х=1. Тем самым имеем две критические точки: х₁=0, х₂=1. Но точка х₂=1 не принадлежит области определения функции, экстремума в ней быть не может Разобьем числовую ось на три интервала (рис. 2),-( ; 0), (0; 1),(1; ). В первом и третьем интервалах первая производная отрицательна, следовательно, здесь функция убывает; во втором интервале — положительна и данная функция возрастает. При переходе через точку х=0 первая производная меняет свой знак с минуса на плюс, поэтому в этой точке функция имеет минимум: y_min=y(0)=-1. Значит, А(0; — 1) — точка минимума.

Рис.2

На рис. 2 знаками +, - указаны интервалы знакопостоянства производной y', а стрелками - возрастание и убывание исследуемой функции.

5. Для определения точек перегиба графика функции, интервалов выпуклости и вогнутости кривой найдем вторую производную:

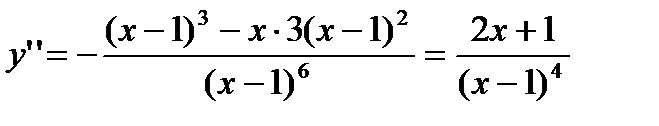
y''=0 при х= 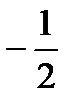и у'' не существует при х= l. Разобьем числовую ось на три интервала (рис. 6); ( 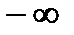; 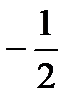), ( 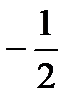; 1), (1; 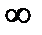). На первом интервале вторая производная у'' отрицательна и дуга исследуемой кривой выпукла; на вто-ром итретьем интервалах у''>0, тем самым график является вогнутым. При переходе через точку х= 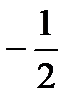у'' меняет свой знак, поэтому х= 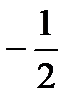— абсцисса точки перегиба.

Следовательно, В 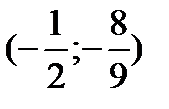— точка перегиба графика функции.

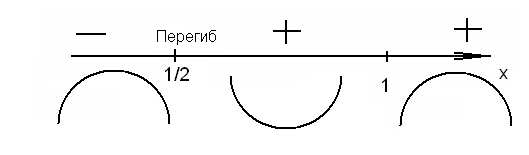
Рис. 3

6. х=1 – точка разрыва функции, 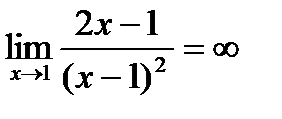.Поэтому прямая х=1 является вертикальной асимптотой графика. Для определения уравнения наклонной асимптоты y=kx+b воспользуемся формулами: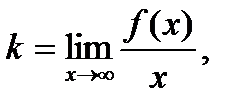

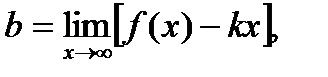
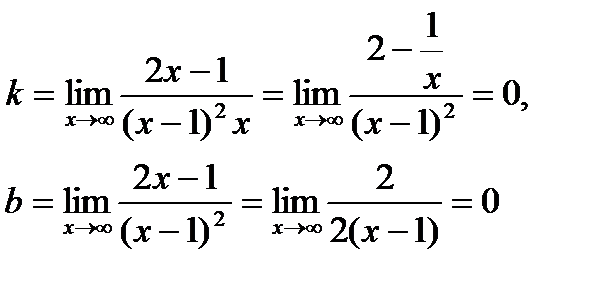
При вычислении последнего предела использовалось правило Лопиталя.

Значит прямая у=0 есть горизонтальная асимптота графика исследуемой функции, представленного на рис. 4.

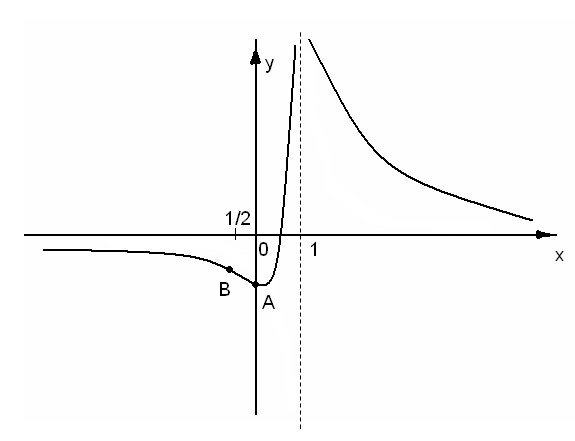
Рис.4

Задача 5. Резервуар, имеющий форму открытого сверху прямоугольного параллелепипеда с квадратным дном, нужно вылудить внутри оловом. Каковы должны быть размеры резервуара при его емкости 108 л воды, чтобы затраты на его лужение были наименьшими?

Решение. Затраты на покрытие резервуара оловом будут наименьшими, если при данной вместимости его поверхность будет минимальной.

Обозначим через а сторону основания, b — высоту резервуара. Тогда площадь S его поверхности равна а²+4ab, а объем V=а²b=108. Отсюда

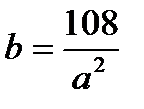и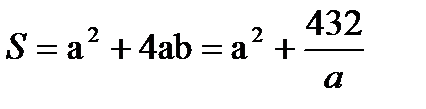

Полученное соотношение устанавливает зависимость между площадью, поверхности резервуара S (функция) и стороной основания а (аргумент). Исследуем функцию S на экстремум. Найдем первую производную S', приравняем ее к нулю и решим полученное уравнение:

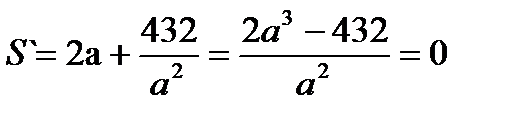
Отсюда, а=6. S`(а)>0 при а>6, S'(а) <0 при а<6. Следовательно, при а=6 функция S имеет минимум. Если, а=6, то b=3. Таким образом, затраты на лужение резервуара емкостью 108 л будут наименьшими, если он имеет размеры 6дм 6 дм 3 дм.

Вопросы для самопроверки

1. Сформулируйте теоремы Ролля, Лагранжа. Каков их геометрический смысл?

2. Какая функция называется возрастающей? Убывающей?

3. Сформулируйте необходимый, достаточный признаки возрастания и убывания функции.

4. Какие точки называются стационарными? Критическими?

5. Назовите достаточные признаки экстремума функции.

6. Какая кривая называется выпуклой? Вогнутой?

7. Как найти интервалы выпуклости и вогнутости кривой?

8. Сформулируйте достаточный признак существования точки перегиба кривой.

9.Что называется асимптотой кривой? Как найти вертикальные и наклонные асимптоты?

10. Назовите схему исследования функции и построения ее графика?

11.В каком случае применяется правило Лопиталя при вычислении пределов?