Чтобы решить однородное уравнение, нужно

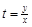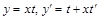1. ввести подстановку или и упростить полученное уравнение;

2. разделить переменные и проинтегрировать уравнение;

3. результат интегрирования упростить, пропотенцировать, если нужно, и записать общий интеграл, вернувшись к исходной переменной.

Линейныеуравнения. Уравнение называется линейным, если функция, а также ее производная входят в него в первой степени (линейно), т.е. уравнение вида

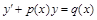. (6.4)

Если 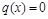, то уравнение называется однородным; если 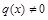- неоднородным. Общее решение однородного линейного уравнения получается путем разделения переменных; общее решение неоднородного уравнения получается из общего решения соответствующего однородного уравнения с помощью вариации произвольной постоянной интегрирования C.

Данное линейное уравнение можно интегрировать также с помощью замены 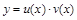, где 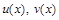- две неизвестные функции. Для определения u и v можно составить две идентичные системы. Подставьте 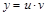и 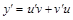в уравнение (6.4) и убедитесь в этом сами

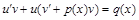(6.5)

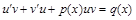
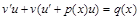(6.6)

Из уравнений (6.5) получается одна система, 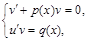а из (6.6) − вторая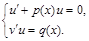

В каждой из систем первое уравнение выбрано произвольно потому, что две неизвестные u и v нельзя найти из одного уравнения. Пользоваться можно любой системой.

Что необходимо для решения линейных уравнений

Прежде всего, нужно проверить признаки линейного уравнения: 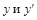входят в уравнение в первой степени (линейно). Затем следует выполнить следующие операции:

1) Положить 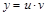, тогда 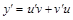и подставить 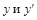в уравнение (6.4).

2) Составить систему для определения u и v. Решить ее (допустим относительно v) . При определении v не нужно писать произвольную постоянную, ибо 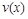достаточно знать с точностью до постоянной величины.

3) Подставить в уравнение 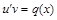величину v и решить полученное уравнение.

4) Записать ответ 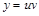, используя пункты 2) и 3).

5) Чтобы найти частное решение, нужно начальное условие подставить в общее решение и определить C.

Уравнение Бернулли. Одним из уравнений, сводящимся к линейным уравнениям, является уравнение Бернулли, которое имеет вид

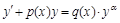, (6.7)

где α − любое вещественное число, кроме 0 и 1.

Чтобы свести уравнение (6.7) к линейному уравнению, нужно поделить обе его части на выражение 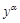: 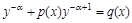. Положить 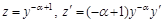, тогда 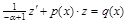− линейное уравнение, которое можно решать методом замены переменной или методом вариации, а затем найти y из замены .

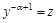3. Дифференциальные уравнения высших порядков, допускающие понижение порядка.

1. Уравнение n-го порядка 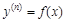(не содержит явно 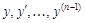) решается последовательным интегрированием.

2. Уравнение 2-го порядка 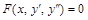(не содержит явно искомой функцииy) преобразуется в уравнение 1-го порядка посредством подстановки 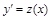(откуда ).

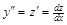3. Уравнение 2-го порядка 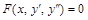(не содержит явно аргументаx) преобразуется в уравнение 1-го порядка посредством подстановки 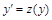(откуда ).

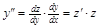Что необходимо для решения