Абсолютные и средние показатели вариации и способы их расчета.

Для характеристики колеблемости признака рассчитываются:

Размах вариации: R = X_max – X_min.

Обобщающую характеристику распределению отклонений дает среднее линейное отклонение, которое учитывает различия всех единиц изучаемой совокупности, рассчитывается по формуле: .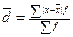

На практике меру вариации более объективно отражает показатель дисперсии (средний квадрат отклонений), рассчитываемый для генеральной совокупности в целом по формуле: .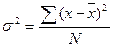

Для интервального ряда распределения: .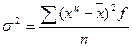

Среднее квадратическое отклонение s - корень квадратный из дисперсии. Чем оно меньше, тем лучше средняя арифметическая отражает собой всю представляемую совокупность.

Показатели относительного рассеивания:

1. Коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг средней: .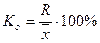

2. Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений от средней величины: .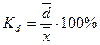

3. Коэффициент вариации – наиболее распространенный показатель колеблемости, ипользуемый для оценки типичности средних величин : 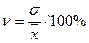. Если вариация больше 40%, то это говорит о большой колеблемости признака в изучаемой совокупности.

Виды дисперсий и закон (правило) сложения дисперсий.

1. Общая дисперсия характеризует вариацию признака, которая зависит от всех условий в данной совокупности. Исчисляется общая дисперсия по формуле:

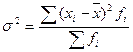, где - общая средняя для всей изучаемой совокупности.

2. Межгрупповая дисперсия – отражает вариацию изучаемого признака, которая возникает под влиянием признака-фактора, положенного в основу группировки. Она характеризует колеблемость групповых (частных) средних 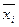около общей средней 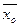. Межгрупповая дисперсия вычисляется по формуле:

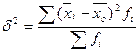, где 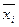- средняя по отдельным группам, f_i – численность отдельных групп.

Средняя по каждой группе может быть рассчитана по формуле: .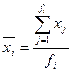

3. Средняя внутригрупповых дисперсий характеризует случайную вариацию в каждой отдельной группе. Эта вариация возникает под влиянием других, не учитываемых факторов, и не зависит от условия (признака-фактора), положенного в основу группировки. Определяется она по формуле:

,

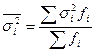причем, дисперсия по каждой группе рассчитывается относительно средней внутригрупповой: .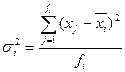

Общая дисперсия равна сумме величин межгрупповой дисперсии и средней из внутригрупповых дисперсий:

.

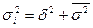Это правило (закон) сложения вариаций (дисперсий) имеет большую практическую значимость, так как позволяет выяснить зависимость результатов от определяющих факторов соотношением межгрупповой и общей дисперсии (коэффициент детерминации):

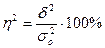. Показывает процент различий вариантов от их группировки.

Дисперсия альтернативного (качественного) признака.

Альтернативными являются признаки, которыми обладают одни единицы изучаемого признака и не обладают другие. Наличие изучаемого признака обозначается 1, а его отсутствие – 0. Доля вариантов, обладающих изучаемым признаком, обозначается p, а доля вариантов, не обладающих признаком, обозначается q. Следовательно, p + q = 1.

Найдем их среднее значение и дисперсию:

.

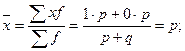
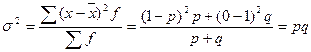p + q не может быть больше 1, а pq не может быть больше 0,25.

Для анализа однородности начисления рассчитайте децильный и квартильный коэффициенты расслоения.

Децильный коэффициент рассчитывается как отношение суммарного значения показателя для десяти процентов элементов с наибольшим значением признака к сумме десяти процентов с наименьшими показателями.

Для расчета квартильного коэффициента сравниваются верхняя и нижняя четверти распределения.

В вашей работе по интервальному ряду распределения по итоговому начислению рассчитайте все показатели вариации. Сделайте выводы.

Лабораторная работа №5.