Модульная единица 1.9. Статистическое изучение связей
1.9.1 Понятие о взаимосвязях. Методы выявления и измерения взаимосвязей
В природе, и тем более в обществе, все явления взаимосвязаны между собой. Урожайность зависит от качества почвы, внесения удобрений, обеспеченности производственными фондами и от многих других факторов; производительность труда от производственных затрат, обеспеченности основными и оборотными фондами и т.д.; среднедневная температура от времени года, местоположения страны удаленности от океана и т.д. Соответственно, что бы прогнозировать, то есть управлять развитием явлений, общественных и природных, необходимо установить связи, существующие между интересующими нас явлениями, их силу, вид, направление и т.д.
Так как, в статистике изучают детерминированность следствия факторами (детерминизм – обусловленность явлений множеством факторов) будем называть признак (явление) характеризующий следствие результативным признаком (зависимым признаком, результатом). Признаки, характеризующие факторы – факторными признаками (независимыми признаками). Результативные признаки принимают то или иное значение под влиянием на них признаков факторных. Соответственно размер результативного признака есть результат влияние на него факторных признаков.
В статистике различают два вида взаимосвязей между явлениями: функциональная и корреляционная.
Функциональная связь – это связь, жестко детерминированная или полная (связь равная единице или 100%), размер результативного признака зависит только от одного фактора, причем каждому конкретному значению факторного признака может соответствовать одно, или несколько четко заданных значений результативного признака.
Строго определить функциональную связь можно, только придав ей математическую формулировку. Функциональной связью является, например, связь вида:
а) 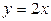 , при
, при 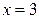 ,
, 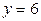
б) 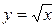 , при
, при 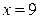 ,
, 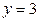 , или
, или 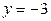
Видно, что величина признака 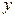 зависит, лишь от признака
зависит, лишь от признака 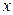 , причем строго определенным образом.
, причем строго определенным образом.
Но, в мире природы и тем более в обществе функциональных связей не бывает – все явления реального мира взаимосвязаны между собой. И поэтому функциональная связь – это связь абстрактная, упрощающая расчеты, но и упрощающая объективно существующую реальность. Тем не менее, представление о связях как связях функциональных используют такие науки как химия, физика, механика, электротехника и т.д.
Обратная величина функциональной связи – это отсутствие связи (связь между явлениями равна нулю), размер результативного признака совершенно не зависит от какого-то фактора. Отсутствие связи, как и связь функциональная не существует в реальном мире – это также абстрактное понятие, упрощающее расчеты и соответственно реальность.
Корреляционная связь – это связь схоластически детерминированная, неполная. При корреляционной связи каждому значению факторного признака (признаков) соответствует множество значений результативного признака. Корреляционная связь проявляется лишь при большом числе наблюдений, в среднем.
Также различают формы связи:
1.прямая связь – с возрастанием величины фактора наблюдается рост величины результата, а при уменьшении величины фактора уменьшение величины результативного признака.
2. обратная связь – с увеличением величины фактора величина результативного признака уменьшается, а с уменьшением увеличивается.
Кроме того, по математическому выражению, связи делятся на линейные и нелинейные.
При изучении взаимосвязей общественных явлений используют различные методы, такие как:
1. сопоставление параллельных рядов;
2. метод аналитических группировок;
3. корреляционно-регрессионный анализ;
4. и др.
Изучение взаимосвязей позволяет решить следующие задачи:
1. определить наличие связи;
2. определение формы связи;
3. измерение тесноты связи;
4. прогнозирование изменения результативного признака под влиянием изменения фактора (факторов).
1.9.2 Метод сопоставления параллельных рядов. Корреляция альтернативных признаков
1.9.2.1 Метод сопоставления параллельных рядов
Метод сопоставления параллельных рядов является наиболее простым методом исследования взаимосвязей между явлениями.
Данный метод заключается в сопоставлении ранжированного ряда факторного признака с ранжированным рядом результативного признака. Данное сопоставление позволяет определить наличие или отсутствие связи между явлениями, а также ее направление.
Также метод параллельных радов позволяет определить тесноту связи. Для этого рассчитывают коэффициент Фехнера и коэффициент корреляции рангов Спирмена.
Расчет коэффициента Фехнера.
Для расчета данного коэффициента необходимо рассчитать отклонения значений признаков 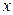 и
и 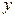 от их средних значений
от их средних значений 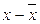 и
и 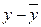 , при этом определяют знак отклонений
, при этом определяют знак отклонений 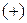 или
или 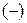 . Если знаки отклонений у признаков
. Если знаки отклонений у признаков 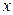 и
и 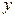 совпадают, то делается вывод о согласованности вариации, если не совпадают – вариация несогласованна. Формула расчета коэффициента Фехнера:
совпадают, то делается вывод о согласованности вариации, если не совпадают – вариация несогласованна. Формула расчета коэффициента Фехнера:
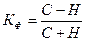 (9.1)
(9.1)
где:
С – число совпавших знаков отклонений 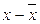 и
и 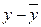
Н – число не совпавших отклонений 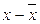 и
и 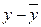
Коэффициент Фехнера может принимать значения от 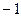 до
до 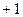 . В статистике принято считать, что до 0,3 связь слабая, от 0,3 до 0,7 связь средняя, свыше 0,7 связь сильная. Знак плюс показывает, что связь прямая, знак минус – связь обратная.
. В статистике принято считать, что до 0,3 связь слабая, от 0,3 до 0,7 связь средняя, свыше 0,7 связь сильная. Знак плюс показывает, что связь прямая, знак минус – связь обратная.
Необходимо учитывать, что коэффициент Фехнера определяет направление связи, но дает лишь очень грубую оценку ее величины.
Коэффициент корреляции рангов Спирмена
Коэффициент корреляции рангов учитывает согласованность рангов единиц совокупности.
Ранг – номер, который занимает единица совокупности по признакам 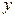 и
и 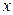 .
.
Формула расчета коэффициента корреляции рангов:
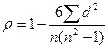 (9.2)
(9.2)
где: 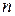 – число единиц совокупности,
– число единиц совокупности,
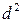 – квадрат разности рангов.
– квадрат разности рангов.
Коэффициент корреляции рангов может принимать значения в интервале 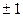 .
.
1.9.2.2 Корреляция альтернативных признаков
В случае, когда имеются противоположные по значению варианты признака, говорят об альтернативном признаке (да, нет). Например, продукция может быть годной или не годной, животное может быть кошкой или не кошкой.
Для исследования взаимосвязей между двумя альтернативными признаками, то есть, вариация обоих атрибутивных признаков ограничена двумя группами, используют «тетрахорические показатели». Их расчет основан на использовании определенной расчетной таблицы (табл. 9.1).
Таблица 9.1
| II I | + | - |
| + | a | b |
| - | c | d |
Она состоит из четырех ячеек обозначенных буквами a, b, c, d – частоты, расположенные в I, II, III, IV квадрантах. Знаки 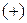 и
и 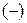 в заголовках столбцов и строк характеризуют наличие или отсутствие альтернативного признака.
в заголовках столбцов и строк характеризуют наличие или отсутствие альтернативного признака.
К «тетрахорическим показателям» относят:
· коэффициент ассоциации Пирсона
· коэффициент коллигации Юла
· коэффициент контингенции Юла и Кендэла
· коэффициент Шарлье и др.
Рассмотрим некоторые из них.
Коэффициент ассоциации Пирсона, данный коэффициент используют для измерения тесноты взаимосвязи надежности и годности. Рассчитывается по формуле:
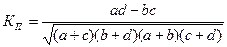 (9.3)
(9.3)
Коэффициент коллигации Юла рассчитывается как:
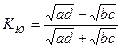 (9.4)
(9.4)
Данный коэффициент показывает средний размер связи.
Рассмотренные коэффициенты могут принимать значения от 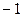 до
до 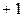 .
.
Если при измерении связи между качественными показателями образуется более двух групп, для определения тесноты связи используют:
· коэффициент взаимной сопряженности Пирсона
· коэффициент взаимной сопряженности Чупрова
· коэффициент взаимной сопряженности Крамера и. д.р.
Коэффициент взаимной сопряженности Пирсона рассчитывается:
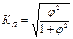 (9.5)
(9.5)
Коэффициент взаимной сопряженности Чупрова рассчитывается:
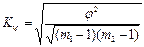 (9.6)
(9.6)
где:
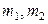 – число групп по первому и второму признаку соответственно.
– число групп по первому и второму признаку соответственно.
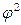 – показатель взаимной сопряженности
– показатель взаимной сопряженности
Коэффициент взаимной сопряженности Чупрова целесообразно использовать, когда число групп по каждому признаку одинаково 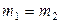 . Если
. Если 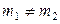 используют коэффициент Крамера.
используют коэффициент Крамера.
Показатель взаимной сопряженности 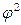 рассчитывают, используя вспомогательную таблицу (табл. 9.2)
рассчитывают, используя вспомогательную таблицу (табл. 9.2)
Данные подставляют в формулу:
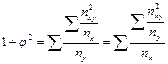 (9.7)
(9.7)
Таблица 9.2 - Вспомогательная таблица для расчета показателя взаимной сопряженности
| y x | I | II | III | Итого |
| I | … | … | 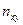 | 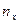 |
| II | … | … | 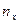 | |
| III | … | … | 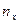 | |
| Итого |  |  |  | 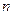 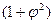 |
Коэффициент взаимной сопряженности Крамера рассчитывается:
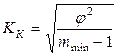 (9.8)
(9.8)
где:
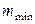 – минимальное, из значений
– минимальное, из значений  и
и 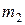
При 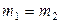 значения коэффициентов Чупрова и Крамера совпадают.
значения коэффициентов Чупрова и Крамера совпадают.
1.9.3 Метод аналитических группировок
Этот метод позволяет определить взаимосвязи между двумя и более признаками.
В ходе построения аналитической группировки необходимо решить следующие вопросы:
1. выбор факторных признаков
2. определение числа групп
3. оценка линии регрессии
4. измерения тесноты связи
Выбор факторных признаков
Выбор основывается на всестороннем анализе изучаемого явления, экономической теории, опыте и знаниях исследователя и т.д.
Определение числа групп
В принципе, чем больше число групп, тем точнее будет описана линия регрессии, но в месте с тем снижается точность расчета средних.
В данном вопросе необходимо, что бы увеличение числа групп, для более точного описания линия регрессии, не привело к утрате закономерного характера линии регрессии, из-за малочисленности групп.
Границы интервалов групп определяют, выделяя основные типы изучаемых явлений. При расчете величин интервалов возможно использование следующей формулы предложенной американским ученым Стерджессом.
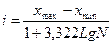 (9.9)
(9.9)
где:
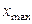 – максимальное значение признака в совокупности
– максимальное значение признака в совокупности
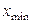 – минимальное значение признака в совокупности
– минимальное значение признака в совокупности
N – число единиц в совокупности.
При разбиении изучаемой совокупности рекомендуется соблюдение принципа равных частот, т.е. образование групп с примерно одинаковой численностью единиц.
Оценка линии регрессии
Оценка линии регрессии в данном случае основывается на вычислении среднего значения признака 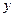 для интервала значений признака
для интервала значений признака 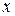 .
.
В качестве группировочного признака, как правило, используется факторный признак.
Показатель, характеризующий влияние факторного признака на результативный признак называется показателем силы связи 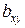 , который показывает, на сколько единиц изменится результативный признак, если факторный увеличится на одну единицу.
, который показывает, на сколько единиц изменится результативный признак, если факторный увеличится на одну единицу.
Если связь между признаками нелинейная, то есть, существенно изменяется при переходе от одной группе к другой, рассчитывается как:
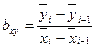 (9.10)
(9.10)
Так, например, если совокупность разбита на четыре группы, рассчитывают
1) 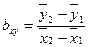 ; 2)
; 2) 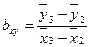 ; 3)
; 3) 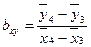
где:
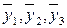 – средне-групповые значения результативного признака.
– средне-групповые значения результативного признака.
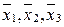 – средние значения (или середины интервалов) факторного признака.
– средние значения (или середины интервалов) факторного признака.
Для группировочного признака, среднюю величину находят как середину интервала.
В случае линейной связи важным показателем является поазатель среднейсилы связи 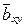 .
.
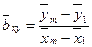 (9.11)
(9.11)
где:
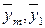 – средние значения результативного признака в последней и первой группах соответственно;
– средние значения результативного признака в последней и первой группах соответственно;
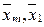 – середины интервалов (или средние значения) факторного признака в последней и первой группах.
– середины интервалов (или средние значения) факторного признака в последней и первой группах.
Измерение тесноты связи
Измерение тесноты связи в аналитических группировках основано на правиле сложения дисперсий – общая дисперсия всегда равна сумме средней внутригрупповой и межгрупповой дисперсий:
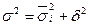 (9.12)
(9.12)
где:
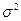 – общая дисперсия, характеризует вариацию признака во всей совокупности, сложившуюся под влиянием всех факторов и условий:
– общая дисперсия, характеризует вариацию признака во всей совокупности, сложившуюся под влиянием всех факторов и условий:
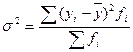 или
или 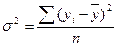 (9.13)
(9.13)
где 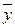 – общая средняя.
– общая средняя.
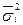 – средняя внутригрупповая дисперсия, оценивает вариацию признака, сложившуюся по влиянием других, неучтенных в данном исследовании факторов и независящую от фактора группировки. Она определяется как средняя из групповых дисперсий:
– средняя внутригрупповая дисперсия, оценивает вариацию признака, сложившуюся по влиянием других, неучтенных в данном исследовании факторов и независящую от фактора группировки. Она определяется как средняя из групповых дисперсий:
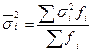 или
или 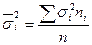 (9.14)
(9.14)
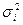 – внутригрупповая (случайная) дисперсия,
– внутригрупповая (случайная) дисперсия,
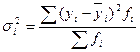 или
или 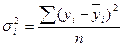 (9.15)
(9.15)
где 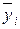 – групповая средняя.
– групповая средняя.
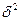 – межгрупповая (систематическая) дисперсия, измеряет систематическую вариацию, обусловленную влиянием фактора, по которому произведена группировка:
– межгрупповая (систематическая) дисперсия, измеряет систематическую вариацию, обусловленную влиянием фактора, по которому произведена группировка:
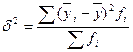 (9.16)
(9.16)
Показателем тесноты связи между признаками в аналитической группировке служит корреляционное отношение:
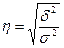 (9.17)
(9.17)
Корреляционное отношение может принимать значения от 0 до 1. Принято считать, что до 0,3 связь слабая, от 0,3 до 0,7 связь средняя, свыше 0,7 связь сильная. Чем больше корреляционное отношение, тем больше фактор, положенный в основание группировки, оказывает влияние на общую вариацию результативного признака, то есть они более тесно взаимосвязаны.
Квадрат корреляционного отношения – коэффициент детерминации:
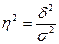 (9.18)
(9.18)
Показывает долю вариации результативного признака обусловленную включенным в модель фактором.
1.9.4 Корреляционно-регрессионный анализ
Корреляция – взаимосвязь между признаками, заключается в изменении средней величины результативного признака в зависимости от значения фактора (факторов).
Регрессия – функция, позволяющая по величине одного корреляционно связанного признака вычислять средние значения другого.
Корреляция, регрессия парная – корреляция, регрессия между двумя признаками: результативным 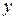 и факторным
и факторным 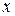 .
.
Корреляция, регрессия множественная – взаимосвязь между несколькими признаками (тремя и более), один из которых является результативным признаком 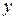 , другие факторными признаками
, другие факторными признаками 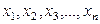 .
.
Корреляция линейная – корреляционная зависимость между признаками носящая линейный характер.
Корреляция нелинейная – корреляционная зависимость между признаками не носит линейный характер, а выражена соответствующей кривой – парабола, гипербола, экспонента, показательная функция и т.д.
Регрессия линейная – регрессионная функция, выраженная уравнение прямой.
Регрессия нелинейная – регрессионная функция выражена соответствующей нелинейной функцией – парабола, гипербола, экспонента, показательная функция и т.д.
Парная корреляционно-регрессионная модель строится для изучения взаимосвязи между результативным признаком 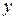 и одним фактором
и одним фактором 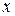 . Применяется в случае доминирующего влияния на результат лишь одного фактора, остальные факторы оказывают на результат несущественное влияние. Модель парной регрессии имеет вид:
. Применяется в случае доминирующего влияния на результат лишь одного фактора, остальные факторы оказывают на результат несущественное влияние. Модель парной регрессии имеет вид: 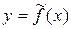 .
.
Множественная корреляционно-регрессионная модель применяется, когда необходимо изучить влияние на результативный признак не одного, а нескольких факторных признаков. Множественная модель регрессии имеет вид: 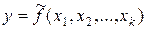
1.9.4.1 Парная регрессия. Парная корреляция
Если предполагается, что величина результативного признака 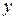 сложилась, в основном, под влиянием лишь одного факторного признака
сложилась, в основном, под влиянием лишь одного факторного признака 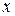 , при исследовании взаимосвязей между ними используют парную модель функции регрессии.
, при исследовании взаимосвязей между ними используют парную модель функции регрессии.
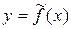 (9.19)
(9.19)
Для того чтобы, построить парную корреляционно-регрессионную модель необходимо решить следующие задачи:
1. отбор фактора,
2. спецификация модели (выбор вида функции регрессии).
Отбор фактора в модель парной регрессии
Фактор, который будет использован в парной модели, должен отвечать следующим требованиям: его влияние на результат должно быть таким, что влиянием всех остальных факторов можно пренебречь, но он не должен находиться в функциональной зависимости с результатом.
Число наблюдений фактора 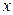 должно превышать число параметров при переменной
должно превышать число параметров при переменной 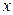 в 6-7 раз. Так для модели вида
в 6-7 раз. Так для модели вида 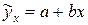 необходимо не менее 6-7 наблюдений, а для модели
необходимо не менее 6-7 наблюдений, а для модели 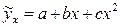 потребуется не менее 12-14 наблюдений.
потребуется не менее 12-14 наблюдений.
Спецификация модели парной регрессии
В парной регрессии используют линейные и нелинейные функции:
· 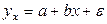 – линейная функция
– линейная функция
· 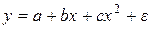 – полином второй степени
– полином второй степени
· 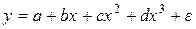 – полином третьей степени и т.д.
– полином третьей степени и т.д.
· 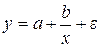 – равносторонняя гипербола
– равносторонняя гипербола
· 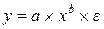 – степенная функция
– степенная функция
· 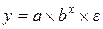 – показательная функция и т.д.
– показательная функция и т.д.
Выбор вида функции в модели парной регрессии может быть осуществлен следующими методами:
1. Графический метод. В его основу положено построение и исследование графика «корреляционное поле», на основании которого делается вывод о виде функции описывающей взаимосвязь между явлениями.
2. Аналитический метод. Опирается на изучение природы взаимосвязи между исследуемыми явлениями.
3. Экспериментальный метод. Вид функции подбирается экспериментально через анализ качества подбора функции, путем сравнения остаточной дисперсии рассчитанной для разных моделей.
1.9.4.1.1 Парная линейная регрессия
Парная линейная регрессия наиболее часто применяется в регрессионных моделях, в силу простоты расчета и интерпретирования результатов.
Расчет регрессионной модели данного вида заключается в нахождении уравнения вида:
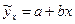 (9.20)
(9.20)
или 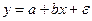 (9.21)
(9.21)
где;
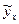 - теоретическое значение результативного признака, рассчитанное по уравнению регрессии, показывающему взаимосвязь между
- теоретическое значение результативного признака, рассчитанное по уравнению регрессии, показывающему взаимосвязь между 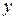 и
и 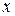 .
.
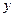 - фактическое значение результативного признака.
- фактическое значение результативного признака.
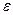 - случайная величина (возмущение, шум)
- случайная величина (возмущение, шум)
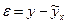 (9.22)
(9.22)
Показывает влияние не учтенных в модели факторов, а также случайных ошибок.
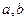 - параметры уравнения.
- параметры уравнения.
Решение уравнения регрессии заключается в расчете его параметров. Наибольшее распространение из методов расчета параметров уравнения получил метод наименьших квадратов (МНК). МНК позволяет получать такие значения 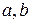 , которые минимизируют сумму квадратов отклонений фактических значений
, которые минимизируют сумму квадратов отклонений фактических значений 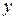 от теоретических
от теоретических 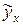 .
.
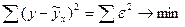 (9.23)
(9.23)
При расчете параметров уравнения при помощи МНК необходимо решить систему из двух нормальных уравнений.
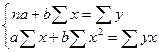 (9.24)
(9.24)
Также используют и готовые уравнения.
Для расчета параметра 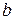 :
:
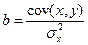 ; так как
; так как 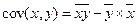 получим:
получим:
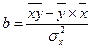 или
или 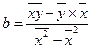 (9.25)
(9.25)
где: 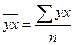 (9.26)
(9.26)
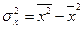 (9.27)
(9.27)
Для расчета параметра 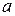 :
:
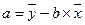 (9.28)
(9.28)
Параметр 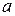 - это теоретическое значение результативного признака
- это теоретическое значение результативного признака 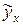 при
при 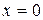 и только в этом случае имеет экономический смысл, если
и только в этом случае имеет экономический смысл, если 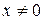 параметр
параметр 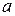 экономического смысла не имеет. В геометрическом представлении означает координату точки пересечения линии регрессии
экономического смысла не имеет. В геометрическом представлении означает координату точки пересечения линии регрессии 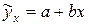 с осью ординат.
с осью ординат.
Параметр 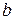 называется коэффициентом регрессии. Коэффициент регрессии показывает, на сколько единиц, в среднем изменится результативный признак, если факторный признак увеличится на одну единицу. Например, если уравнение регрессии имеет вид:
называется коэффициентом регрессии. Коэффициент регрессии показывает, на сколько единиц, в среднем изменится результативный признак, если факторный признак увеличится на одну единицу. Например, если уравнение регрессии имеет вид:
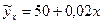
где 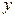 прибыль млн. руб. в месяц, а
прибыль млн. руб. в месяц, а 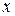 затраты на маркетинг тыс. руб. в месяц. Можно сказать, что при дополнительных затратах на маркетинг на 1 тыс. руб. прибыль в среднем возрастет на 0,02 млн. руб.
затраты на маркетинг тыс. руб. в месяц. Можно сказать, что при дополнительных затратах на маркетинг на 1 тыс. руб. прибыль в среднем возрастет на 0,02 млн. руб.
Геометрически это тангенс угла наклона прямой регрессии 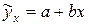 .
.
1.9.4.1.2 Парная линейная корреляция
Простейшим методом определения наличия и формы взаимосвязи является построения корреляционной таблицы и графика «корреляционное поле».
Корреляционная таблица – таблица, в которой записываются частоты сочетаний результативного и факторного показателей. В настоящее время корреляционная таблица не используется для вычисления уравнения связи.
По корреляционной таблице можно сделать следующие выводы. Если 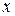 и
и 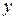 распложены по возрастанию, то расположение частот около диагонали таблицы слева вниз направо говорит о прямой форме связи, если по диагонали вверх направо, то связь обратная. Если частоты находятся равномерно по всей таблицы – связь слабая.
распложены по возрастанию, то расположение частот около диагонали таблицы слева вниз направо говорит о прямой форме связи, если по диагонали вверх направо, то связь обратная. Если частоты находятся равномерно по всей таблицы – связь слабая.
Корреляционное поле (графический метод изучения взаимосвязей) – точечный график, характеризующий единицу наблюдения по двум признакам. Факторный признак откладывается по оси абсцисс, результативный признак по оси ординат.
По данным примера 8 построим корреляционное поле (рис. 9.4).
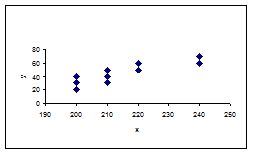
Рисунок 9.4
Анализ корреляционного поля показывает, что имеется прямая связь.
Если связь между признаками обратная, то корреляционное поле будет иметь примерно такой вид (рис. 9.5).
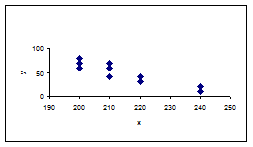
Рисунок 9.5
Если корреляционное поле имеет следующий вид (рис. 6) можно сделать вывод об отсутствии выраженной взаимосвязи.
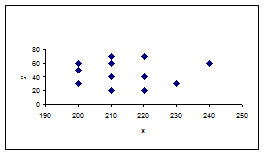
Рисунок 9.6
Корреляционная таблица и корреляционное поле показывают лишь наличие, отсутствие и направление связи. Но они не дают представления о тесноте, интенсивности связи между признаками.
Тесноту связи в парной линейной модели определяют, рассчитывая линейный коэффициент парной корреляции 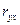 или просто коэффициент корреляции. Существуют формулы расчета:
или просто коэффициент корреляции. Существуют формулы расчета:
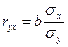 (9.29)
(9.29)
или 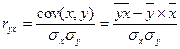 (9.30)
(9.30)
где: 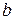 - коэффициент регрессии;
- коэффициент регрессии;
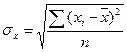 - среднее квадратическое значение факторного признака;
- среднее квадратическое значение факторного признака;
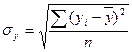 - среднее квадратическое значение результативного признака;
- среднее квадратическое значение результативного признака;
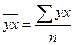
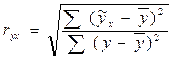 (9.31)
(9.31)
где 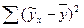 - сумма квадратов отклонений обусловленная влиянием фактора
- сумма квадратов отклонений обусловленная влиянием фактора 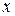 ;
;
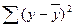 - общая сумма квадратов отклонений признака
- общая сумма квадратов отклонений признака 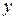 .
.
Коэффициент корреляции также можно рассчитать через значение признаков в стандартизованном масштабе:
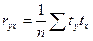 (9.32)
(9.32)
где: 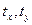 – значения признаков в стандартизованном масштабе.
– значения признаков в стандартизованном масштабе.
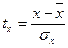 (9.33)
(9.33)
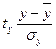 (9.34)
(9.34)
Коэффициент корреляции может принимать значения от 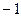 до
до 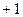 . В статистике говорят, что если значения коэффициента парной корреляции:
. В статистике говорят, что если значения коэффициента парной корреляции:
· меньше 0,3 (-0,3) - связь положительная (отрицательная) слабая;
· от 0,3 до 0,7 (от -0,3 до -0,7) - связь положительная (отрицательная) средняя;
· свыше 0,7 (-0,7) - связь положительная (отрицательная) сильная;
· равен 1 (-1) - связь функциональная положительная (отрицательная);
· равен 0 – связь отсутствует.
Другой показатель тесноты связи – коэффициент парной детерминации. Он показывает часть вариации результативного признака, которая сложилась под влиянием включенного в парную модель фактора. Коэффициент парной детерминации 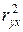 рассчитывают, возводя в квадрат коэффициент парной корреляции
рассчитывают, возводя в квадрат коэффициент парной корреляции 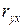 или по формуле:
или по формуле:
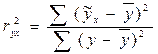 (9.35)
(9.35)
Коэффициент парной детерминации позволяет определять тесноту связи не только в линейных, но и в нелинейных моделях.
Коэффициент парной детерминации может принимать значения от 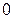 до
до 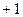 .
.
1.9.4.1.3 Оценка надежности уравнения парной линейной регрессии, его параметров и коэффициента парной линейной корреляции
Результаты корреляционно-регрессионного анализа необходимо проверить, проведя оценку существенности, как уравнения регрессии, так и его параметров и коэффициента корреляции.
Оценка существенности уравнения регрессии в целом проводится с помощью критерия Фишера – F-критерия.
При этом исходят из представления, что если между изучаемыми признаками 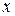 и
и 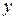 есть связь и уравнение парной линейной регрессии эту связь отражает, то вариация результативного признака
есть связь и уравнение парной линейной регрессии эту связь отражает, то вариация результативного признака 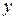 , обусловленная влиянием факторного признака
, обусловленная влиянием факторного признака 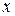 (факторная вариация) должна быть в несколько раз больше, чем вариация результативного признака, вызванная всеми другими факторами (остаточная вариация).
(факторная вариация) должна быть в несколько раз больше, чем вариация результативного признака, вызванная всеми другими факторами (остаточная вариация).
Для этого вначале проводят исследование дисперсии.
Общую сумму квадратов отклонений раскладывают на две части – «факторную» и «остаточную».
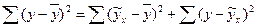 (9.36)
(9.36)
где: 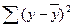 - общая сумма квадратов отклонений;
- общая сумма квадратов отклонений;
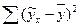 - факторная сумма квадратов отклонений;
- факторная сумма квадратов отклонений;
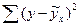 - остаточная сумма квадратов отклонений.
- остаточная сумма квадратов отклонений.
Разделив каждую сумму квадратов отклонений на соответствующее число степеней свободы ( 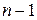 для общей суммы,
для общей суммы, 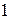 для факторной и
для факторной и 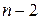 для остаточной) получим дисперсию на одну степень свободы -
для остаточной) получим дисперсию на одну степень свободы - 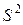 .
.
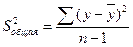 (9.37)
(9.37)
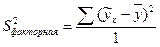 (9.38)
(9.38)
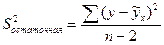 (9.39)
(9.39)
Для расчета F-критерия сопоставим факторную и остаточную дисперсию;
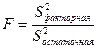 (9.40)
(9.40)
Также F-критерий можно рассчитать по формуле:
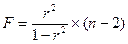 (9.41)
(9.41)
Оценку существенности уравнения регрессии проводят, сравнивая полученное значение F-критерия ( 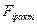 ) с табличным значением (
) с табличным значением ( 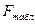 ), которое берут из таблиц критических значений F-отношений при определенном уровне значимости, как правило:
), которое берут из таблиц критических значений F-отношений при определенном уровне значимости, как правило: 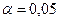 или
или 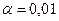 , и числе свободы:
, и числе свободы: 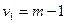 ,
, 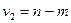 (таблицы Снедекора-Фишера – приложение 2).
(таблицы Снедекора-Фишера – приложение 2).
Если 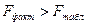 то уравнение регрессии значимо, если меньше незначимо.
то уравнение регрессии значимо, если меньше незначимо.
Значимость параметров уравнения 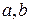 и коэффициента корреляции
и коэффициента корреляции 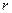 проверяют при помощи критерия Стьюдента – t-критерия.
проверяют при помощи критерия Стьюдента – t-критерия.
Критерий Стьюдента для коэффициента регрессии 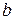 рассчитывается как;
рассчитывается как;
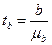 (9.42)
(9.42)
где; 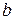 - коэффициент регрессии.
- коэффициент регрессии.
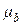 - стандартная ошибка коэффициента регрессии, рассчитывается как:
- стандартная ошибка коэффициента регрессии, рассчитывается как:
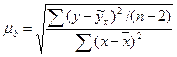 (9.43)
(9.43)
Учитывая, что 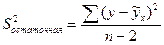
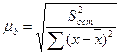 (9.44)
(9.44)
Критерий Стьюдента для параметра 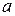 рассчитывается как;
рассчитывается как;
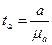 (9.45)
(9.45)
где: 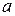 - свободный член уравнения регрессии.
- свободный член уравнения регрессии.
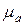 - стандартная ошибка параметра
- стандартная ошибка параметра 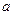 , рассчитывается как:
, рассчитывается как:
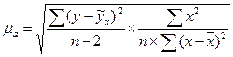 (9.46)
(9.46)
или 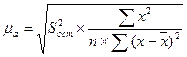 (9.47)
(9.47)
Критерий Стьюдента для коэффициента корреляции 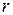 рассчитывается как;
рассчитывается как;
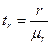 (9.48)
(9.48)
или 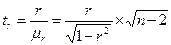 (9.49)
(9.49)
где: 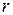 - коэффициент парной линейной корреляции.
- коэффициент парной линейной корреляции.
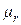 - стандартная ошибка коэффициента корреляции, рассчитывается как:
- стандартная ошибка коэффициента корреляции, рассчитывается как:
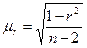 (9.50)
(9.50)
Кроме того, для парной линейной регрессии верно, что:
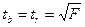 (9.51)
(9.51)
Полученные фактические значения критерия Стьюдента сравнивают с табличными значениями при определенном уровне значимости 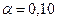 ,
, 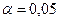 или
или
