Расчет показателей безотказности восстанавливаемых элементов ЭУ

Восстанавливаемыми объектом называется такой объект, который в случае возникновения дефекта может быть восстановлен (дефект устранен). При этом могут рассматриваться следующие случаи.

Случай 1. Резервирование с восстановлением (отказавшие элементы ремонтируются и включаются в состав резерва). При этом ремонт осуществляется во время функционирования ЭУ. В этом случае при резервировании одним элементом отказ ЭУ произойдет только в том случае, когда откажут два элемента, и к моменту отказа второго блока первый еще не будет восстановлен. В этом случае при проектировании должно удовлетворяться условие <Тср, где – время восстановления отказавшего элемента; Т_ср – время безотказной работы.

Случай 2. Основное соединение элементов в ЭУ при условии, что выходные параметры выделяются дискретно и используются за время, необходимое для выработки новых данных. В этом случае при проектировании ЭУ необходимо обеспечить условие <t_у, где – время восстановления отказавших элементов; t_у – время устаревания выходных параметров, выдаваемых дискретно.

Случай 3. ЭУ выполняет поставленные задачи в том случае, если дефект отсутствует в ней к началу применения и не возникает за время t выполнения задачи, а также будет восстановлен за время <t и не откажет за время (t- ), которое достаточно для выполнения задачи. При этом проектируемая ЭУ должна удовлетворять следующему условию: <t- , где t – время, требуемое для выполнения задачи. Для этого случая t разделяют на две части: первый участок, когда отказ ЭУ допустим при условии <t- , и второй, когда отказ ЭУ недопустим, т.к. в этом случае не будет решена поставленная задача.

Вероятность того что задача будет выполнена, определяется по формуле полной вероятности сложного события:

,

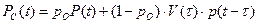где 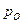– вероятность отсутствия дефекта перед применением ЭУ; Р(t) – вероятность безотказной работы за время t; 1-р_о – вероятность наличия дефекта в ЭУ перед применением; V( ) - вероятность восстановления и проверки ЭУ к моменту времени <t; р(t- ) – вероятность безотказной работы ЭУ за время (t- ), достаточное для решения задачи.

В том случае, когда время безотказной работы значительно больше времени восстановления, вероятность безотказной работы можно рассчитывать по формуле:

,

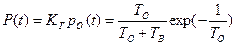где Т_в – среднее время восстановления работоспособности.

Если предположить, что имеет место простейший закон распределения отказов элементов, то вероятность безотказной работы для любого момента времени можно определить из следующей системы уравнений:

;

,

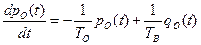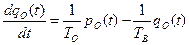где 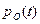– вероятность безотказной работы в любой момент времени; 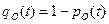– вероятность неработоспособного состояния ЭУ.

Для решения системы уравнений (3.9) в качестве начального условия примем, что при t=0 0< 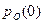<1, т.е. отлично от единицы. При этих начальных условиях и с учетом того, что 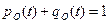, т.е. имеет место полная группа событий, решение системы уравнений (3.9) будет иметь вид:

.

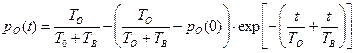Из этого выражения следует, что при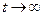

.

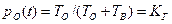Рассмотрим два крайних случая:

1. 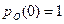и 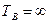– в начальный момент времени вероятность безотказной работы равна единице и после отказа ЭУ не восстанавливается. В этом случае 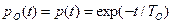, т.е. следует рассматривать вероятность до возникновения первого отказа.

2. 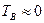– отказавший элемент моментально заменяется резервным. В этом случае в соответствии с (3.10) .

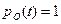Таким образом, вероятность безотказной работы, характеризующая надежность восстанавливаемой ЭУ, ограничена крайними значениями, которые соответствуют двум предельным значениям среднего времени восстановления Т_в.

Примеры расчета показателей безотказности