Дифференциальные уравнения в частных производных.
1.Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную 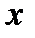 , искомую функцию
, искомую функцию 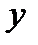 и ее производные или дифференциалы. Символически дифференциальное уравнение записывается так:
и ее производные или дифференциалы. Символически дифференциальное уравнение записывается так:
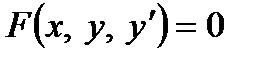 ,
, 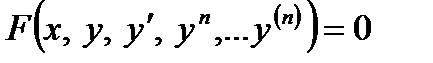
Дифференциальным уравнением называется обыкновенным, если искомая функция зависит от одного независимого переменного.
Порядком дифференцированного уравнения называется порядок старшей производной (или дифференциала), входящей в данное уравнение.
Решением (или интегралом) дифференцированного уравнения называется такая функция, которая обращает это уравнение в тождество.
Общим решением (или общим интегралом) дифференцированного уравнения называется такое уравнения, в которое входит столько независимых производных постоянных, каков порядок уравнения. Так, общее решение дифференцированного уравнения первого порядка содержит одну произвольную постоянную.
Частным решением дифференциального уравнения называется решение, полученное из общего при различных числовых значениях произвольных постоянных. Значение произвольных постоянных находятся при предельных начальных значениях аргумента и функции. График частного решения дифференциального уравнения называется интегральной кривой.
Общему решению дифференциального уравнения соответствует совокупность (семейство) всех интегральных кривых.
Дифференциальным уравнением первого порядка называется уравнение в которое входят производные (или дифференциалы) не выше первого порядка.
Дифференциальным уравнением с разделяющимися переменными 1-го порядка называется уравнение вида: 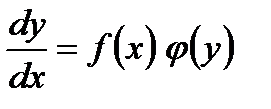
Для решения этого уравнения нужно сначала разделить переменные: 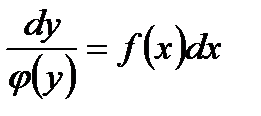
А затем проинтегрировать обе части полученного равенства:
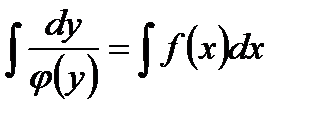
Уравнение вида: 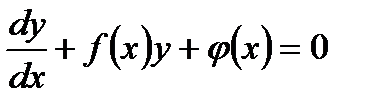 , где
, где 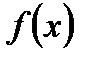 и
и 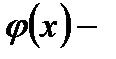 функции от
функции от 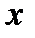 , называется линейным дифференциальным уравнением первого порядка. В частном случае
, называется линейным дифференциальным уравнением первого порядка. В частном случае 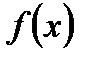 и
и 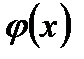 могут быть постоянными величинами. Это уравнение приводится к уравнению с разделяющимися переменными,
могут быть постоянными величинами. Это уравнение приводится к уравнению с разделяющимися переменными, 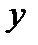 и
и 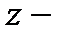 новые функции от
новые функции от 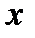 .
.
Т. о. 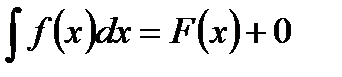 , или
, или 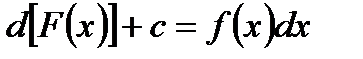
Здесь 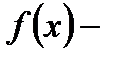 подинтегральная функция,
подинтегральная функция, 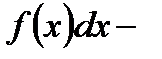 подинтегральное выражение, с – произвольная постоянная.
подинтегральное выражение, с – произвольная постоянная.
1.Найти общее решение уравнения
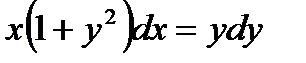
Решение: Разделить переменные, имеем: 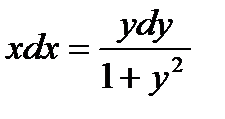
Интегрируем обе части полученного уравнения:
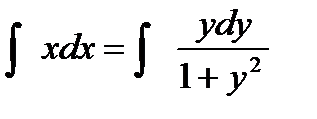
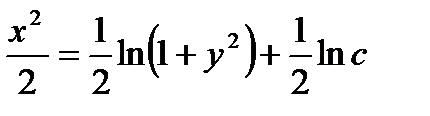
Т. к. произвольная постоянная с может принимать любые числовые значения, то для удобства дальнейших преобразований вместо с мы напишем 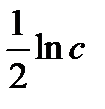 . потенцируя последнее выражение получим
. потенцируя последнее выражение получим 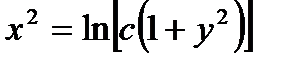 . Это есть общее решение данного уравнения.
. Это есть общее решение данного уравнения.
2.Найти частное решение уравнения 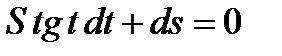 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 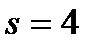 при
при 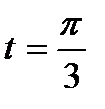
Решение: Разделив переменные, имеем
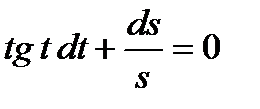
Проинтегрируем обе части полученного уравнения
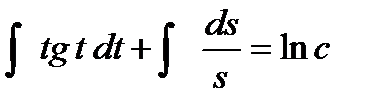
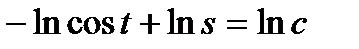 или
или 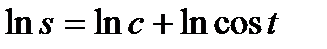
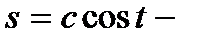 общее решение
общее решение
Используя 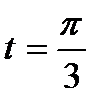 и
и 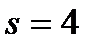 , получим
, получим 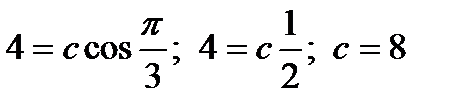
Следовательно, искомое частное решение, удовлетворяющее начальным условиям, имеет вид: 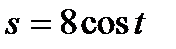
3.Найти общее решение уравнения
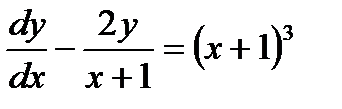
Решение: Это линейное уравнение: здесь 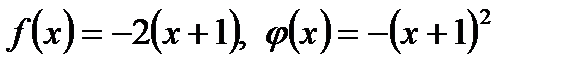
Положим 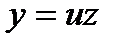 и продифференцируем это равенство по
и продифференцируем это равенство по 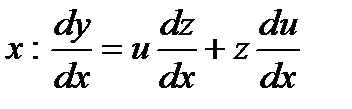 . Подставив теперь выражение для у и
. Подставив теперь выражение для у и 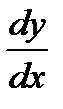 в данное уравнение, получим
в данное уравнение, получим
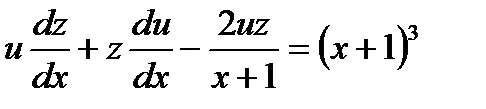 или
или 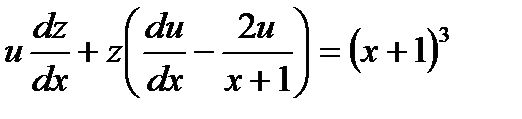
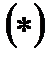
Т. к. одну из вспомогательных функций 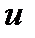 или
или 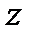 можно выбрать произвольно, то в качестве
можно выбрать произвольно, то в качестве 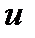 возьмем одно из частных решений уравнения
возьмем одно из частных решений уравнения 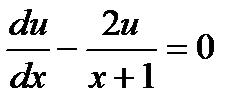 разделив в этом уравнении переменные и интегрируя, имеем:
разделив в этом уравнении переменные и интегрируя, имеем:
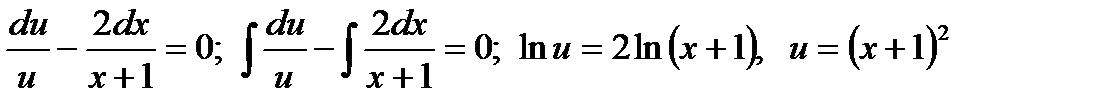
(произвольную постоянную с примем = 0, т. к. находим одно из частных решений) подставим теперь выражение для 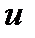 в уравнение
в уравнение 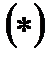 ; тогда получим уравнение:
; тогда получим уравнение:
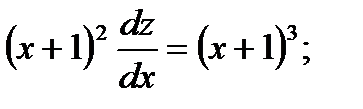 или
или 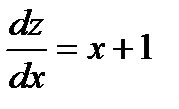
Отсюда находим: 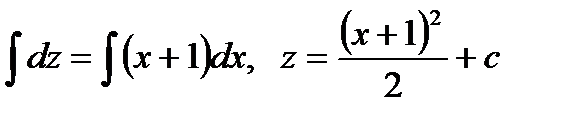
Зная 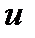 и
и 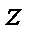 получим общее решение:
получим общее решение:
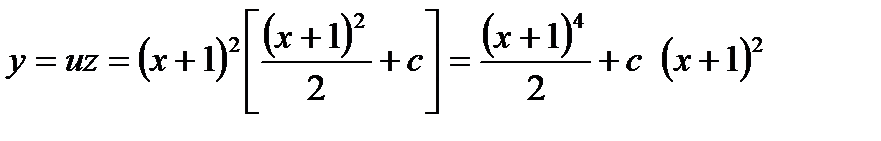
2.Уравнения, содержащие производные (или дифференциалы) не выше второго порядка, называются дифференциальными уравнениями второго порядка. Общий вид уравнения записывается следующим образом 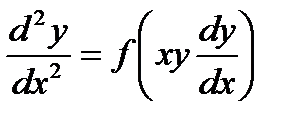 или
или 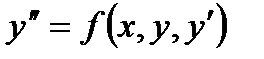
Общее решение дифференциального уравнения второго порядка содержит две произвольные постоянные.
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называются уравнения вида:
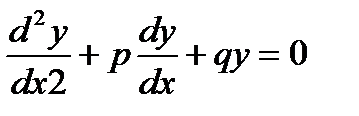 где
где 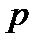 и
и 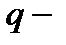 постоянные величины
постоянные величины
Для нахождения общего решения составляется характеристическое уравнение:
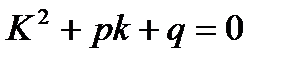 , где
, где 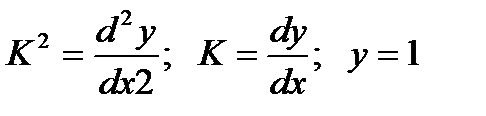
Решив, полученное уравнение находим 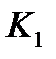 и
и 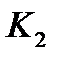 . Зависимости от
. Зависимости от 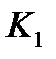 и
и 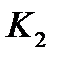 возможны случаи:
возможны случаи:
1) Если корни 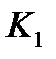 и
и 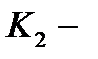 действительные и различные, то решение уравнения имеет вид:
действительные и различные, то решение уравнения имеет вид: 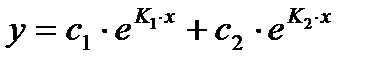
2) Если корни 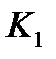 и
и 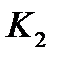 равны, то общее решение имеет вид:
равны, то общее решение имеет вид: 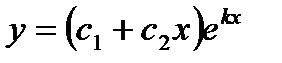
3) Если корни 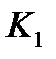 и
и 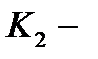 комплексно-сопряженные, т. е. Уравнения, содержащие производные (или дифференциалы) не выше второго порядка, называются дифференциальными уравнениями второго порядка. Общий вид уравнения записывается следующим образом:
комплексно-сопряженные, т. е. Уравнения, содержащие производные (или дифференциалы) не выше второго порядка, называются дифференциальными уравнениями второго порядка. Общий вид уравнения записывается следующим образом:
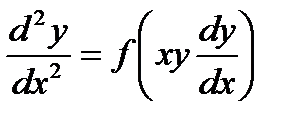 или
или 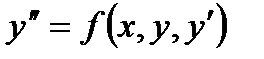
Общее решение дифференциального уравнения второго порядка содержит две произвольные постоянные.
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называются уравнения вида:
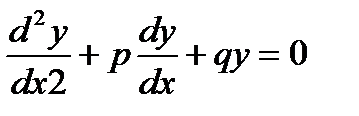 где
где 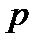 и
и 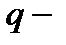 постоянные величины
постоянные величины
Для нахождения общего решения составляется характеристическое уравнение:
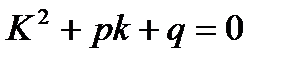 , где
, где 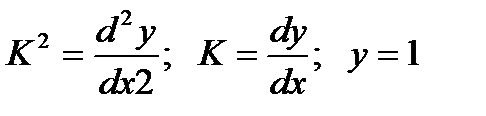
Решив, полученное уравнение находим 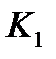 и
и 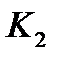 . Зависимости от
. Зависимости от 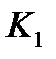 и
и 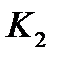 возможны случаи:
возможны случаи:
1) Если корни 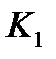 и
и 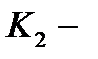 действительные и различные, то решение уравнения имеет вид:
действительные и различные, то решение уравнения имеет вид: 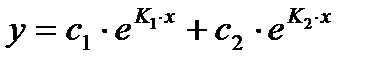
2) Если корни 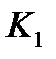 и
и 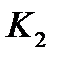 равны, то общее решение имеет вид:
равны, то общее решение имеет вид: 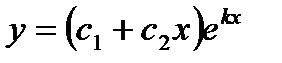
3) Если корни 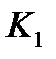 и
и 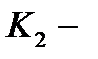 комплексно-сопряженные, т. е.
комплексно-сопряженные, т. е. 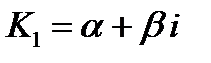 и
и 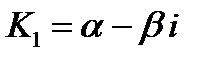
То общее решение имеет вид: 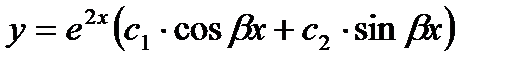
1.Найти общее решение уравнения 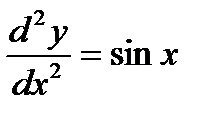
Это неполное дифференциальное уравнение 2-го порядка вида 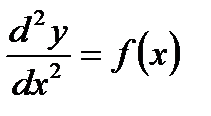 . Полагаем
. Полагаем 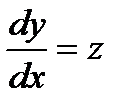 ; тогда данное уравнение можно записать в виде
; тогда данное уравнение можно записать в виде 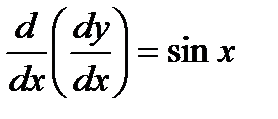 , т. е.
, т. е. 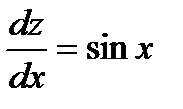 откуда
откуда 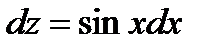 Интегрируя равенство, получим
Интегрируя равенство, получим 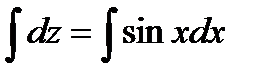 т. е.
т. е.
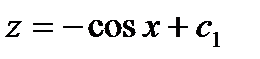 Следовательно,
Следовательно, 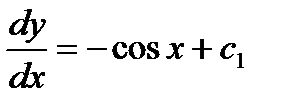 , т. е.
, т. е.
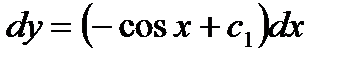 Снова интегрируя, находим
Снова интегрируя, находим
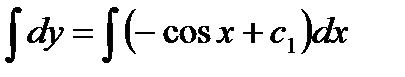 , или
, или 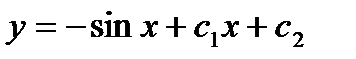 . Это и есть общее решение данного уравнения.
. Это и есть общее решение данного уравнения.
2.Найти частное решение уравнения 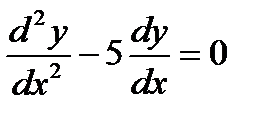 , если
, если 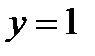 и
и 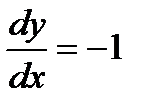 при
при 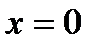 . Составим характеристическое уравнение
. Составим характеристическое уравнение 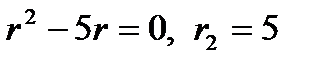 . Так как корни характеристического уравнения действительные и различные, то общее решение дифференциального уравнения имеет вид
. Так как корни характеристического уравнения действительные и различные, то общее решение дифференциального уравнения имеет вид 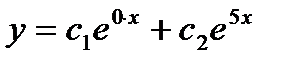 т. е.
т. е. 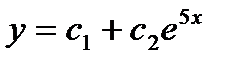
Для нахождения искомого частного решения значение 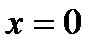 ,
, 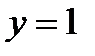 , получим
, получим 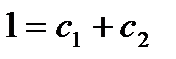 . Продифференцировав общее решение и подставив в полученное выражение значения
. Продифференцировав общее решение и подставив в полученное выражение значения 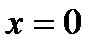 ,
, 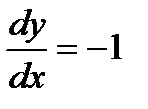 , имеем
, имеем 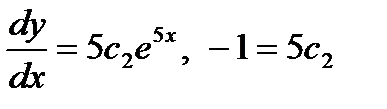 . Отсюда находим:
. Отсюда находим:
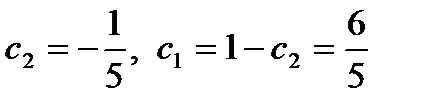 . Таким образом, искомое частное решение имеет вид
. Таким образом, искомое частное решение имеет вид 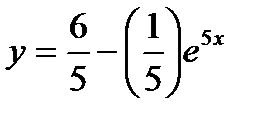
3.Решить уравнение 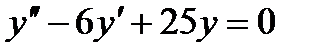
Составим характеристическое уравнение и найдем его корни: 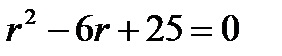 ;
; 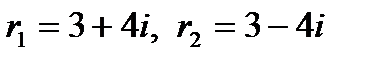 ; здесь
; здесь 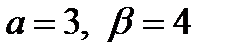 . Так как характеристическое уравнение имеет два комплексно – сопряженных корня, то общее решение дифференциального уравнения согласно формуле:
. Так как характеристическое уравнение имеет два комплексно – сопряженных корня, то общее решение дифференциального уравнения согласно формуле: 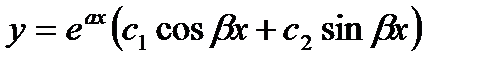 записывается в виде
записывается в виде 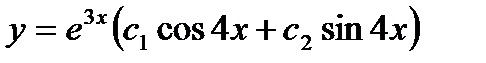
Вопросы для самопроверки:
1.Какое уравнение называют дифференциальным уравнением? Приведите примеры.
2.Если искомая функция зависит от одного независимого переменного, то как называют такое дифференциальное уравнение?
3.Какие из следующих уравнений являются дифференциальными: 1) 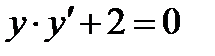 ; 2)
; 2) 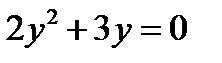 ; 3)
; 3) 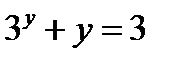 ; 4)
; 4) 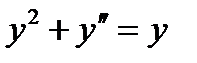 ; 5)
; 5) 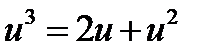 ?
?
4.Что называют порядком дифференциального уравнения?
5.Какая функция называется решением (или интегралом) дифференциального уравнения?
6.Какое уравнение называют общим решением (или общим интегралом) дифференциального уравнения?
7. Какое решение называют частным решением дифференциального уравнения?
8.Какое уравнение называют дифференциальным уравнением с разделяющимися переменными?
9.Каков геометрический смысл общего и частного решений дифференциального уравнения?
10.Может ли дифференциальное уравнение иметь конечное число решений?
11.Сколько постоянных интегрирования имеет общее решение дифференциального уравнения первого порядка?
12.Как проверить, правильно ли найдено решение дифференциального уравнения?
13.Какое уравнение называют дифференциальным уравнением 2-го порядка?
14. Какой вид имеет дифференциальное уравнение 2-го порядка?
15. Сколько произвольных постоянных содержит общее решение дифференциального уравнения 2-го порядка?
16. Как определяется и как записывается в общем виде линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами.
17. Какое уравнение составляется для отыскания общего решения линейного однородного дифференциального уравнения?
18. Опишите возможные случаи общего решения дифференциального уравнения.
19.Что такое характеристическое уравнение?
