Линейные неоднородные дифференциальные уравнения первого порядка

Определение 5.1 .Дифференциальное уравнение вида

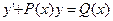(5.1)

называется линейнымнеоднородным дифференциальным уравнением первого порядка относительно переменной 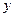, а уравнение

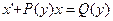(5.1 )

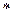называется линейнымнеоднородным дифференциальным уравнением первого порядка относительно переменной .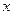

При 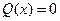уравнение 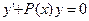(5.2)

называется линейнымоднородным дифференциальным уравнением первого порядка и является уравнением с разделяющимися переменными.

Его общее решение имеет вид: 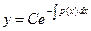, (5.3)

где С=const.

Аналогично для уравнения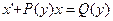

Решение линейного однородного дифференциального уравнения первого порядка (5.1) можно найти методом вариации производной постоянной или методом Бернулли.

Метод вариации произвольной постоянной.

Определим общее решение уравнения (5.2)-соответствующего однородного уравнения (5.1): .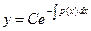

Решение линейного неоднородного дифференциального уравнения (5.1) будем искать в виде

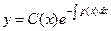, (5.4)

считая 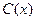-некоторой функцией переменной .

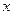Подставляя 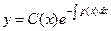и

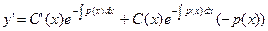в (5.1),получим дифференциальное уравнение первого порядка с разделяющимися переменными , из которого найдем :

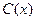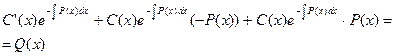
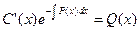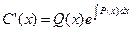
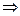
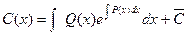; , (5.5)

где .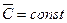

Подставив (5.5) в (5.4) получим общее решение уравнения (5.1)

Пример 5.1Решить задачу Коши ; .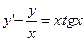

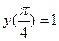Решение. 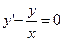- однородное линейное дифференциальное уравнение первого порядка.

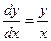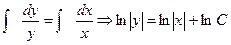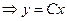; ; - общее решение линейного однородного уравнения.

Найдем общее решение линейного неоднородного уравнения в виде 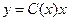и подставим в неоднородное линейное дифференциальное уравнение первого порядка 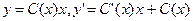.Найдем :

; ;

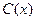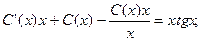
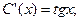
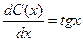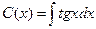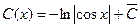
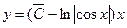- общее решение линейного неоднородного уравнения. Найдем частное решение.

, ,

, ,

, .

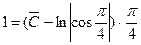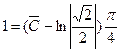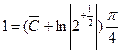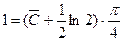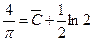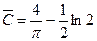Тогда 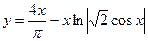- частное решение линейного неоднородного уравнения.

Метод Бернулли.

Общее решение линейного неоднородного уравнения первого порядка (5.1) будем искать в виде 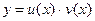(5.6),

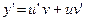или ( 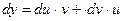) (5.7)

Подставим (5.6) в (5.1).Получим

.

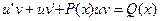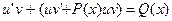
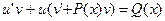
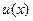Так как и 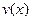произвольные ненулевые функции, произведение которых дает функцию 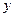,то выберем их так ,чтобы выражение в скобках обращалось в ноль.

Тогда система 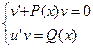будет равносильна уравнению (5.1)

Решение первого уравнения с разделяющимися переменными 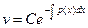, подставляется во второе уравнение. При этом С берется произвольным, т.к. нас интересует любая одна функция , обращающая в ноль выражение в скобках.

Решение первого и второго уравнения подставляем в (5.6), которое служит решением исходного уравнения (5.1)

Пример 5.2.

Найти частное решение уравнения , .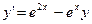

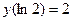Решение: Определим тип уравнения:

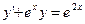-линейное неоднородное уравнение первого порядка,

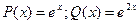
Решим его методом Бернулли .Общее решение будем искать в виде .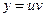

,

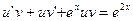
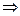
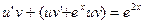
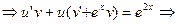
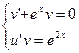решим первое -уравнение с разделяющимися переменными

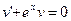
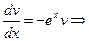
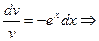
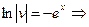
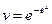.Подставим во второе уравнение.

;

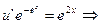
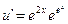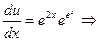
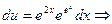
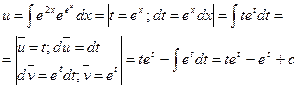
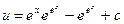
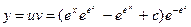общее решение уравнения .

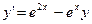Найдем частное решение ,удовлетворяющее начальным условиям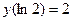

; ;

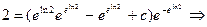
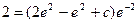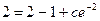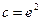
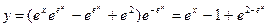частное решение уравнения 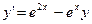, удовлетворяющее начальным условиям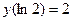

Определение 5.2Дифференциальное уравнение вида

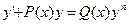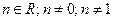, (5.8)

называется уравнением Бернулли. Оно сводится к линейному неоднородному дифференциальному уравнению первого порядка заменой переменных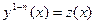

Пример 5.3.

Найти частное решение уравнения Бернулли

,

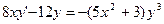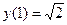
Решение: Преобразуем уравнение к виду , разрешенному относительно первой производной ; ;

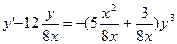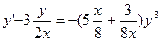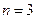
Поделим обе части уравнения на 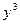, считая 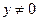, и введем новую переменную

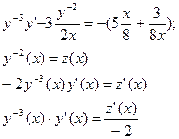
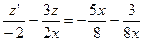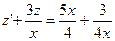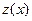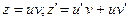
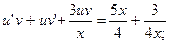
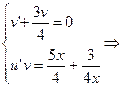
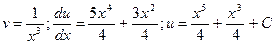
или -линейное уравнение относительно функции .Решим его методом Бернул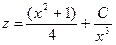ли.

или 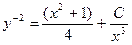,тогда 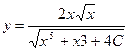- общее решение.

Найдем частное решение:

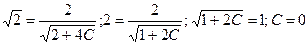
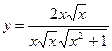или 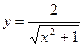-частное решение уравнения 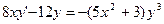,удовлетворяющее начальным условиям

.
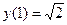