Лекция 9. Линейные операции над векторами в координатах
Скалярное произведение векторов
Пусть точки 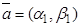 ,
, 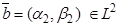 . Тогда длина отрезка, соединяющего концы векторов
. Тогда длина отрезка, соединяющего концы векторов 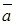 ,
, 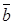 , находится по очевидной формуле:
, находится по очевидной формуле: 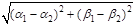 . Для расстояния
. Для расстояния 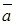 от начала
от начала 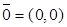 введем обозначения
введем обозначения 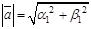 . Перейдем к углам между векторами. Если j - угол между отрезком, соединяющим О с
. Перейдем к углам между векторами. Если j - угол между отрезком, соединяющим О с 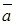 и положительной осью a1, а
и положительной осью a1, а 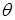 - угол между отрезком, соединяющим О с
- угол между отрезком, соединяющим О с 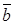 и той же осью, то углом между векторами
и той же осью, то углом между векторами 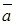 и
и 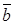 будет
будет 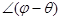 . Тогда
. Тогда 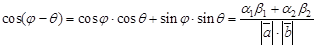 . Введем обозначение:
. Введем обозначение: 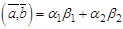 .
.
Определение.Скалярным произведением 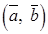 ненулевых векторов
ненулевых векторов 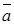 и
и 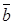 называется число, равное произведению их модулей на косинус угла между ними, то есть
называется число, равное произведению их модулей на косинус угла между ними, то есть 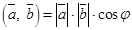 .
.
Если хотя бы один из векторов 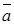 и
и 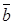 нулевой, то скалярное произведение равно нулю. Для обозначения скалярного произведения часто используется запись
нулевой, то скалярное произведение равно нулю. Для обозначения скалярного произведения часто используется запись 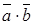 .
.
Из определения следует, что скалярное произведение ненулевых векторов равно нулю тогда и только тогда, когда векторы ортогональны (угол между ними 90°, а 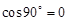 ).
).
Свойства скалярного произведения:
1) 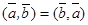 ; 2)
; 2) 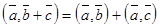 ;
;
3) 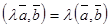 ; 4)
; 4) 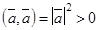 при
при 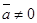 ;
;
5) скалярное произведение двух векторов, заданных декартовыми прямоугольными координатами, равно сумме произведений одноименных декартовых координат, то есть, если 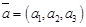 и
и 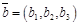 , то
, то 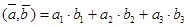 .
.
Скалярное произведение вектора на себя есть квадрат длины самого вектора, а длина вектора из ортонормированного базиса равна единице.
С помощью скалярного произведения находят:
1. длину вектора 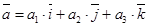 :
: 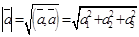 ;
;
2. расстояние d между точками А(х1,у1,z1) и В(х2,у2,z2):
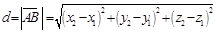 ;
;
3. проекцию одного вектора 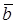 на направление другого вектора
на направление другого вектора 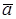 :
: 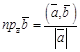 ;
;
4. косинус угла между векторами: 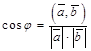 , где j - угол между векторами
, где j - угол между векторами  и
и  ;
;
5. координаты орта вектора  , то есть координаты вектора, направленного так же, как
, то есть координаты вектора, направленного так же, как  , но по длине равного единице. Координаты орта вектора совпадают с его направляющими косинусами:
, но по длине равного единице. Координаты орта вектора совпадают с его направляющими косинусами: 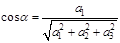 ,
, 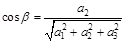 ,
, 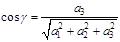 .
.
Векторное и смешанное произведение векторов
Определение.Векторным произведением двух непараллельных векторов  и
и  называется третий вектор
называется третий вектор 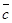 , обозначаемый
, обозначаемый 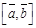 или
или 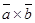 и удовлетворяющий следующим условиям:
и удовлетворяющий следующим условиям:
1. вектор 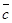 ортогонален каждому из векторов
ортогонален каждому из векторов  и
и  , то есть перпендикулярен плоскости, в которой лежат эти вектора;
, то есть перпендикулярен плоскости, в которой лежат эти вектора;
2. если векторы  ,
,  ,
, 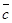 отложены от одной точки О, то с конца вектора
отложены от одной точки О, то с конца вектора 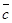 поворот от вектора
поворот от вектора  к вектору
к вектору  на меньший угол осуществляется против часовой стрелки; в этом случае тройка
на меньший угол осуществляется против часовой стрелки; в этом случае тройка  ,
,  ,
, 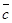 называется правой;
называется правой;
3. 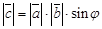 , где
, где 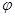 - угол между векторами
- угол между векторами  и
и  ; если векторы
; если векторы  и
и  параллельны, то полагают
параллельны, то полагают 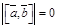 .
.
Свойства векторного произведения:
1. 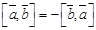 ; 2)
; 2) 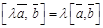 ; 3)
; 3) 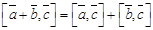 ;
;
2. величина модуля векторного произведения 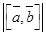 равна площади параллелограмма, построенного на векторах
равна площади параллелограмма, построенного на векторах  и
и  ;
;
3. координаты векторного произведения векторов 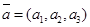 и
и 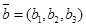 можно найти через определители следующим образом:
можно найти через определители следующим образом: 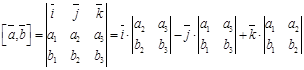 .
.
Определение. Смешанным произведением трех векторов  ,
,  ,
, 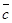 называется скалярное произведение векторного произведения первых двух векторов на третий. Обозначается смешанное произведение следующим образом:
называется скалярное произведение векторного произведения первых двух векторов на третий. Обозначается смешанное произведение следующим образом: 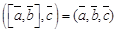 или просто
или просто 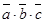 .
.
Свойства смешанного произведения:
1. 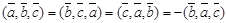 - т.е. перестановка в произведении двух векторов местами ведет к смене знака всего произведения;
- т.е. перестановка в произведении двух векторов местами ведет к смене знака всего произведения;
2. модуль смешанного произведения 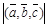 трех некомпланарных векторов равен объёму параллелепипеда, построенного на векторах
трех некомпланарных векторов равен объёму параллелепипеда, построенного на векторах  ,
,  ,
, 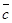 . При этом
. При этом 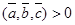 , если тройка
, если тройка  ,
,  ,
, 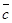 - правая и
- правая и 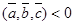 , если тройка векторов левая;
, если тройка векторов левая;
3. если векторы 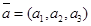 ,
, 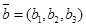 ,
, 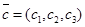 заданы декартовыми координатами, то
заданы декартовыми координатами, то 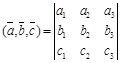 ;
;
4. три векторы  ,
,  ,
, 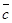 лежат в одной плоскости (компланарны) тогда и только тогда, когда их смешанное произведение равно нулю.
лежат в одной плоскости (компланарны) тогда и только тогда, когда их смешанное произведение равно нулю.
