Корневые методы оценки качества

Поскольку корни ПФ однозначно определяют вид переходного процесса, их можно использовать для оценки: 1) запаса устойчивости и, 2) быстродействия.

Примечание: Обычно обходятся исследованием только полюсов ПФ F(s), т.е. корней характеристического уравнения 1+W(s)=0.

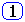Система будет склонна к колебаниям, если имеются комплексные корни вида -a±jb. Оценить эту склонность можно используя показатель запаса устойчивости - колебательность:

m = b/a, 0 < m < ¥

где: a - коэффициент затухания; b - круговая частота колебаний.

Колебательность определяет другой показатель - затухание амплитуды колебаний
x(t) = Ce ^{-a t} sin(bt+j) за период:

.

Задание определенной колебательности заставляет ограничить область расположения корней.

Колебательность системы m можно найти используя подстановку s = z e ^j(90-j), что соответствует повороту осей плоскости корней на угол (90-j). Далее, используя любой критей устойчивости, подбирают угол j, при котором система будет находиться на границе устойчивости. И тогда: m = tg j = b/a.

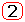Для оценки быстродействия может использоваться понятие степени быстродействия h - это абсолютное значение вещественной части ближайшего к мнимой оси корня. Т.е. если этот корень -a±jb, то h равна коэффициенту затухания a.

И действительно, составляющая в переходном процессе x_h(t) = C_he ^-htsin(bt+j), затухает тем медленней, чем меньше h. Если в конце переходного процесса амплитуда колебаний равна DC_h, то веремя переходного процесса:

.

Задание определенной степени быстродействия заставляет ограничить область расположения корней.

Степень быстродействия h можно найти используя постановку s = z - h_var, что соответствует смещению корней на величину h_var. Далее, используя любой критерий устойчивости, подбирают значение h_var, при котором система будет на границе устойчивости. И тогда: h=h_var.

Понятие о среднегеометрическом корне W₀. Мажоранта и миноранта переходной функции

Пусть имеем характеристическое уравнение:

a₀ s ⁿ + a₁ s ^n-1 + ... + a_n-1 s + a_n = 0 .

Приведем его к нормированному виду (разделим на a_n и выполним подстановку ):

q ⁿ + a₁/a_n (W₀ q) ^n-1 + ... + a_k/a_n (W₀ q) ^n-k +...+ 1 = 0 ,

где: - среднегеометрический корень.

Для статических САР a_n = 1 + K, для астатических a_n = K, a₀ = T₁ T₂ ... T_n; следовательно увеличивая K можно увеличить W₀. На основании теоремы подобия увеличение W₀ вызовет пропорциональное радиальное смещение корней. Т.е. вид переходного процесса меняться не будет, но будет меняться его временной масштаб. Поэтому среднегеометрический корень W₀ является мерой быстродействия.

Для приведенного уравнения время будет безразмерным t = W₀ t, переходная функция h(t) в случае кратных вещественных корней или одной пары комплексных будет ограничена минорантой и мажорантой:

1-u(h, t) < h(t) < 1+u(h, t) ,

где: u(h, t) = e ^-ht [1 + (ht)¹/1! + (ht)²/2! + ... + (ht)^n-1/(n-1)! ] - разложение в ряд Тейлора огибающей той составляющей в пререходном процессе, корень которой ближе к оси "+j".

На рис. демонстрируется, что любой переходный процесс в любой системе будет затухать тем медленней, чем больше корней вблизи оси "+j".