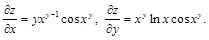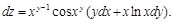Пример 1. Найти область определения функции

.

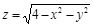Решение.Область определения найдем из неравенства 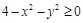, т.е. .

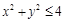Это круг с центром в начале координат с радиусом .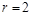

Подобно тому, как функцию 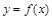изображают графиком, можно геометрически проиллюстрировать уравнение 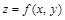. Ставя в соответствие каждой точке 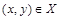аппликату 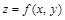, мы получим некоторое множество точек 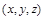в трехмерном пространстве, как правило, некоторую поверхность. Поэтому равенство 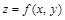называют уравнением поверхности.

3.4.2 Приращение функции 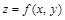. Частные производные и полный дифференциал функции

Понятие непрерывности функции 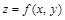аналогично понятию непрерывности для функции одной переменной.

Определение 1.Функция 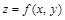называется непрерывной в точке 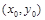, если .

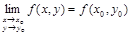Основные свойства непрерывных функций 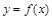справедливы и в кратном случае.

Пусть задана функция 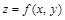и точка .

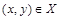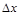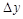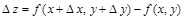Определение 2.Если х получит приращение , а у — приращение , то — называется полным приращением функции.

Если изменение функции z происходит лишь при изменении одного из аргументов х или у, то функция получает частные приращения:

,

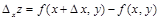или .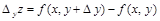

Рассматривая приращение одного аргумента, мы фактически переходим к функции одной переменной.

Определение 3.Если существует конечный предел 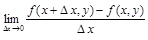, то его называют частной производной функции 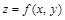по аргументу х и обозначают одним из символов: .

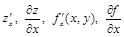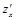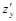Геометрическое содержание и определяется соответствующими касательными к поверхности .

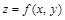Фактически, по определению, каждая частная производная является производной функции одной переменной. Поэтому, при вычислении частных производных можно пользоваться известными правилами и формулами дифференцирования функций одной переменной, считая при этом другую переменную постоянной.

Пример 1. Найти частные производные функций:

а) 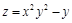; б) .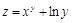

Решение.

а) 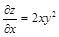(у — фиксированное), 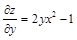(х — фиксированное);

б) 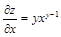, 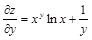(х — фиксированное).

Пример 2. Найти частные производные функции:

а) 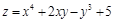; б) .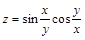

Решение.

а) .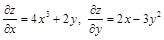

б) ,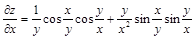

.

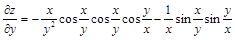Аналогично определяются производные функции трех и более переменных.

Определение 4. Частные дифференциалы определяются как главные части частных приращений функции:

.

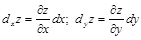Определение 5. Полным дифференциалом функции (или дифференциалом) 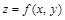называют сумму ее частных дифференциалов, т.е.

.

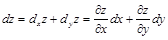Определение 6.Функция 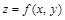называется дифференцированной в точке 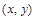, если ее полное приращение имеет вид 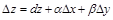, где 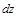– полный дифференциал функции, 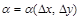, 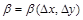– бесконечно малые при .

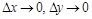Таким образом, дифференциал функции нескольких переменных, как и в случае функции одной переменной, есть главная (линейной относительно 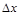и 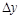) часть полного приращения.

Геометрическое смысл дифференциала заключается в том, что 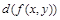является приращением аппликаты касательной плоскости к поверхности одной переменной, и базируется на равенстве .

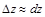Полный дифференциал функции применяют при приближенных вычислениях значений функций при условии 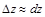, в развернутом ви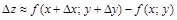де:

, где ,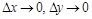

или

.

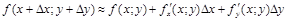Пример 3.Найти полный дифференциал функции .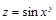

Решение. Найдем частные производные функции: