Общая схема исследования функции и построение графиков

Прежде чем построить график функции, необходимо провести исследования функции, а именно:

1.Найти область существования функции.

2.Найти точки пересечения графика с координатными осями, интервалы знакопостоянства функции.

3.Исследовать функцию на периодичность, четность и нечетность.

4.Найти точки разрыва функции и исследовать их характер.

5.Исследовать функцию с помощью первой производной (экстремумы функции и интервалы монотонности).

6.Исследовать функцию с помощью второй производной (точки перегиба, интервалы выпуклости и вогнутости).

7.Найти асимптоты графика функции.

8.На основе проведенного исследования заполнить таблицу (не обязательно) и построить график функции.

Пример 1. Исследовать и построить график функции

.

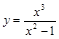Решение

Область определения функции

Заданная функция дробно-рациональная, поэтому она не существует в точках, где знаменатель равняется нулю, 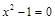, откуда .

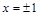Итак, область существования функции есть объединение множеств

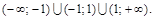
Точки пересечения графика с осями координат

а) Пусть у = 0 , тогда х = 0.

б) Пусть х = 0 , тогда у = 0.

Итак, график пересекает координатные оси в точке (0; 0), т.е. график проходит через начало координат.

Периодичность функции

Функция непериодическая.

Четность, нечетность функции

,

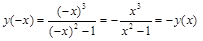функция нечетная, т.е. график симметричен началу координат.

Точки разрыва функции, характер их разрыва

Точками разрыва являются точки х = 1, х = –1. Исследуем их характер, найдем односторонние пределы:

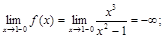
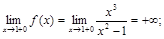
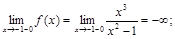
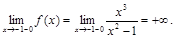
Итак, 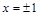— есть точки разрыва второго рода.

Прямые 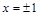— являются вертикальными асимптотами.

Исследование функции с помощью первой производной

а) Найдем :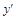

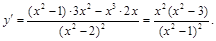
б) Найдем точки экстремума, решив уравнение:

.

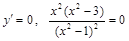Итак, ­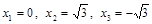– стационарные точки.

б) Найдем интервалы возрастания, убывания функции, решив неравенство .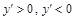

Разложив на множители и использовав метод интервалов, имеем:

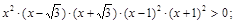
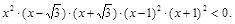
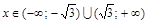Итак, при функция возрастает.

–1

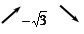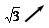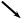При 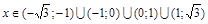функция убывает.

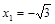— точка max,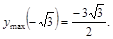

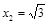— точка min,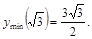

Исследование функции с помощью второй производной.

а) Найдем :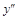

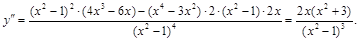
б) Решим неравенство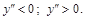

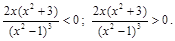
Сократив на положительный множитель, получим:

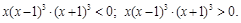
С помощью метода интервалов имеем:

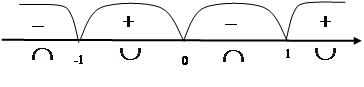Итак, при 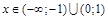кривая выпуклая.

При 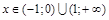кривая вогнутая.

в) Находим точки перегиба.

Решим уравнение 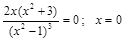– точка перегиба, т.к. при прохождении через точку х = 0 производная 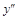меняет знак с + на –.

8. Находим наклонную асимптоту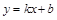

Вычисляем:

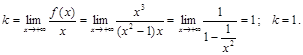
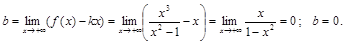
Уравнение наклонной асимптоты: .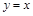

9. Для наглядности заполняем таблицу:

х		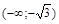-	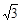	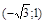-1	(-1;0)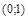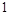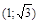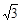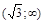
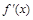	+		–	не сущ.	–		–	не сущ.	–		+
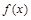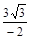	↗		↘	не сущ.	↘		↘	не сущ.	↘		↗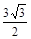
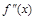	–		–		+	т. перегиба	–		+		+
			)		(		)		(		(

С помощью таблицы строим график функции

Примеры использования дифференциального исчисления в экономических задачах

Максимизация прибыли

Максимизация прибыли является одним из главных критериев деятельности производственных и коммерческих структур. Известно, что прибыль 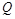является некоторой функцией от объема реализации х

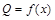
Пример 1. Фирме известно соотношение между еженедельной продажей продукции х и еженедельной прибылью Q (в экю), в виде функции

.

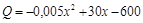Фирма стремится получить максимальную прибыль. Найдем эту прибыль.

Решение. Нетрудно видеть, что задача получения максимальной прибыли сводится к нахождению максимума функции 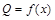. Для этого найдем производную Q по переменной х

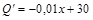
В точке максимума 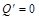, следовательно

.

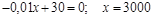Проверим, что при еженедельной продаже продукции 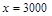еженедельная прибыль Q будет максимальной. Действительно, найдем вторую производную от функции Q (1)

,

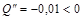а это и есть условия максимума.

Следовательно, точка 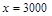является точкой локального максимума. Теперь найдем максимальную прибыль

.

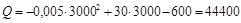Итак, для максимизации прибыли фирма должна еженедельно реализовывать 3000 единиц изготовленной продукции. При этом ее еженедельная прибыль будет максимальной и составит 44400 экю.

Прибыль Q, как известно, – это разность между доходом D (общая сумма денег, полученная от продажи выпускаемой продукции) и затратами (издержками) Е (общая стоимость затрат, связанных с производством и реализацией продукции):

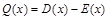, (1)

где х – количество произведенной и реализованной продукции. Следовательно, все эти величины являются функциями от объема продукции х. При этом

,

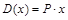где 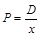– цена за единицу продукции х.

Заметим, что 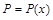– рыночная цена, которая монотонно уменьшается по мере увеличения объема выпускаемой продукции х, ведущего к насыщению рынка.

Наряду с величинами общей прибыли Q, общего дохода D и общих затрат (издержек производства) Е вводятся еще маргинальные (предельные) величины:

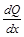– маргинальная прибыль;

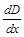– маргинальный доход;

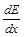– маргинальные затраты (издержки).

Тогда условие максимума прибыли эквивалентно условию равенства маргинального дохода и маргинальных затрат. Действительно, из равенства (1) имеем

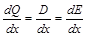. (2)

В точках максимума 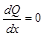. Тогда из (2) имеем

.

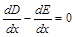Откуда

.

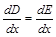Кроме того, в точках максимума должно выполняться условие

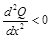. (3)

Из равенства (2) получим

,

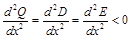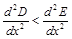. (4)

Пример 2. Известны общие затраты Е производства продукции и функция спроса на продукцию 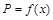(рыночная цена как функция объема спроса):

, .

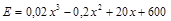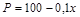Найти точку равновесия (Р*, х*), максимизирующую общую прибыль.

Решение. Найдем общий доход D(x)

.

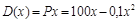Тогда маргинальный доход равен

.

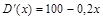Найдем маргинальные затраты

.

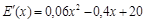Маргинальные затраты и маргинальный доход в точке максимума равны между собой, следовательно, имеем

,

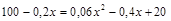откуда

; ;

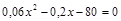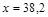(значение х = –34 отбрасываем, т.к. оно не соответствует экономическому смыслу – объем продукции всегда положителен). Проверим условие максимума (4) при х = 38,2.

.

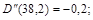
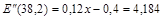Условие (4) выполняется.

Следовательно, х = 38,2 дает максимум прибыли.

Цена продукции

.

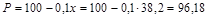Прибыль

.
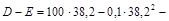
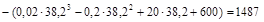