Физический смысл производной
Под физическим смыслом производной понимают скорость изменения функции в данной точке. Например:
1) при движении тела скорость 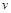 в данный момент времени
в данный момент времени 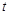 есть производная от пути
есть производная от пути 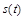 :
: 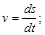
2) при вращательном движении твердого тела вокруг оси 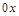 угловая скорость
угловая скорость 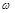 в данный момент времени
в данный момент времени 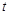 есть производная от угла поворота:
есть производная от угла поворота: 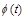 :
: 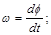
3) при охлаждении тела скорость охлаждения в момент времени 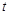 есть производная от температуры:
есть производная от температуры: 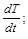
4) теплоемкость С для данной температуры 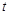 есть производная от количества тепла
есть производная от количества тепла 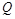 :
: 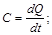
5) при нагревании стержня коэффициент линейного расширения 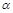 при данном значении температуры
при данном значении температуры 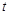 есть производная от длины
есть производная от длины 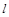 :
: 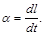
Пример 2. Найти скорость точки, движение которой описывается уравнением 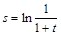 , в конце третьей секунды.
, в конце третьей секунды.
Решение.Скорость определяется по формуле
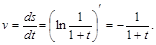
Когда 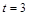 , имеем
, имеем 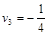 (м/с).
(м/с).
Дифференциал функции
Дифференциал функции, как и производная, применяется при решении ряда практических задач, в частности в приближенных вычислениях.
Определение 1. Дифференциалом функции 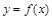 в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается
в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается 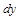 (или
(или 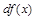 )
)
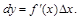 (1)
(1)
Дифференциал 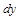 называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т.е. дифференциал функции
называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т.е. дифференциал функции 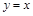 .
.
Так как 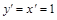 , то, согласно формуле (1), имеем
, то, согласно формуле (1), имеем 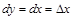 , т.е. дифференциал независимой переменной равен приращению этой переменной:
, т.е. дифференциал независимой переменной равен приращению этой переменной: 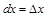 .
.
Поэтому формулу (1) можно записать так:
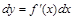 (2)
(2)
откуда
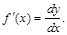
Основные свойства дифференциала
Основные теоремы о дифференциалах легко получить, используя связь дифференциала и производной функции 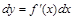 и соответствующие теоремы о производных.
и соответствующие теоремы о производных.
Например, так как производная функции 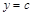 равна нулю, то дифференциал постоянной величины равен нулю:
равна нулю, то дифференциал постоянной величины равен нулю:
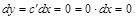 . (3)
. (3)
Теорема 1. Дифференциалы суммы, произведения и частного двух дифференцируемых функций определяются следующими формулами
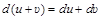 , (4)
, (4)
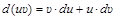 , (5)
, (5)
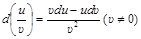 . (6)
. (6)
Теорема 2. Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента.
Пример 1.Найти дифференциал функции 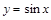 .
.
Решение. 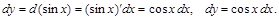
Пример 2.Найти дифференциал функции 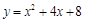 .
.
Решение. 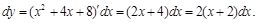
Применение дифференциала к приближенным вычислениям
При малых 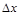 справедливая формула
справедливая формула 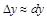 , т.е.
, т.е.
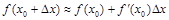 . (7)
. (7)
Данная формула широко применяется в вычислительной практике, так как дифференциал обычно находится значительно проще, чем приращение функции.
Пример 3.Вычислить приближенно с помощью дифференци-ала значение функции 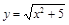 в точке
в точке 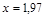 .
.
Решение.Ближайшая к 1,97 точка, у которой легко вычислить значение 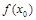 и
и 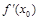 , – это точка
, – это точка 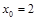 .
.
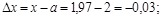
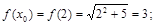
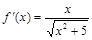 ,
, 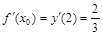 .
.
По формуле 2 имеем