Действия над последовательностями
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
КОНСПЕКТЫ ЛЕКЦИЙ
№ 2
| Содержание | ||
| 1. | Числовые последовательности. Примеры…………………………... | |
| 2. | Действия над последовательностями…………………………......... | |
| 3. | Ограниченные и монотонные последовательности……………….... | |
| 4. | Сходящаяся последовательность. Предел последовательности……... | |
| 5. | Бесконечно малая величина……… | |
| 6. | Свойства сходящихся последовательностей……………………….... | |
| 7. | Предельный переход в неравенствах…………………………………. | |
| 8. | Теоремы существования. Число 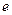 ……………………………. ……………………………. |
Лекция 2
Вещественная функция натурального аргумента – числовая последовательность. Подпоследовательность. Действия над последовательностями. Ограниченные и монотонные последовательности. Определение предела последовательности. Сходящиеся и фундаментальные последовательности. Теорема Коши.
Числовые последовательности. Примеры
Рассмотрим функции 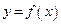 , заданные на множестве натуральных чисел
, заданные на множестве натуральных чисел 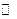 . Такие функции называются функциями натурального аргумента.
. Такие функции называются функциями натурального аргумента.
Множество значений функции натурального аргумента – 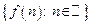 называется числовой последовательностью (или последовательностью), а каждое значение
называется числовой последовательностью (или последовательностью), а каждое значение 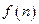 этой функций – членом
этой функций – членом
числовой последовательности. Так как числовая последовательность является конкретным и часто используемым понятием, то удобно для неё использовать иное обозначение, а именно, вместо 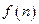 будем писать
будем писать 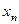 :
: 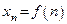 .
.
Члены числовой последовательности располагаются в порядке возрастания аргумента
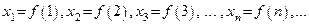 ,
,
при этом
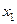 – первый член последовательности;
– первый член последовательности;
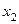 – второй член последовательности;
– второй член последовательности;
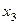 – третий член последовательности;
– третий член последовательности;
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
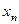 –
– 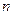 -й или общий член последовательности.
-й или общий член последовательности.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Последовательность 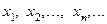 коротко можно обозначать
коротко можно обозначать 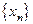 .
.
Последовательность 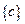 , где
, где 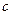 произвольное вещественное число, называется стационарной последовательностью или постоянной величиной.
произвольное вещественное число, называется стационарной последовательностью или постоянной величиной.
Пусть 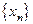 – произвольная последовательность. Для всякой последовательности натуральных чисел
– произвольная последовательность. Для всякой последовательности натуральных чисел 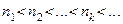 последовательность
последовательность 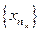 называется подпоследовательностью последовательности
называется подпоследовательностью последовательности 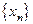 .
.
Пример 1.1. 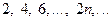 или
или 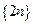 .
.
Пример 1.2. 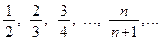 или
или 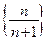 .
.
Пример 1.3. 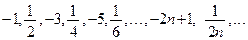 или
или 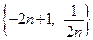 .
.
Пример 1.4. 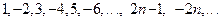
или 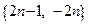 .
.
Пример 1.5. 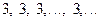 или
или 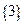 .
.
Действия над последовательностями
Пусть даны последовательности 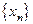 и
и 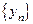 .
.
Произведением последовательности
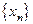 или
или 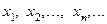
на число 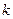 называется последовательность
называется последовательность
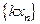 или
или 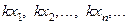 .
.
Суммой двух последовательностей 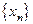 и
и 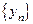 называется последовательность
называется последовательность
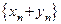 или
или 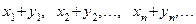 .
.
Разностью двух последовательностей 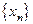 и
и 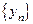 называется последовательность
называется последовательность
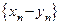 или
или 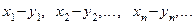 .
.
Произведением двух последовательностей 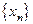 и
и 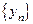 называется последовательность
называется последовательность
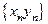 или
или 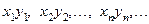 .
.
Частным двух последовательностей 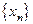 и
и 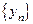 называется последовательность
называется последовательность
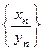 или
или 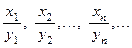 ,
,
при этом предполагается, что либо все 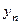 отличны от нуля, либо все
отличны от нуля, либо все 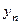 отличны от нуля начиная с некоторого номера (в этом случае частное определяется с этого номера).
отличны от нуля начиная с некоторого номера (в этом случае частное определяется с этого номера).
