Обыкновенные дифференциальные уравнения первого порядка
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ
ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧЕРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
МАГНИТОГОРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ ИМ. Г. И. НОСОВА
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Учебное пособие для студентов заочной формы обучения
Магнитогорск
Составители:М.В.Быкова
Н.А.Квасова
Н.И.Кимайкина
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Учебное пособие по дисциплине «Математика» для студентов заочной формы обучения
Магнитогорск : ФГ БОУ ВПО МГТУ, 70стр.
Учебное пособие рекомендуется студентам всех специальностей, обучающимся на заочном факультете.
В работе рассмотрены все типы обыкновенных дифференциальных уравнений первого порядка, линейные дифференциальные уравнения высших порядков, системы дифференциальных уравнений. Приведены примеры решения уравнений, задачи для самостоятельной работы, контрольные вопросы, справочные таблицы.
Быкова М.В.
Квасова Н.А.
Кимайкина Н.И.
Учебное пособие для студентов заочного обучения включает вопросы по теме «Дифференциальные уравнения», в качестве учебника предлагается «Вся высшая математика» (1). Литература (2), (3) поможет применить теорию к решению задач. При изучении теории полезно составлять для себя справочные таблицы. Это поможет систематизировать основные положения теории дифференциальных уравнений, а в дальнейшем эти таблицы могут быть использованы при изучении других дисциплин (физики, механики). Как образец таких таблиц в методической разработке предлагаются справочные таблицы 1-2 (могут быть использованы и другие варианты).
Далее следует приступить к разбору типовых задач по теме, которые предлагаются в пособии. Это поможет закрепить теоретические знания и применить их к решению задач.
Для проверки степени усвоения теоретического материала и качества составления таблиц в методической разработке предлагаются задачи для самостоятельной работы. К ним прилагаются ответы.
Дифференциальные уравнения в приложениях математики к техническим наукам
Введение
В приложениях математики к техническим наукам дифференциальные уравнение занимают важное место.
Пусть перед инженерами стоит задача изучить некоторый производственный процесс. Изучение начинается с формализации объекта, с построения математической модели: выделяются наиболее существенные черты, параметры и свойства изучаемого процесса, и затем описываются с помощью математических уравнений.
После того как построена математическая модель изучаемого процесса, то есть задаче придана математическая форма, можно для её решения применить математические методы.
При исследовании какого либо технического, химического, физического процессов приходится устанавливать функциональную зависимость между переменными параметрами рассматриваемого процесса. Большинство таких задач приводит к дифференциальным уравнениям.
Пусть  -это уравнение связывает независимую переменную x и производную функции y. Решив уравнение, мы установим связь между переменными x и y (где y-искомая функция, x-её аргумент).
-это уравнение связывает независимую переменную x и производную функции y. Решив уравнение, мы установим связь между переменными x и y (где y-искомая функция, x-её аргумент).
1)Рассмотрим прямолинейное движение тела. Оно характеризуется расстоянием X на прямой, пройденным телом за время t , то есть: 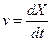 или
или
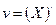
2)Согласно второму закону Ньютона  , где F– сила, действующая на движущееся тело; m - масса тела;
, где F– сила, действующая на движущееся тело; m - масса тела;  - ускорение.
- ускорение.
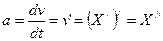
Сила, действующая на тело и сообщающая ему ускорение, может быть постоянной или меняться с течением времени.
а) F=const при свободном падении тела. Из
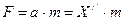 выразим
выразим  или
или  . Уравнение принимает вид:
. Уравнение принимает вид: 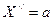 или
или 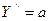
б) Движение по инерции: F=0. Тогда из
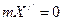 получаем
получаем  или
или 
в) Движение в среде с вязким трением: сила направлена против движения и прямо пропорциональна скорости 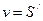 :
:  или
или  или
или  или
или  , где
, где 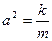
г) Движение под действием упругой силы: сила пропорциональна отклонению и направлена против движения (например, шарик на пружине) 
 или
или  , т.е.
, т.е. 
Можно привести и другие примеры из химии, биологии, социологии, где встречаются уравнения, содержащие неизвестную функцию вместе с её производными. Такие уравнения называются дифференциальными.
Мы будем рассматривать обыкновенные дифференциальные уравнения. Неизвестная функция в этих уравнениях зависит только от одной переменной. Причем, одно и тоже дифференциальное уравнение может описывать различные явления и процессы.
Так уравнению  удовлетворяют: 1) механическое движение под действием упругой силы (например, движение шарика на пружине, здесь
удовлетворяют: 1) механическое движение под действием упругой силы (например, движение шарика на пружине, здесь 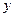 - величина отклонения от положения равновесия;
- величина отклонения от положения равновесия; 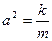 , m – масса шарика; k – коэффициент упругости пружины); 2) величина тока в контуре, состоящем из конденсатора емкости С и катушки индуктивности L, при этом
, m – масса шарика; k – коэффициент упругости пружины); 2) величина тока в контуре, состоящем из конденсатора емкости С и катушки индуктивности L, при этом  .
.
Примеры решения задач
Задача 1.1.Задача о чайнике.
За какое время тело , нагретое до 100  охладится до 25
охладится до 25  в комнате с температурой 20
в комнате с температурой 20  , если до 60
, если до 60  оно охлаждается за 10 минут.
оно охлаждается за 10 минут.
Решение:
Пусть через t минут температура тела будет T.
По закону Ньютона скорость охлаждения тела пропорциональна разности температур. 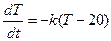 ,
,
здесь k-пока неизвестный коэффициент пропорциональности.
Разделим переменные в дифференциальном уравнении и проинтегрируем его:
 -общий интеграл уравнения.
-общий интеграл уравнения.
Используя начальные условия, найдем С.
 :
:
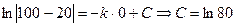 , т.е.
, т.е.  -частное решение.
-частное решение.
Найдем k:

при t=10мин. 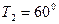 , тогда
, тогда  ;
; 

Ответ: за 40 мин. Чайник ,нагретый до 100  охладится до 25
охладится до 25  .
.
Задача 1.2. О полете тела, брошенного под углом к горизонту.
Пусть тело брошено под углом 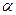 к горизонту с начальной скоростью
к горизонту с начальной скоростью  . Вывести уравнение движения тела, пренебрегая силами сопротивления. (Рис.1).
. Вывести уравнение движения тела, пренебрегая силами сопротивления. (Рис.1).

В произвольном положении на тело М массой m действует сила его веса  . В соответствии со вторым законом Ньютона дифференциальные уравнения движения в проекциях на оси OX и OY запишутся в виде:
. В соответствии со вторым законом Ньютона дифференциальные уравнения движения в проекциях на оси OX и OY запишутся в виде:
 или
или  (1.1)
(1.1)
Начальные условия движения тела
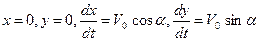 при
при  (1.2)
(1.2)
Интегрируя уравнения (1) и учитывая начальные условия (2) получим уравнения движения тела:
 (1.3)
(1.3)
Это параметрические уравнения параболы. Избавимся от параметра t и получим
 (1.4)
(1.4)
Из уравнений (1.3),(1.4) можно сделать ряд выводов о характере движения брошенного тела.
1)Найти время полета тела до его падения на землю.
Найдем t, при котором  :
:

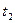 -искомое время полета.
-искомое время полета.
2)Найти расстояние 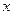
 полета тела по горизонтали:
полета тела по горизонтали:
Для этого вычислим x при  .Подставим в уравнение
.Подставим в уравнение  значение
значение 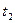 .
.

Расстояние x будет наибольшим при  и тогда
и тогда 
Обыкновенные дифференциальные уравнения первого порядка.
Основные понятия.
Определение 2.1.Обыкновенным дифференциальным уравнением первого порядка называется уравнение, связывающее независимую переменную x, искомую функцию  и её производную
и её производную  , то есть уравнение вида
, то есть уравнение вида  . (2.1)
. (2.1)
Определение 2.2.Решением дифференциального уравнения (2.1) называется такая дифференцируемая функция  , которая при подстановке в уравнение обращает его в тождество.
, которая при подстановке в уравнение обращает его в тождество.
Примеры: a) Проверим, является ли функция  решением дифференциального уравнения
решением дифференциального уравнения 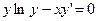 ?
?
 и
и  подставим в уравнение
подставим в уравнение 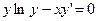 .
.
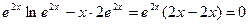 , т.е. функция
, т.е. функция  - является решением уравнения.
- является решением уравнения.
b) Докажем, что функция  , где С=const, является решением уравнения
, где С=const, является решением уравнения  .
.
Действительно, подставим в уравнение  и
и  ,
,
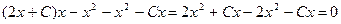
т.е. функция  является решением уравнения.
является решением уравнения.
Это уравнение имеет множество решений, т.к. С может принимать любые значения.
Рассмотрим дифференциальные уравнения первого порядка  , которые можно разрешить относительно
, которые можно разрешить относительно  , то есть
, то есть
 (2.2)
(2.2)
или  (2.3)
(2.3)
Уравнение (2.3) приведем к виду (2.2): Пусть 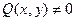 , тогда
, тогда 
Примеры дифференциальных уравнений первого порядка вида (2.2) и (2.3):
a)  ,
,  ;
;
b)  ,
,  ;
;
c)  ,
, 
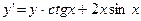 ;
;
d)  ,
,  .
.
Теорема Коши (теорема существования и единственностирешения дифференциального уравнения первого порядка.  ).
).
Если функция  и её частная производная
и её частная производная  определены и непрерывны в некоторой области D изменения переменных x и y, то данное уравнение
определены и непрерывны в некоторой области D изменения переменных x и y, то данное уравнение  имеет единственное решение
имеет единственное решение  , удовлетворяющее условию
, удовлетворяющее условию  , для всех точек
, для всех точек  , (2.4).
, (2.4).
Условия (2.4) (или  при
при  ) называют начальными условиями.
) называют начальными условиями.
Уравнение  (2.2) вместе с начальными условиями
(2.2) вместе с начальными условиями  (2.4) называют Задачей Коши.
(2.4) называют Задачей Коши.
Точки плоскости, в которых не выполняются условия теоремы Коши, называются особыми точками дифференциального уравнения. В этих точках  и
и  терпят разрыв.
терпят разрыв.
Определение 2.3. Общим решением дифференциального уравнения  в некоторой области D называется функция
в некоторой области D называется функция  , которая:
, которая:
a) является решением уравнения при любом С=const ;
b) при любых начальных условиях  ,где
,где  существует единственное значение С=С
существует единственное значение С=С 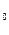
 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 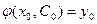 .
.
Определение2.4.Частным решением уравнения  в области D называется функция , которая получается из общего решения
в области D называется функция , которая получается из общего решения  при С=С
при С=С 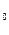
 .
.
Общее решение может быть получено в неявном виде  , тогда оно называется общим интегралом.
, тогда оно называется общим интегралом.
